We have now talked at length about the basics of inference on the mean of quantitative data.  What if the variable we are interested in is categorical?  We cannot calculate means, variances, and the like for categorical data.  However, we can count the number of individuals that have a characteristic we are interested in and divide by the total number in our population to get the population proportion (p).

Suppose a poll suggested the US President’s approval rating is 45%. We would consider 45% to be a point estimate of the approval rating we might see if we collected responses from the entire population. This entire-population response proportion is generally referred to as the parameter of interest. When the parameter is a proportion, it is often denoted by p, and we often refer to the sample proportion as ˆp (pronounced “p-hat”). Unless we collect responses from every individual in the population, p remains unknown, and we use ˆp as our estimate of p. The difference we observe from the poll versus the parameter is called the error in the estimate.

Understanding the Variability of a Proportion

Suppose we know the proportion of American adults who support the expansion of solar energy is p = 0.88, which is our parameter of interest. If we were to take a poll of 1000 American adults on this topic, the estimate would not be perfect, but how close might we expect the sample proportion in the poll would be to 88%? We want to understand, how does the sample proportion, ˆp, behave when the true population proportion is 0.88.  We can simulate responses we would get from a simple random sample of 1000 American adults, which is only possible because we know the actual support for expanding solar energy is 0.88. Here’s how we might go about constructing such a simulation:

1. There were about 250 million American adults in 2018. On 250 million pieces of paper, write “support” on 88% of them and “not” on the other 12%.
2. Mix up the pieces of paper and pull out 1000 pieces to represent our sample of 1000 American adults.
3. Compute the fraction of the sample that say “support”.

Any volunteers to conduct this simulation? Probably not. Running this simulation with 250 million pieces of paper would be time-consuming and very costly, but we can simulate it using technology.  In this simulation, one sample gave a point estimate of ˆp₁ = 0.894. We know the population proportion for the simulation was p = 0.88, so we know the estimate had an error of 0.894 − 0.88 = +0.014.  One simulation isn’t enough to get a great sense of the distribution of estimates we might expect in the simulation, so we should run more simulations. In a second simulation, we get ˆp₂ = 0.885, which has an error of +0.005. In another, ˆp₃ = 0.878 for an error of -0.002. And in another, an estimate of ˆp₄ = 0.859 with an error of -0.021. With the help of a computer, we’ve run the simulation 10,000 times and created a histogram of the results from all 10,000 simulations in the following figure:

This simulates the sampling distribution of the sample proportion. We can characterize this sampling distribution as follows:

• Center: The center of the distribution is 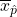 = 0.880, which is the same as the parameter. Notice that the simulation mimicked a simple random sample of the population, which is a straightforward sampling strategy that helps avoid sampling bias.
• Spread: The standard deviation of the distribution is 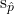= 0.010. When we’re talking about a sampling distribution or the variability of a point estimate, we typically use the term standard error rather than standard deviation, and the notation 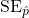is used for the standard error associated with the sample proportion.
• Shape: The distribution is symmetric and bell-shaped, and it resembles a normal distribution.

When the population proportion is p = 0.88 and the sample size is n = 1000, the sample proportion ˆp looks to give an unbiased estimate of the population proportion and resembles a normal distribution.  It looks as if we can apply the central limit theorem here too under the following conditions.

Conditions for the CLT for p

When observations are independent and the sample size is sufficiently large, the sample proportion ˆp will tend to follow a normal distribution with parameters:

In order for the Central Limit Theorem to hold, the sample size is typically considered sufficiently large when np ≥ 10 and n(1 − p) ≥ 10*.  Hopefully you see some similarity here to the normal approximation to the binomial which is one of the underlying theories here.

*Note: Some resources may use 5 here but 10 is safer.

What if we do not meet these conditions? Consider the following distributions and see if any patterns emerge:

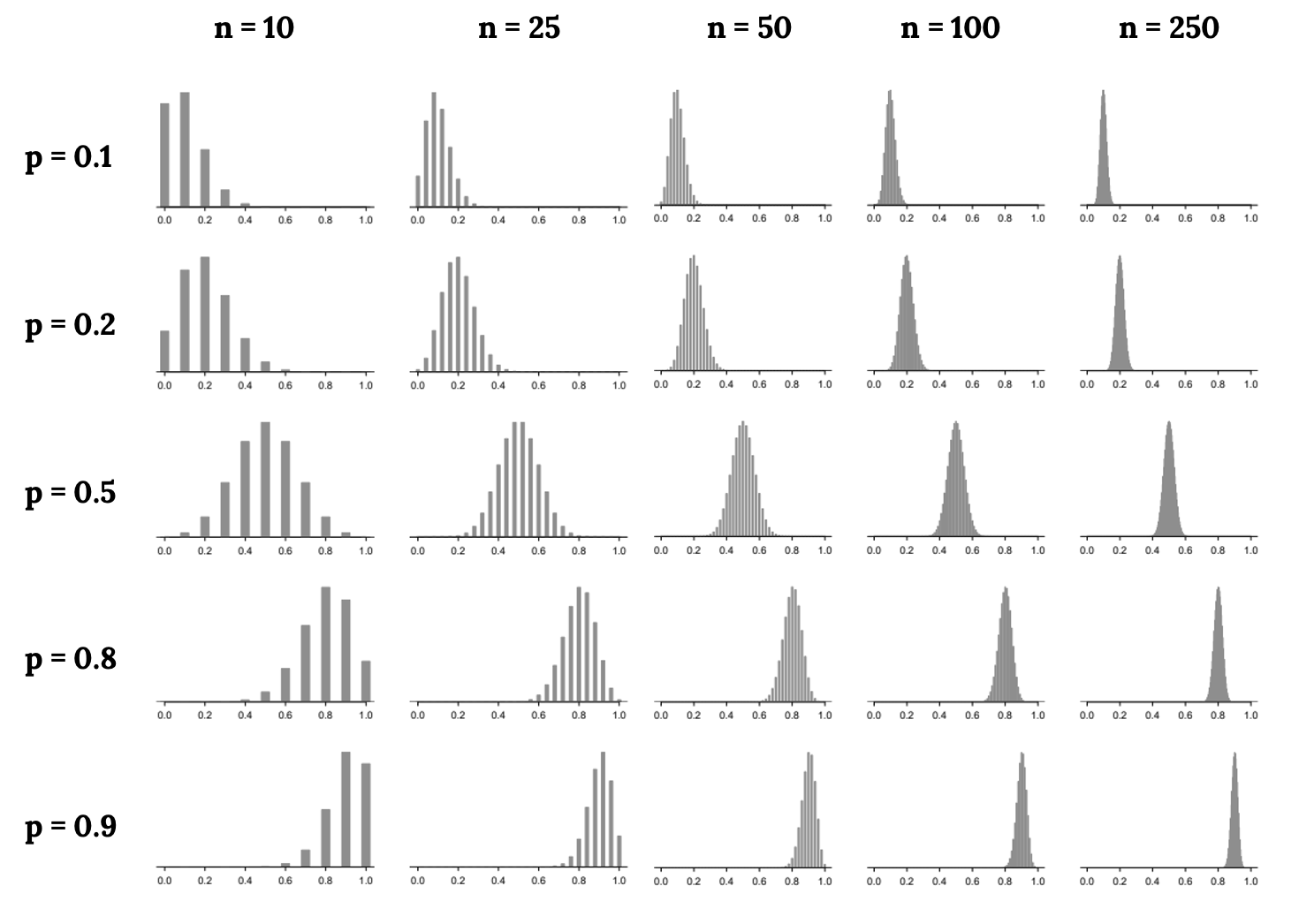
From these distributions we can see some patterns:

1. When either np or n(1 − p) is small, the distribution is more discrete, i.e. not continuous.
2. When np or n(1 − p) is smaller than 10, the skew in the distribution is more noteworthy.
3. The larger both np and n(1−p), the more normal the distribution. This may be a little harder to see for the larger sample size in these plots as the variability also becomes much smaller.
4. When np and n(1 − p) are both very large, the distribution’s discreteness is hardly evident, and the distribution looks much more like a normal distribution.

In regards to how the mean and standard error of the distributions change:

1. The centers of the distribution are always at the population proportion, p, that was used to generate the simulation. Because the sampling distribution of ˆp is always centered at the
   population parameter p, it means the sample proportion ˆp is unbiased when the data are independent and drawn from such a population.
2. For a particular population proportion p, the variability in the sampling distribution decreases as the sample size n becomes larger. This will likely align with your intuition: an estimate based on a larger sample size will tend to be more accurate.
3. For a particular sample size, the variability will be largest when p = 0.5. The differences may be a little subtle, so take a close look. This reflects the role of the proportion p in the standard error formula. The standard error is largest when p = 0.5.

At no point will the distribution of ˆp look perfectly normal, since ˆp will always be take discrete values (x/n). It is always a matter of degree, and we will use the standard success-failure condition with minimums of 10 for np and n(1 − p) as our guideline within this book.

Image References

Figure 7.6: Kindred Grey (2020). “Figure 7.4.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_7.4.png

Figure 7.7: Kindred Grey via Virginia Tech (2020). “Figure 7.5” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_7.5.png . Adaptation of Figures 5.4 and 5.5 from OpenIntro Introductory Statistics (2019) (CC BY-SA 3.0). Retrieved from https://www.openintro.org/book/os/