2.2 Displaying and Describing Categorical Data
Descriptive Statistics for Categorical Data
Categorical data is typically more straightforward to work with. Recall descriptive statistics consists of visual and numerical methods. We usually start with visual methods and then move into numerical.
Graphical Methods for Categorical Data
Below are tables comparing the number of part-time and full-time students at De Anza College and Foothill College enrolled for the spring 2010 quarter. The tables display counts (frequencies) and percentages or proportions (relative frequencies). The percent columns make comparing the same categories in the colleges easier. Displaying percentages along with the numbers is often helpful, but it is particularly important when comparing sets of data that do not have the same totals, such as the total enrollments for both colleges in this example. Notice how much larger the percentage for part-time students at Foothill College is compared to De Anza College.
| De Anza College | Foothill College | |||||
|---|---|---|---|---|---|---|
| Number | Percent | Number | Percent | |||
| Full-time | 9,200 | 40.9% | Full-time | 4,059 | 28.6% | |
| Part-time | 13,296 | 59.1% | Part-time | 10,124 | 71.4% | |
| Total | 22,496 | 100% | Total | 14,183 | 100% | |
Tables are a good way of organizing and displaying data. But graphs can be even more helpful in understanding the data. There are no strict rules concerning which graphs to use. Two graphs that are used to display categorical data are pie charts and bar graphs.
Pie Charts
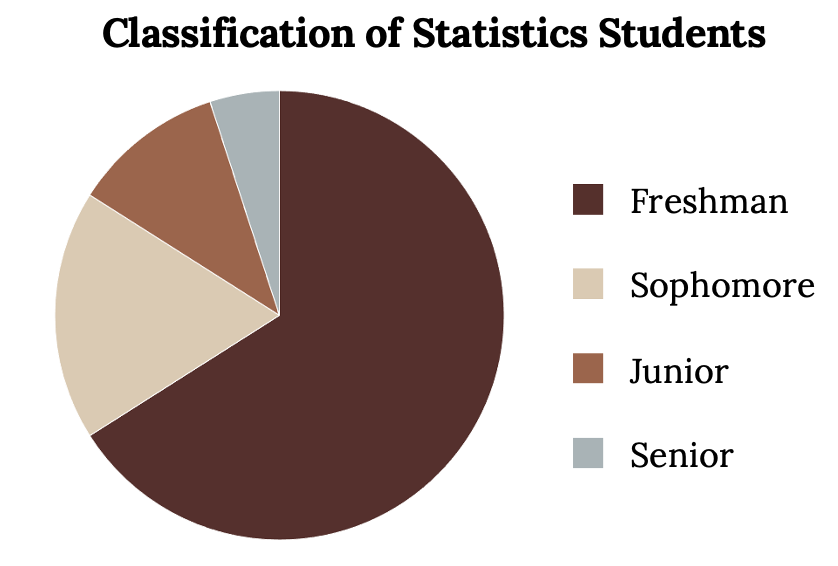
In a pie chart, categories of data are represented by wedges in a circle and are proportional in size to the percent of individuals in each category. Suppose a statistics professor collects information about the classification of her students as freshmen, sophomores, juniors, or seniors. The data she collects are summarized in the pie chart below.
Bar Graphs
Bar graphs consist of bars that are separated from each other. The length of the bar for each category is proportional to the number or percent of individuals in each category. The bars can be rectangles or they can be rectangular boxes (used in three-dimensional plots), and they can be vertical or horizontal. The bar graph shown in the figure below has age groups represented on the x-axis and proportions on the y-axis.
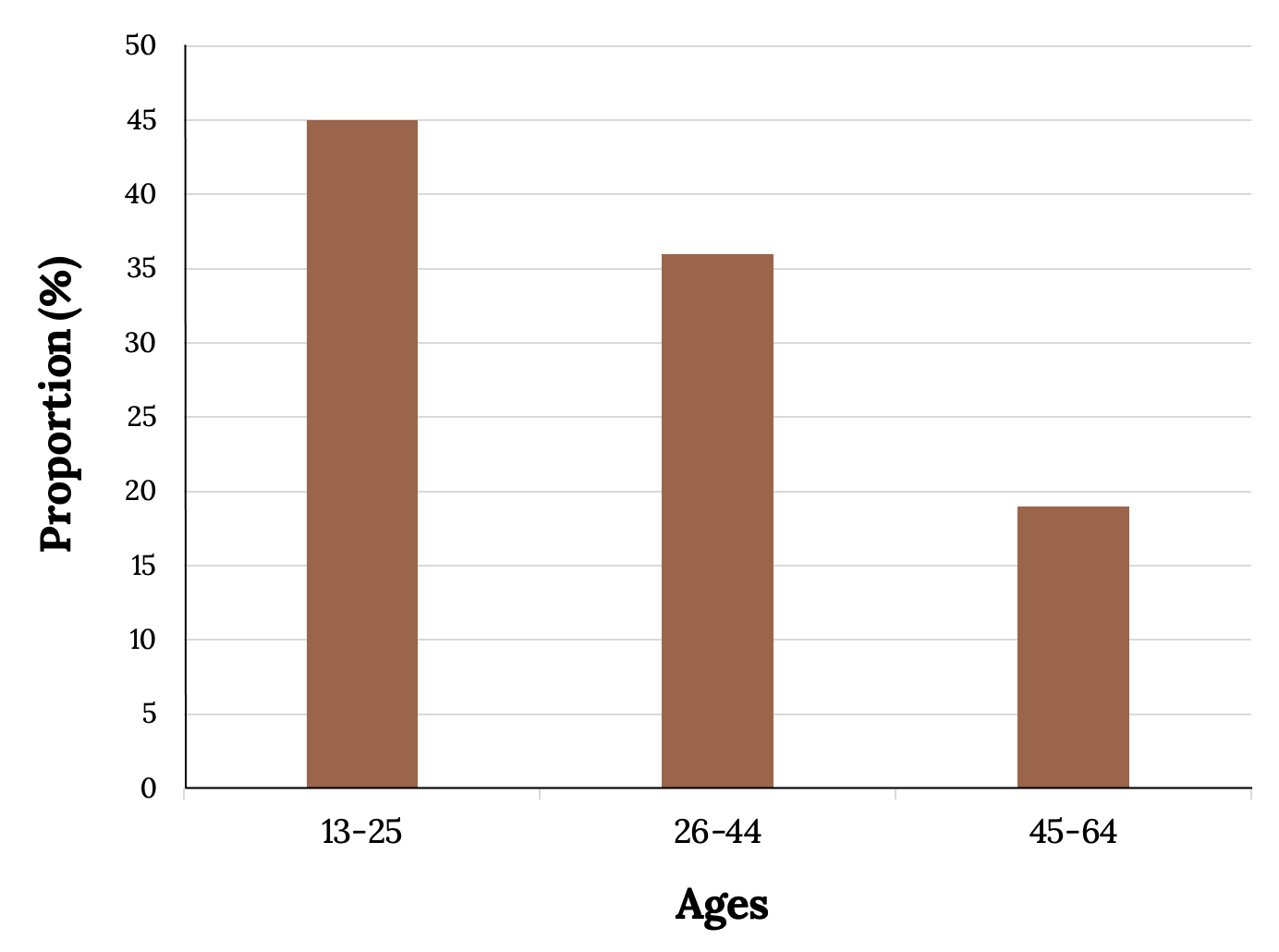
By the end of 2011, Facebook had over 146 million users in the United States. The figure below shows three age groups, the number of users in each age group, and the proportion (%) of users in each age group. Construct a bar graph using this data.
| Age groups | Number of Facebook users | Proportion (%) of Facebook users |
|---|---|---|
| 13–25 | 65,082,280 | 45% |
| 26–44 | 53,300,200 | 36% |
| 45–64 | 27,885,100 | 19% |
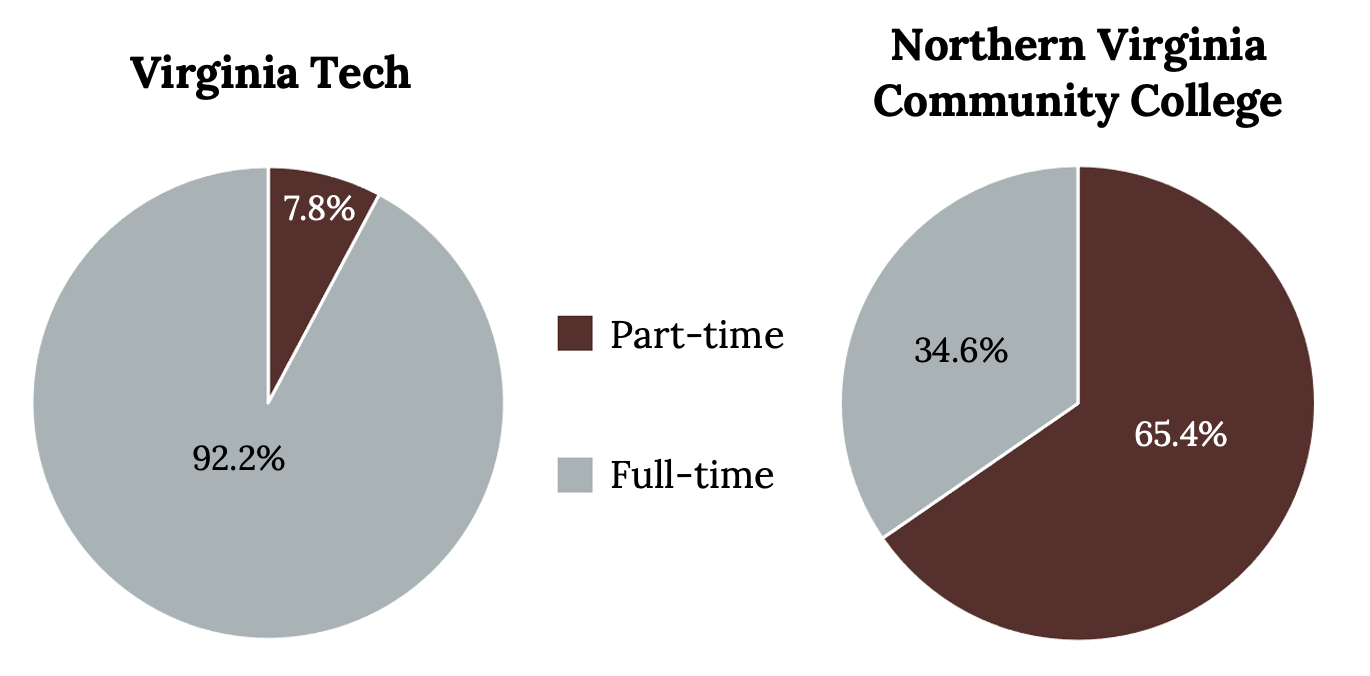
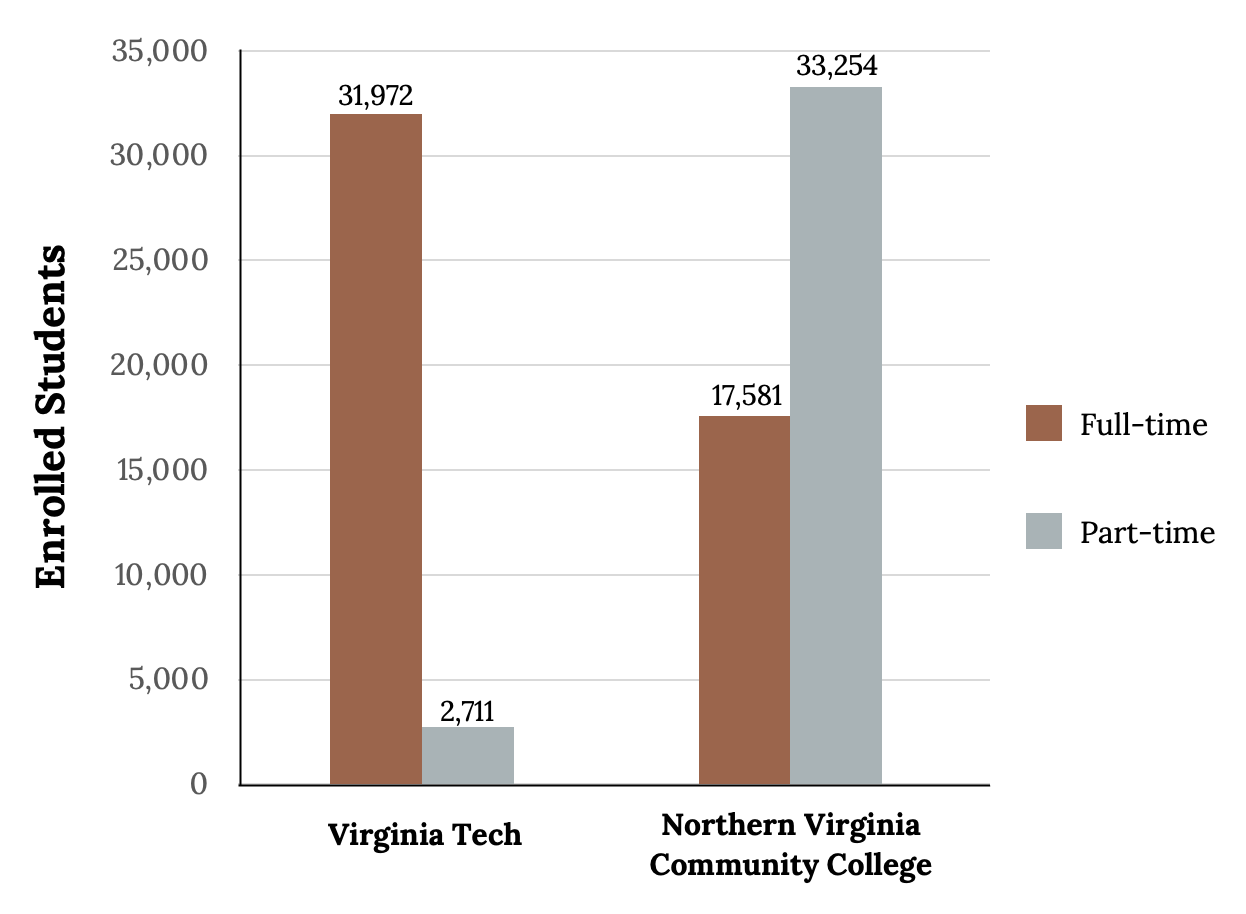
Pie vs. Bar Charts
It is a good idea to look at a variety of graphs to see which is the most helpful in displaying the data. We might make different choices of what we think is the “best” graph depending on the data and the context. Our choice also depends on what we are using the data for. Look at the following plots (pie or bar) and think about which you think displays the comparisons better:
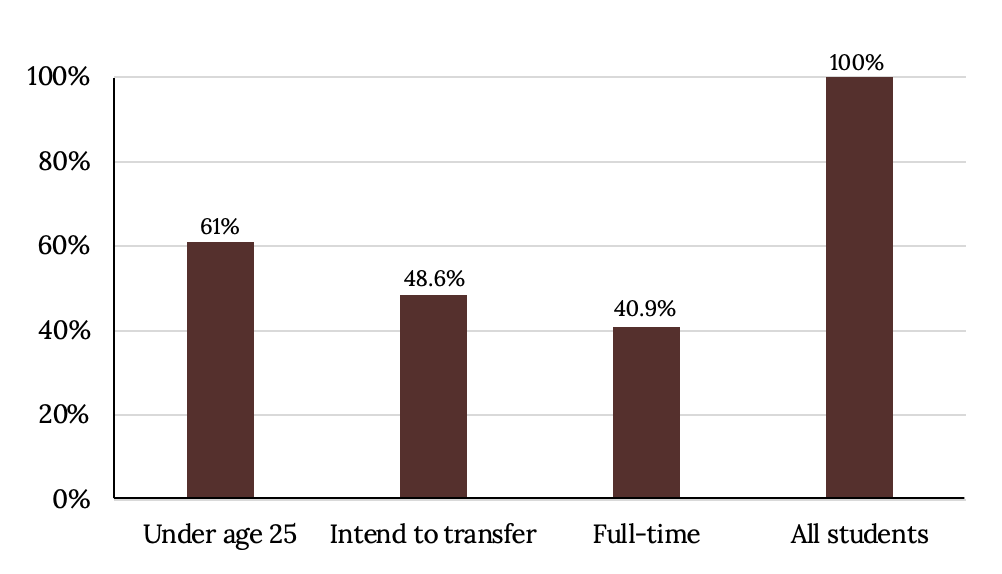
Percentages That Add to More (or Less) than 100%
| Characteristic/Category | Percent |
|---|---|
| Full-Time Students | 40.9% |
| Students who intend to transfer to a 4-year educational institution | 48.6% |
| Students under age 25 | 61.0% |
| TOTAL | 150.5% |
Omitting Categories/Missing Data
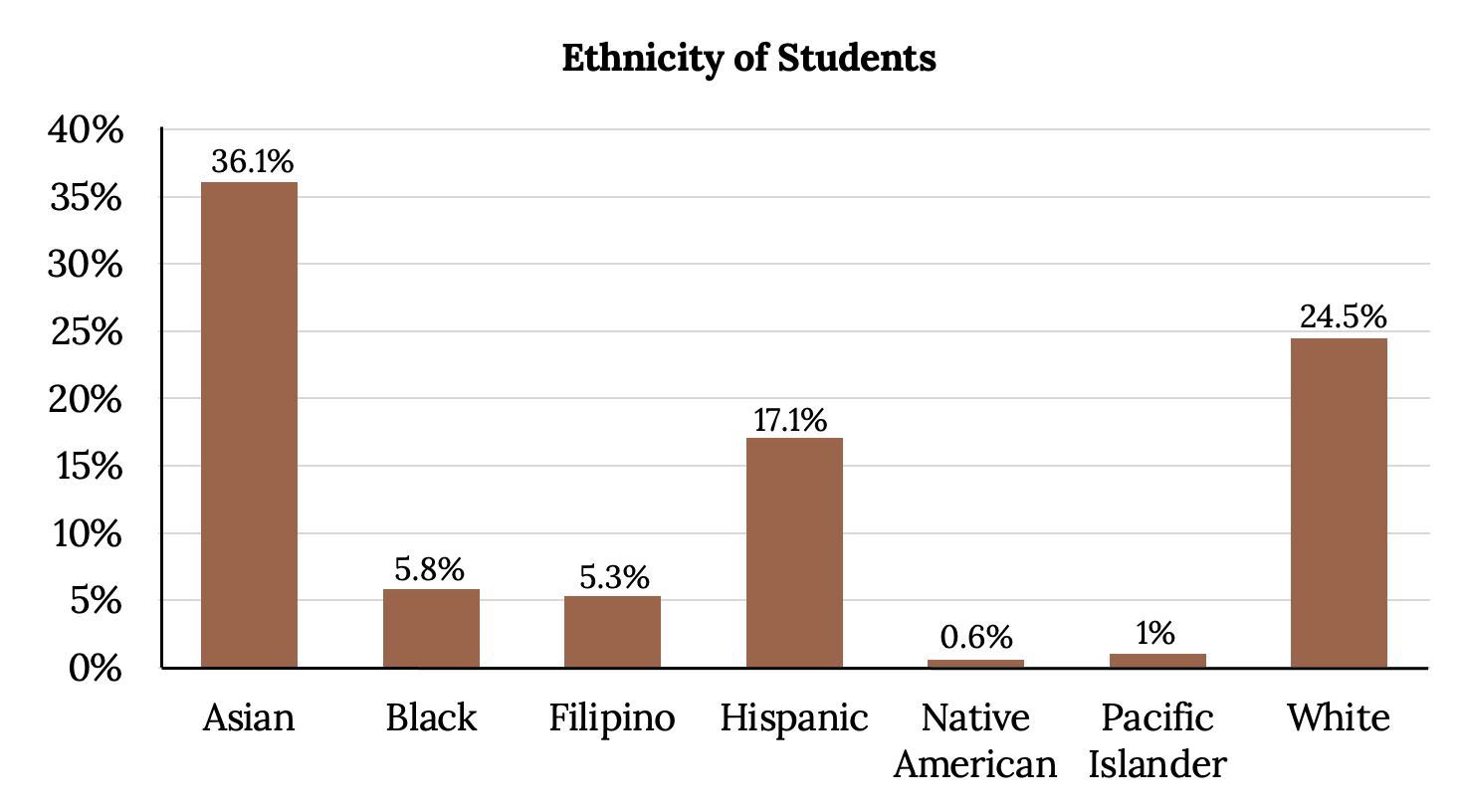
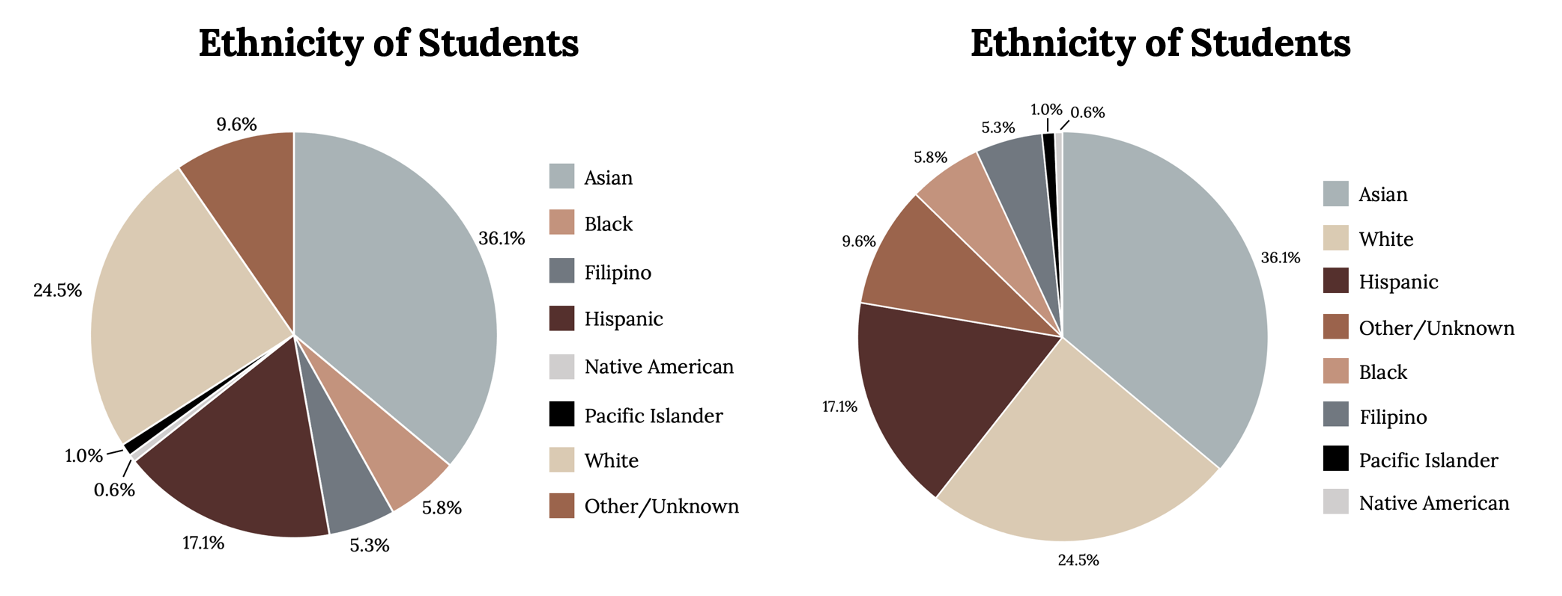
The table displays Ethnicity of Students but is missing the “Other/Unknown” category. This category contains people who did not feel they fit into any of the ethnicity categories or declined to respond. Notice that the frequencies do not add up to the total number of students. In this situation, create a bar graph and not a pie chart.
| Frequency | Percent | |
|---|---|---|
| Asian | 8,794 | 36.1% |
| Black | 1,412 | 5.8% |
| Filipino | 1,298 | 5.3% |
| Hispanic | 4,180 | 17.1% |
| Native American | 146 | 0.6% |
| Pacific Islander | 236 | 1.0% |
| White | 5,978 | 24.5% |
| TOTAL | 22,044 out of 24,382 | 90.4% out of 100% |
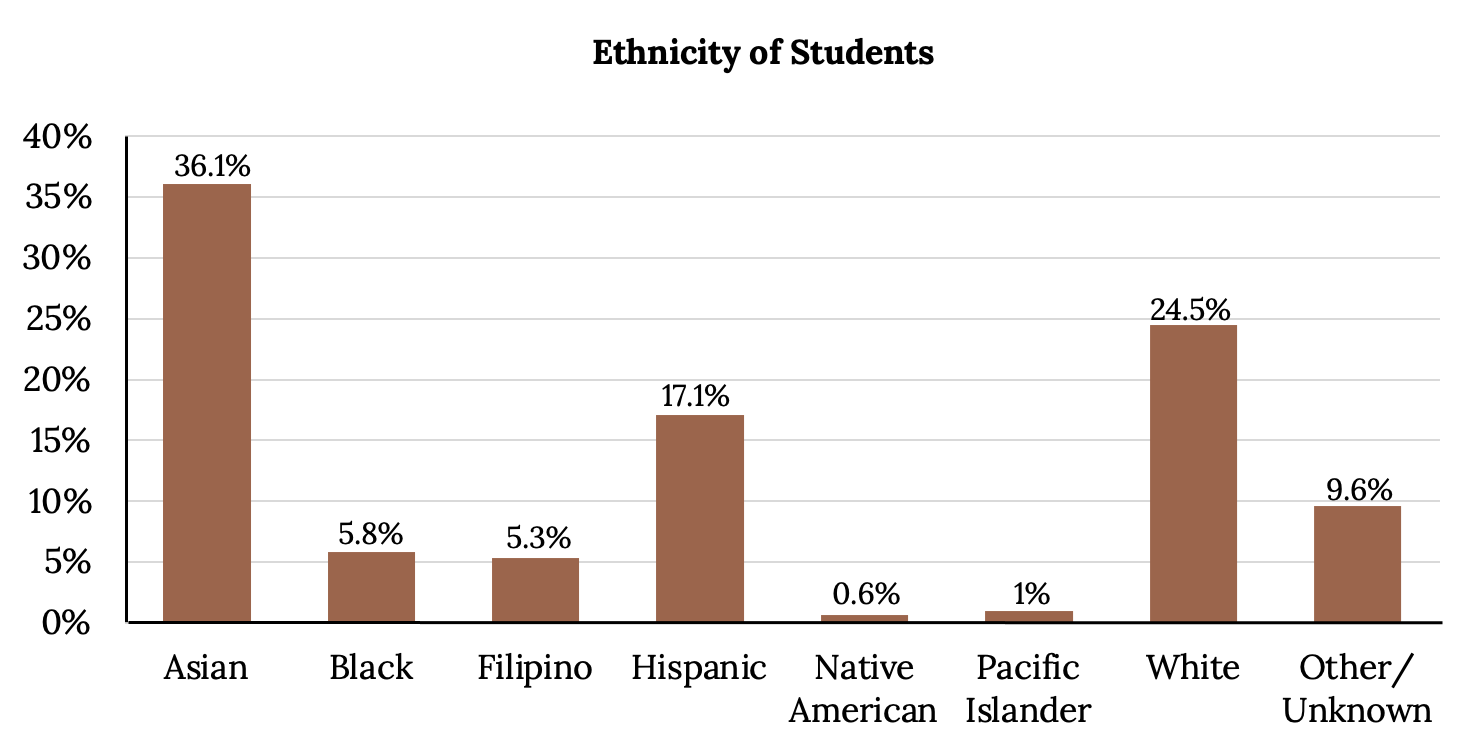
The following graph is the same as the previous graph but the “Other/Unknown” percent (9.6%) has been included. The “Other/Unknown” category is large compared to some of the other categories (Native American, 0.6%, Pacific Islander 1.0%). This is important to know when we think about what the data are telling us.
Bar Graph with Other/Unknown Category
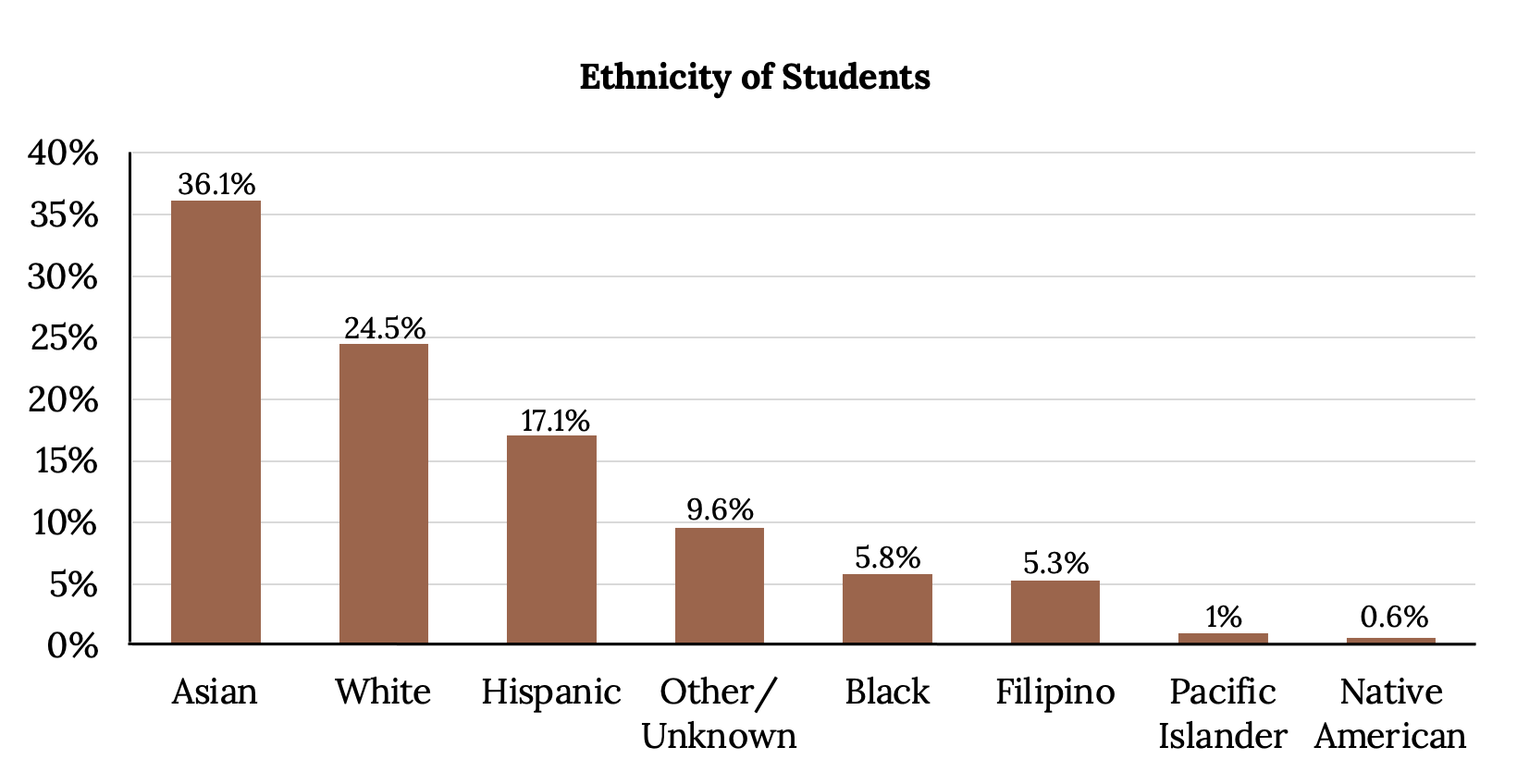
Pie Charts: No Missing Data
The following pie charts have the “Other/Unknown” category included (since the percentages must add to 100%). The second chart below is organized by the size of each wedge, which makes it a more visually informative graph than the unsorted, alphabetical graph in the first chart below.
Example
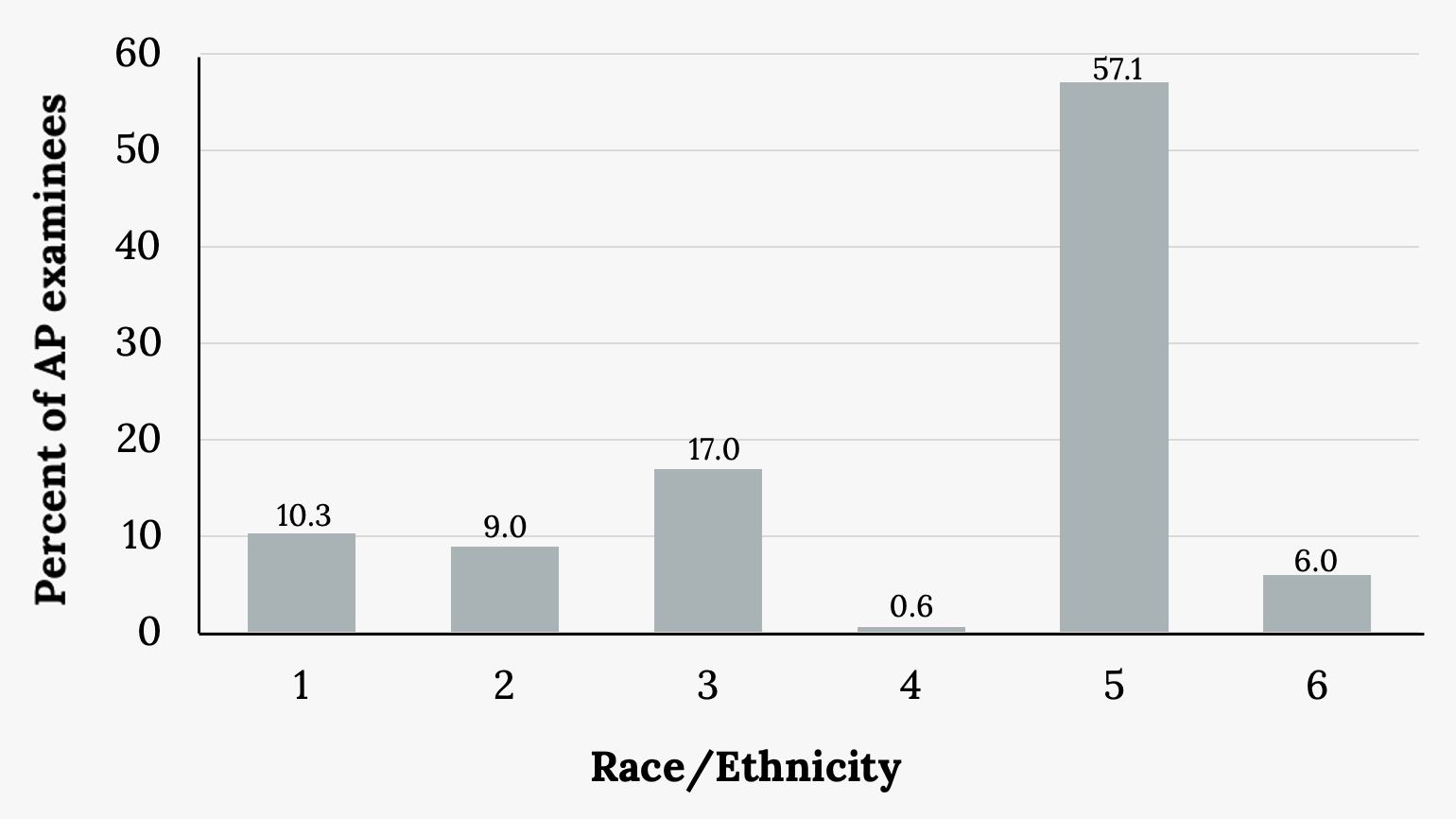
The columns in the figure below contain: the race or ethnicity of students in U.S. Public Schools for the class of 2011, percentages for the Advanced Placement examine population for that class, and percentages for the overall student population. Create a bar graph with the student race or ethnicity (qualitative data) on the x-axis, and the Advanced Placement examinee population percentages on the y-axis.
| Race/Ethnicity | AP Examinee Population | Overall Student Population |
|---|---|---|
| 1 = Asian, Asian American or Pacific Islander | 10.3% | 5.7% |
| 2 = Black or African American | 9.0% | 14.7% |
| 3 = Hispanic or Latino | 17.0% | 17.6% |
| 4 = American Indian or Alaska Native | 0.6% | 1.1% |
| 5 = White | 57.1% | 59.2% |
| 6 = Not reported/other | 6.0% | 1.7% |
Solution:
Your turn!
Park city is broken down into six voting districts. The table shows the percent of the total registered voter population that lives in each district as well as the percent total of the entire population that lives in each district. Construct a bar graph that shows the registered voter population by district.
| District | Registered voter population | Overall city population |
|---|---|---|
| 1 | 15.5% | 19.4% |
| 2 | 12.2% | 15.6% |
| 3 | 9.8% | 9.0% |
| 4 | 17.4% | 18.5% |
| 5 | 22.8% | 20.7% |
| 6 | 22.3% | 16.8% |
Construct a bar graph that shows the registered voter population by district.
Describing Categorical Data
After we have displayed the data visually, we then want to follow up by describing it with numerical measures. Since Categorical Data does not lend itself to mathematical calculations by nature there are not many numerical descriptors we can use to describe it. However, we can describe a categorical distribution’s “typical value” with the mode, and can also note its level of variability.
Mode
The Mode of a dataset is the most frequently occurring value. There can be more than one mode in a data set as long as those values have the same frequency and that frequency is the highest. A data set with two modes is called bimodal, three modes – trimodal, multiple modes – multimodal, etc. In most cases the mode can easily be found as the largest piece of a pie chart, or largest bar in a bar chart. Looking at some previous examples:


The mode of the class of Statistics students is obviously Freshman. If any doubt remains a Pareto chart makes identifying the mode trivial, which is Asian in the previous example.
Variability
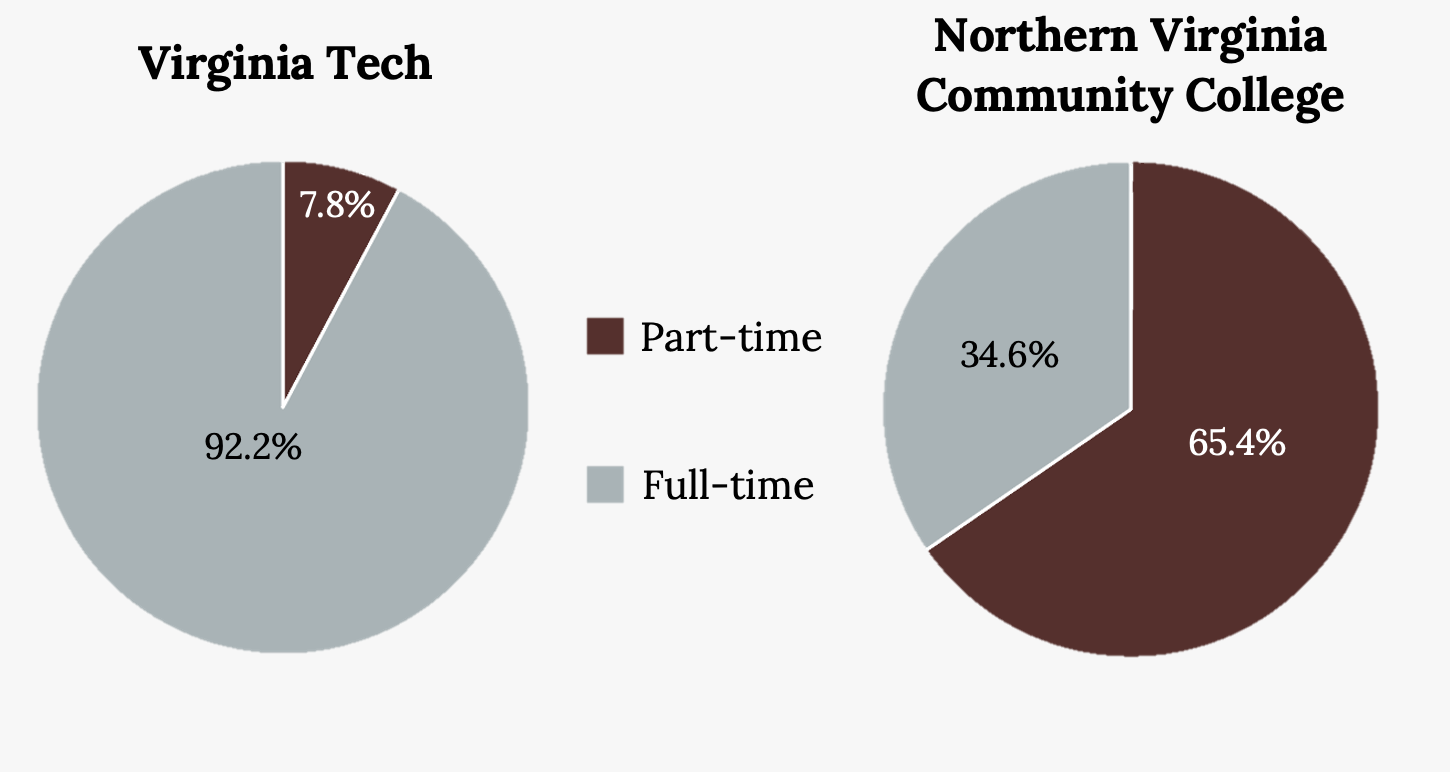
The best way to gauge variability in categorical data is by thinking about it as diversity. Although we will not calculate a numerical measure here, we can note it visually. A variable that has observations spread out fairly evenly over all categories shows high variability, while a variable where most observations are only in one or a handful of categories displays low variability. Consider the level of variability in the two pie charts below.
Example
Consider the level of variability in the two pie charts below. Which college has more variability?
Your turn!
Let’s consider the variability in the following bar charts. Which bar chart shows greater variability?
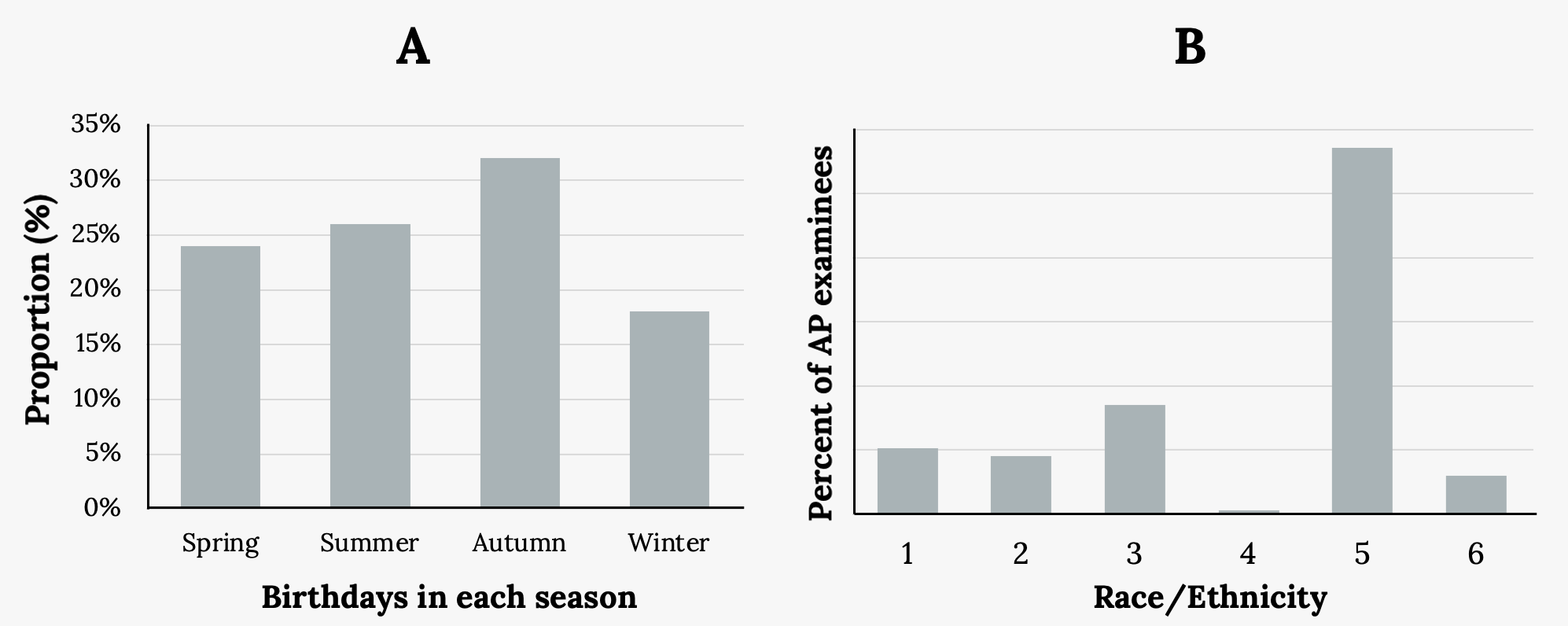
Image References
Figure 2.7: Kindred Grey (2020). “Classification of Statistics Students.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Classification_of_Statistics_Students.png
Figure 2.9: Kindred Grey (2020). “Ages and proportions.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Ages_and_proportions.png
Figure 2.10: Kindred Grey (2020). “Virginia Tech and NVCC stats.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Virginia_Tech_and_NVCC_stats.png
Figure 2.11: Kindred Grey (2020). “VT and NVCC chart.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:VT_and_NVCC_chart.png
Figure 2.13: Kindred Grey (2020). “Figure 2.13.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_2.13.png
Figure 2.15: Kindred Grey (2020). “Figure 2.15.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_2.15.png
Figure 2.16: Kindred Grey (2020). “Figure 2.16.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_2.16.png
Figure 2.17: Kindred Grey (2020). “Figure 2.17.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_2.17.png
Figure 2.18: Kindred Grey (2020). “Figure 2.18.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_2.18.png
Figure 2.20: Kindred Grey (2020). “Figure 2.20.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_2.20.png
Figure 2.22: Kindred Grey (2020). “Figure 2.22.” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_2.22.png
Data that describes qualities, or puts individuals into categories
The most frequently occurring value
The level of variability or dispersion of a dataset; also commonly known as variation/variability

