7.5 Behavior of Confidence Intervals for a Proportion

Confidence intervals for p behave similarly to intervals for μ, however there are a few subtleties.

Calculating the Sample Size n

If researchers desire a specific margin of error, then they can use the error bound formula to calculate the required sample size.

Recall the margin of error for a population proportion is:

  • MoE=\left({z}_{\frac{\alpha }{2}}\right)\left(\sqrt{\frac{\hat{p}\hat{q}}{n}}\right)
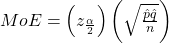
  • Solving for n gives you an equation for the sample size.
  • n=\left(\frac{{z}_{\frac{\alpha }{2}}}{MoE}\right)^{2}\text{p(1-p)}

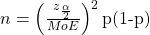
Recall the objective of a CI.  If we are looking to estimate p, then we do not know what is, however it appears in this formula.  So what do we plug in for p?  We have a few options:

  • If you have prior information such as a previous sample and can calculate a point estimate 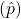\left(\hat{p}\right) plug it in!
  • You can use your best guess at p
  • You can use a “conservative” estimate of p, 0.5.*

*Note: Remember that \hat{q}=(1-\hat{p}). But, we do not know \hat{p} yet. Since we multiply \hat{p} and \hat{q} together, we make them both equal to 0.5 because \hat{p}\hat{q} = (0.5)(0.5) = 0.25 results in the largest possible product. (Try other products: (0.6)(0.4) = 0.24; (0.3)(0.7) = 0.21; (0.2)(0.8) = 0.16 and so on). The largest possible product gives us the largest n. This gives us a large enough sample so that we can be CL% confident that we are within three percentage points of the true population proportion.

Example

Suppose a mobile phone company wants to determine the current percentage of customers aged 50+ who use text messaging on their cell phones. How many customers aged 50+ should the company survey in order to be 90% confident that the estimated (sample) proportion is within three percentage points of the true population proportion of customers aged 50+ who use text messaging on their cell phones?

Your turn!

Suppose an internet marketing company wants to determine the current percentage of customers who click on ads on their smartphones. How many customers should the company survey in order to be 90% confident that the estimated proportion is within five percentage points of the true population proportion of customers who click on ads on their smartphones?

“Plus Four” Confidence Interval for p.   

This is an alternative optional method for constructing a CI for p, stemming from the continuity correction of the binomial approximation .

There is a certain amount of error introduced into the process of calculating a confidence interval for a proportion. Because we do not know the true proportion for the population, we are forced to use point estimates to calculate the appropriate standard deviation of the sampling distribution. Studies have shown that the resulting estimation of the standard deviation can be flawed.

Fortunately, there is a simple adjustment that allows us to produce more accurate confidence intervals. We simply pretend that we have four additional observations. Two of these observations are successes and two are failures. The new sample size, then, is n + 4, and the new count of successes is x + 2.

Computer studies have demonstrated the effectiveness of this method. It should be used when the confidence level desired is at least 90% and the sample size is at least ten.

Example

A random sample of 25 statistics students was asked: “Have you smoked a cigarette in the past week?” Six students reported smoking within the past week. Use the “plus-four” method to find a 95% confidence interval for the true proportion of statistics students who smoke.

Your turn!

Out of a random sample of 65 freshmen at State University, 31 students have declared a major. Use the “plus-four” method to find a 96% confidence interval for the true proportion of freshmen at State University who have declared a major.

definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Significant Statistics Copyright © 2020 by John Morgan Russell, OpenStaxCollege, OpenIntro is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book