7.2 Inference for the Mean in Practice
We have discussed the sampling distribution of the sample mean follows a normal distribution when the population standard deviation, σ, is known and the t distribution when it is not. In practice, we rarely know the population standard deviation. For larger samples we can typically get away with using Z according to the CLT. In summary, the majority of the time we opt to use t is when we do not know σ and we have a small sample (n<30)
Confidence Intervals for the Mean (σ Unknown)
The general format of a confidence interval is:
![]()
The population parameter is μ. The point estimate (PE) for μ is ![]() , the sample mean.
, the sample mean.
If the population standard deviation is not known, the margin of error (MoE) for a population mean is:
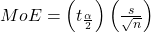 ,
,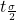 is the t critical value with area to the right equal to
is the t critical value with area to the right equal to 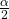 ,
,- use df = n – 1 degrees of freedom, and
- s = sample standard deviation.
Example
The Federal Election Commission (FEC) collects information about campaign contributions and disbursements for candidates and political committees each election cycle. A political action committee (PAC) is a committee formed to raise money for candidates and campaigns. A Leadership PAC is a PAC formed by a federal politician (senator or representative) to raise money to help other candidates’ campaigns.[1]
The FEC has reported financial information for 556 Leadership PACs that operated during the 2011–2012 election cycle. The following table shows the total receipts during this cycle for a random selection of 30 Leadership PACs. (In dollars)
| $46,500.00 | $0 | $40,966.50 | $105,887.20 | $5,175.00 |
| $29,050.00 | $19,500.00 | $181,557.20 | $31,500.00 | $149,970.80 |
| $2,555,363.20 | $12,025.00 | $409,000.00 | $60,521.70 | $18,000.00 |
| $61,810.20 | $76,530.80 | $119,459.20 | $0 | $63,520.00 |
| $6,500.00 | $502,578.00 | $705,061.10 | $708,258.90 | $135,810.00 |
| $2,000.00 | $2,000.00 | $0 | $1,287,933.80 | $219,148.30 |
![]() = $251,854.23
= $251,854.23
![]()
Use this sample data to construct a 96% confidence interval for the mean amount of money raised by all Leadership PACs during the 2011–2012 election cycle. Use the Student’s t-distribution.
Note that we are not given the population standard deviation, only the standard deviation of the sample.
Your turn!
A random sample of statistics students were asked to estimate the total number of hours they spend watching television in an average week. The responses are recorded in the figure below. Use this sample data to construct a 98% confidence interval for the mean number of hours statistics students will spend watching television in one week.
| 0 | 3 | 1 | 20 | 9 |
| 5 | 10 | 1 | 10 | 4 |
| 14 | 2 | 4 | 4 | 5 |
Hypothesis Tests for the Mean (σ Unknown)
Remember, we will use the t-distribution when the population standard deviation is unknown and the distribution of the sample mean is approximately normal.
If you are testing a single population mean, and we decide to use t, the steps say the same, but our test statistic will change slightly.
![]()
You should have no problem using technology to find p-values associated with a t test statistic. However, if you want to use your t table you’ll find it is somewhat limited in finding exact p-values. Despite that you can still estimate a range of values for your p-val and then compare it to your significance level.
Examples
Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores below:
65, 65, 70, 67, 66, 63, 63, 68, 72, 71
Perform the hypothesis test using a 5% level of significance to test the instructor’s claim.
Examples
It is believed that a stock price for a particular company will grow at a rate of $5 per week. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows:
$4, $3, $2, $3, $1, $7, $2, $1, $1, $2
Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p-value, state your conclusion, and identify the Type I and Type II errors.
Summary of Assumptions
When you perform inference on a single population mean μ using a Student’s t-distribution (often called a t-test), there are fundamental assumptions that need to be met in order for the test to work properly. Your data should be a simple random sample that comes from a population that is approximately normally distributed. You use the sample standard deviation to approximate the population standard deviation. (Note that if the sample size is sufficiently large, a t-test will work even if the population is not approximately normally distributed).
When you perform a hypothesis test of a single population mean μ using a normal distribution (often called a z-test), you take a simple random sample from the population. The population you are testing is normally distributed or your sample size is sufficiently large. You know the value of the population standard deviation which, in reality, is rarely known.
- “Disclosure Data Catalog: Candidate Summary Report 2012.” U.S. Federal Election Commission. Available online at http://www.fec.gov/data/index.jsp (accessed July 2, 2013). ↵
An interval built around a point estimate for an unknown population parameter
The value that is calculated from a sample used to estimate an unknown population parameter
How much a point estimate can be expected to differ from the true population value; made up of the standard error multiplied by the critical value
A family of t–distributions, dependent on degrees of freedom, similar to the normal distribution but with more variability built in

