Chapter 4 Wrap Up
Concept Check
Section Reviews
4.1 Introduction
The characteristics of a probability distribution function (PDF) for a discrete random variable are as follows:
- Each probability is between zero and one, inclusive (inclusive means to include zero and one).
- The sum of the probabilities is one.
4.2 Measures of General DRVs
The expected value, or mean, of a discrete random variable predicts the long-term results of a statistical experiment that has been repeated many times. The standard deviation of a probability distribution is used to measure the variability of possible outcomes.
Mean or Expected Value: ![]()
Standard Deviation: ![]()
4.3 The Binomial Distribution
A statistical experiment can be classified as a binomial experiment if the following conditions are met:
- There are a fixed number of trials, n.
- There are only two possible outcomes, called “success” and, “failure” for each trial. The letter p denotes the probability of a success on one trial and q denotes the probability of a failure on one trial.
- The n trials are independent and are repeated using identical conditions.
The outcomes of a binomial experiment fit a binomial probability distribution. The random variable X = the number of successes obtained in the n independent trials. The mean of X can be calculated using the formula μ = np, and the standard deviation is given by the formula σ = ![]() .
.
X ~ B(n, p) means that the discrete random variable X has a binomial probability distribution with n trials and probability of success p.
X = the number of successes in n independent trials
n = the number of independent trials
X takes on the values x = 0, 1, 2, 3, …, n
p = the probability of a success for any trial
q = the probability of a failure for any trial
p + q = 1
q = 1 – p
The mean of X is μ = np. The standard deviation of X is σ = ![]() .
.
Key Terms
Try to define the terms below on your own. Scroll over any term to check your response!
4.1 Introduction
- Random variable
- Probability model
- Discrete random variable
- Continuous random variable
- Probability mass function (PMF)
- Cumulative distribution function (CDF)
4.2 Measures of General DRVs
4.3 The Binomial Distribution
- Discrete random variable
- Binomial experiment
- Independent
- Bernoulli trial
- Probability mass function
- Cumulative distribution function
Extra Practice
4.1 Introduction
1. A company wants to evaluate its attrition rate, in other words, how long new hires stay with the company. Over the years, they have established the following probability distribution.Let X = the number of years a new hire will stay with the company. Let P(x) = the probability that a new hire will stay with the company x years. Complete the figure below using the data provided.
| x | P(x) |
|---|---|
| 0 | 0.12 |
| 1 | 0.18 |
| 2 | 0.30 |
| 3 | 0.15 |
| 4 | 0.10 |
| 5 | 0.10 |
| 6 | 0.05 |
a. P(x = 4) = _______
- 0.10
b. P(x ≥ 5) = _______
- 0.10 + 0.05 = 0.15
c. On average, how long would you expect a new hire to stay with the company?
- 0 + 0.18 + 0.60 + 0.45 + 0.40 + 0.50 + 0.30 = 2.43 years
d. What does the column “P(x)” sum to?
- 1
2. A baker is deciding how many batches of muffins to make to sell in his bakery. He wants to make enough to sell every one and no fewer. Through observation, the baker has established a probability distribution.
| x | P(x) |
|---|---|
| 1 | 0.15 |
| 2 | 0.35 |
| 3 | 0.40 |
| 4 | 0.10 |
a. Define the random variable X.
- Let X = the number of batches that the baker will sell.
b. What is the probability the baker will sell more than one batch? P(x > 1) = _______
- 0.35 + 0.40 + 0.10 = 0.85
c. What is the probability the baker will sell exactly one batch? P(x = 1) = _______
- 0.15
d. On average, how many batches should the baker make?
- 1(0.15) + 2(0.35) + 3(0.40) + 4(0.10) = 0.15 + 0.70 + 1.20 + 0.40 = 2.45
3. Ellen has music practice three days a week. She practices for all of the three days 85% of the time, two days 8% of the time, one day 4% of the time, and no days 3% of the time. One week is selected at random.
a. Define the random variable X.
- Let X = the number of days Ellen attends practice per week.
b. Construct a probability distribution table for the data.
| x | P(x) |
|---|---|
| 0 | 0.03 |
| 1 | 0.04 |
| 2 | 0.08 |
| 3 | 0.85 |
c. We know that for a probability distribution function to be discrete, it must have two characteristics. One is that the sum of the probabilities is one. What is the other characteristic?
- Each probability is between zero and one, inclusive.
4. Javier volunteers in community events each month. He does not do more than five events in a month. He attends exactly five events 35% of the time, four events 25% of the time, three events 20% of the time, two events 10% of the time, one event 5% of the time, and no events 5% of the time.
a. Define the random variable X.
- Let X = the number of events Javier volunteers for each month.
b. What values does x take on?
- 0, 1, 2, 3, 4, 5
c. Construct a PDF table.
| x | P(x) |
|---|---|
| 0 | 0.05 |
| 1 | 0.05 |
| 2 | 0.10 |
| 3 | 0.20 |
| 4 | 0.25 |
| 5 | 0.35 |
d. Find the probability that Javier volunteers for less than three events each month. P(x < 3) = _______
- 0.05 + 0.05 + 0.10 = 0.20
e. Find the probability that Javier volunteers for at least one event each month. P(x > 0) = _______
- 1 – 0.05 = 0.95
5. Suppose that the PDF for the number of years it takes to earn a Bachelor of Science (B.S.) degree is given in below.
| x | P(x) |
|---|---|
| 3 | 0.05 |
| 4 | 0.40 |
| 5 | 0.30 |
| 6 | 0.15 |
| 7 | 0.10 |
- In words, define the random variable X.
- What does it mean that the values zero, one, and two are not included for x in the PDF?
4.2 Measures of General DRVs
1. Suppose you play a game of chance in which five numbers are chosen from 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. A computer randomly selects five numbers from zero to nine with replacement. You pay $2 to play and could profit $100,000 if you match all five numbers in order (you get your $2 back plus $100,000). Over the long term, what is your expected profit of playing the game?
- To do this problem, set up an expected value table for the amount of money you can profit. Let X = the amount of money you profit. The values of x are not 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Since you are interested in your profit (or loss), the values of x are 100,000 dollars and −2 dollars.
- To win, you must get all five numbers correct, in order. The probability of choosing one correct number is
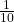 because there are ten numbers. You may choose a number more than once. The probability of choosing all five numbers correctly and in order is
because there are ten numbers. You may choose a number more than once. The probability of choosing all five numbers correctly and in order is 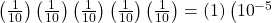 =0.00001.
=0.00001.- Therefore, the probability of winning is 0.00001 and the probability of losing is 1-0.00001=0.99999.
- The expected value table is as follows:
| x | P(x) | x*P(x) | |
|---|---|---|---|
| Loss | –2 | 0.99999 | (–2)(0.99999) = –1.99998 |
| Profit | 100,000 | 0.00001 | (100000)(0.00001) = 1 |
Since –0.99998 is about –1, you would, on average, expect to lose approximately $1 for each game you play. However, each time you play, you either lose $2 or profit $100,000. The $1 is the average or expected LOSS per game after playing this game over and over.
2. You are playing a game of chance in which four cards are drawn from a standard deck of 52 cards. You guess the suit of each card before it is drawn. The cards are replaced in the deck on each draw. You pay $1 to play. If you guess the right suit every time, you get your money back and $256. What is your expected profit of playing the game over the long term?
3. Suppose you play a game with a biased coin. You play each game by tossing the coin once. P(heads) = ![]() and P(tails) =
and P(tails) = ![]() . If you toss a head, you pay $6. If you toss a tail, you win $10. If you play this game many times, will you come out ahead?
. If you toss a head, you pay $6. If you toss a tail, you win $10. If you play this game many times, will you come out ahead?
a. Define a random variable X.
- X = amount of profit
b. Complete the following expected value table.
| x | ____ | ____ | |
|---|---|---|---|
| WIN | 10 | ____ | |
| LOSE | ____ | ____ |
| x | P(x) | xP(x) | |
|---|---|---|---|
| WIN | 10 | ||
| LOSE | –6 |
c. What is the expected value, μ? Do you come out ahead?
- Add the last column of the table. The expected value μ =
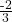 . You lose, on average, about 67 cents each time you play the game so you do not come out ahead.
. You lose, on average, about 67 cents each time you play the game so you do not come out ahead.
4. Suppose you play a game with a spinner. You play each game by spinning the spinner once. P(red) = ![]() , P(blue) =
, P(blue) = ![]() , and P(green) =
, and P(green) = ![]() . If you land on red, you pay $10. If you land on blue, you don’t pay or win anything. If you land on green, you win $10. Complete the following expected value table.
. If you land on red, you pay $10. If you land on blue, you don’t pay or win anything. If you land on green, you win $10. Complete the following expected value table.
| x | P(x) | ||
|---|---|---|---|
| Red | – |
||
| Blue | |||
| Green | 10 |
5. Toss a fair, six-sided die twice. Let X = the number of faces that show an even number. Construct a table like the one in Number 4 and calculate the mean μ and standard deviation σ of X.
Tossing one fair six-sided die twice has the same sample space as tossing two fair six-sided dice. The sample space has 36 outcomes:
| (1, 1) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) |
| (2, 1) | (2, 2) | (2, 3) | (2, 4) | (2, 5) | (2, 6) |
| (3, 1) | (3, 2) | (3, 3) | (3, 4) | (3, 5) | (3, 6) |
| (4, 1) | (4, 2) | (4, 3) | (4, 4) | (4, 5) | (4, 6) |
| (5, 1) | (5, 2) | (5, 3) | (5, 4) | (5, 5) | (5, 6) |
| (6, 1) | (6, 2) | (6, 3) | (6, 4) | (6, 5) | (6, 6) |
Use the sample space to complete the following table:
| x | P(x) | xP(x) | (x – μ)2 ⋅ P(x) |
|---|---|---|---|
| 0 | 0 | (0 – 1)2 ⋅ |
|
| 1 | (1 – 1)2 ⋅ |
||
| 2 | (1 – 1)2 ⋅ |
Add the values in the third column to find the expected value: μ = ![]() = 1. Use this value to complete the fourth column.
= 1. Use this value to complete the fourth column.
Add the values in the fourth column and take the square root of the sum: σ = ![]()
6. On May 11, 2013 at 9:30 PM, the probability that moderate seismic activity (one moderate earthquake) would occur in the next 48 hours in Iran was about 21.42%. Suppose you make a bet that a moderate earthquake will occur in Iran during this period. If you win the bet, you win $50. If you lose the bet, you pay $20. Let X = the amount of profit from a bet. [1]
P(win) = P(one moderate earthquake will occur) = 21.42%
P(loss) = P(one moderate earthquake will not occur) = 100% – 21.42%
If you bet many times, will you come out ahead? Explain your answer in a complete sentence using numbers. What is the standard deviation of X? Construct a table similar to the ones in 4 and 5 to help you answer these questions.
| x | P(x) | x(Px) | (x – μ)2P(x) | |
|---|---|---|---|---|
| win | 50 | 0.2142 | 10.71 | [50 – (–5.006)]2(0.2142) = 648.0964 |
| loss | –20 | 0.7858 | –15.716 | [–20 – (–5.006)]2(0.7858) = 176.6636 |
Mean = Expected Value = 10.71 + (–15.716) = –5.006.
If you make this bet many times under the same conditions, your long term outcome will be an average loss of $5.01 per bet.
![]()
7. Complete the expected value table.
| x | P(x) | x*P(x) |
|---|---|---|
| 0 | 0.2 | |
| 1 | 0.2 | |
| 2 | 0.4 | |
| 3 | 0.2 |
8. Find the expected value from the expected value table.
| x | P(x) | x*P(x) |
|---|---|---|
| 2 | 0.1 | 2(0.1) = 0.2 |
| 4 | 0.3 | 4(0.3) = 1.2 |
| 6 | 0.4 | 6(0.4) = 2.4 |
| 8 | 0.2 | 8(0.2) = 1.6 |
- 0.2 + 1.2 + 2.4 + 1.6 = 5.4
Find the standard deviation.
| x | P(x) | x*P(x) | (x – μ)2P(x) |
|---|---|---|---|
| 2 | 0.1 | 2(0.1) = 0.2 | (2–5.4)2(0.1) = 1.156 |
| 4 | 0.3 | 4(0.3) = 1.2 | (4–5.4)2(0.3) = 0.588 |
| 6 | 0.4 | 6(0.4) = 2.4 | (6–5.4)2(0.4) = 0.144 |
| 8 | 0.2 | 8(0.2) = 1.6 | (8–5.4)2(0.2) = 1.352 |
- σ= 1.156+0.588+0.144+1.352 = 3.24 =1.8
9. Identify the mistake in the probability distribution table.
| x | P(x) | x*P(x) |
|---|---|---|
| 1 | 0.15 | 0.15 |
| 2 | 0.25 | 0.50 |
| 3 | 0.30 | 0.90 |
| 4 | 0.20 | 0.80 |
| 5 | 0.15 | 0.75 |
- The values of P(x) do not sum to one.
10. Identify the mistake in the probability distribution table.
| x | P(x) | x*P(x) |
|---|---|---|
| 1 | 0.15 | 0.15 |
| 2 | 0.25 | 0.40 |
| 3 | 0.25 | 0.65 |
| 4 | 0.20 | 0.85 |
| 5 | 0.15 | 1 |
- The values of xP(x) are not correct.
11. A physics professor wants to know what percent of physics majors will spend the next several years doing post-graduate research. He has the following probability distribution.
| x | P(x) | x*P(x) |
|---|---|---|
| 1 | 0.35 | |
| 2 | 0.20 | |
| 3 | 0.15 | |
| 4 | ||
| 5 | 0.10 | |
| 6 | 0.05 |
a. Define the random variable X.
- Let X = the number of years a physics major will spend doing post-graduate research.
b. Define P(x), or the probability of x.
- Let P(x) = the probability that a physics major will do post-graduate research for x years.
c. Find the probability that a physics major will do post-graduate research for four years. P(x = 4) = _______
- 1 – 0.35 – 0.20 – 0.15 – 0.10 – 0.05 = 0.15
d. Find the probability that a physics major will do post-graduate research for at most three years. P(x ≤ 3) = _______
- 0.35 + 0.20 + 0.15 = 0.70
e. On average, how many years would you expect a physics major to spend doing post-graduate research?
- 1(0.35) + 2(0.20) + 3(0.15) + 4(0.15) + 5(0.10) + 6(0.05) = 0.35 + 0.40 + 0.45 + 0.60 + 0.50 + 0.30 = 2.6 years
12. A ballet instructor is interested in knowing what percent of each year’s class will continue on to the next, so that she can plan what classes to offer. Over the years, she has established the following probability distribution.
- Let X = the number of years a student will study ballet with the teacher.
- Let P(x) = the probability that a student will study ballet x years.
Complete the figure below using the data provided.
| x | P(x) | x*P(x) |
|---|---|---|
| 1 | 0.10 | |
| 2 | 0.05 | |
| 3 | 0.10 | |
| 4 | ||
| 5 | 0.30 | |
| 6 | 0.20 | |
| 7 | 0.10 |
a. In words, define the random variable X.
- X is the number of years a student studies ballet with the teacher.
b. P(x = 4) = _______
- 1 – 0.10 – 0.05 – 0.10 – 0.30 – 0.20 – 0.10 = 0.15
c. P(x < 4) = _______
- 0.10 + 0.05 + 0.10 = 0.25
d. On average, how many years would you expect a child to study ballet with this teacher?
- 1(0.10) + 2(0.05) + 3(0.10) + 4(0.15) + 5(0.30) + 6(0.20) + 7(0.10) = 4.5 years
e. What does the column “P(x)” sum to and why?
- The sum of the probabilities sum to one because it is a probability distribution.
f. What does the column “x*P(x)” sum to and why?
- The sum of xP(x) = 4.5; it is the mean of the distribution.
13. You are playing a game by drawing a card from a standard deck and replacing it. If the card is a face card, you win $30. If it is not a face card, you pay $2. There are 12 face cards in a deck of 52 cards.
a. What is the expected value of playing the game?
![]() =-1.54+6.92=5.38
=-1.54+6.92=5.38
b. Should you play the game?
Yes, because there is a positive expected value, and the more you play, the more likely you are to get closer to the expected value.
14. A theater group holds a fund-raiser. It sells 100 raffle tickets for $5 apiece. Suppose you purchase four tickets. The prize is two passes to a Broadway show, worth a total of $150.
- What are you interested in here?
- In words, define the random variable X.
- List the values that X may take on.
- Construct a PDF.
- If this fund-raiser is repeated often and you always purchase four tickets, what would be your expected average winnings per raffle?
- I am interested in the average profit or loss. Let X = the return from the raffle Win($150) or Lose ($0)
- 150( 1 100 )+0( 99 100 )−20=−$18.50
15. A game involves selecting a card from a regular 52-card deck and tossing a coin. The coin is a fair coin and is equally likely to land on heads or tails.
- If the card is a face card, and the coin lands on Heads, you win $6
- If the card is a face card, and the coin lands on Tails, you win $2
- If the card is not a face card, you lose $2, no matter what the coin shows.
- Find the expected value for this game (expected net gain or loss).
- Explain what your calculations indicate about your long-term average profits and losses on this game.
- Should you play this game to win money?
The variable of interest is X, or the gain or loss, in dollars.
The face cards jack, queen, and king. There are (3)(4) = 12 face cards and 52 – 12 = 40 cards that are not face cards.
We first need to construct the probability distribution for X. We use the card and coin events to determine the probability for each outcome, but we use the monetary value of X to determine the expected value.
| Card Event | X net gain/loss | P(X) |
|---|---|---|
| Face Card and Heads | 6 | |
| Face Card and Tails | 2 | |
| (Not Face Card) and (H or T) | –2 |
- Expected value=
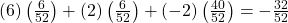 = –$0.62 (rounded to the nearest cent)
= –$0.62 (rounded to the nearest cent) - If you play this game repeatedly, over a long string of games, you would expect to lose 62 cents per game, on average.
- You should not play this game to win money because the expected value indicates an expected average loss.
16. You buy a lottery ticket to a lottery that costs $10 per ticket. There are only 100 tickets available to be sold in this lottery. In this lottery there are one $500 prize, two $100 prizes, and four $25 prizes. Find your expected gain or loss.
- Start by writing the probability distribution. X is net gain or loss = prize (if any) less $10 cost of ticket.
- Expected Value =(490)( 1 100 )+(90)( 2 100 )+(15)( 4 100 )+(−10)( 93 100 )=−$2. There is an expected loss of $2 per ticket, on average.
Complete the PDF and answer the questions.
| x | P(x) | xP(x) |
|---|---|---|
| 0 | 0.3 | |
| 1 | 0.2 | |
| 2 | ||
| 3 | 0.4 |
- Find the probability that x = 2.
- Find the expected value.
- 0.1
- 1.6
17. Suppose that you are offered the following “deal.” You roll a die. If you roll a six, you win $10. If you roll a four or five, you win $5. If you roll a one, two, or three, you pay $6.
- What are you ultimately interested in here (the value of the roll or the money you win)?
- In words, define the Random Variable X.
- List the values that X may take on.
- Construct a PDF.
- Over the long run of playing this game, what are your expected average winnings per game?
- Based on numerical values, should you take the deal? Explain your decision in complete sentences.
- the money won X = the amount of money won or lost $5, –$6, $10
- Expected Value = (10) 1 6 + (5) 2 6 – (6) 3 6 = 0.33 Yes, the expected value is 33 cents
18. A venture capitalist, willing to invest $1,000,000, has three investments to choose from. The first investment, a software company, has a 10% chance of returning $5,000,000 profit, a 30% chance of returning $1,000,000 profit, and a 60% chance of losing the million dollars. The second company, a hardware company, has a 20% chance of returning $3,000,000 profit, a 40% chance of returning $1,000,000 profit, and a 40% chance of losing the million dollars. The third company, a biotech firm, has a 10% chance of returning $6,000,000 profit, a 70% of no profit or loss, and a 20% chance of losing the million dollars.
- Construct a PDF for each investment.
- Find the expected value for each investment.
- Which is the safest investment? Why do you think so?
- Which is the riskiest investment? Why do you think so?
- Which investment has the highest expected return, on average?
-
Figure 4.29: Software Company x P(x) 5,000,000 0.10 1,000,000 0.30 –1,000,000 0.60 Figure 4.30: Hardware Company x P(x) 3,000,000 0.20 1,000,000 0.40 –1,000,00 0.40 Figure 4.31: Biotech Firm x P(x) 6,00,000 0.10 0 0.70 –1,000,000 0.20 - $200,000; $600,000; $400,000
- third investment because it has the lowest probability of loss
- first investment because it has the highest probability of loss
- second investment
19. Suppose that 20,000 married adults in the United States were randomly surveyed as to the number of children they have. The results are compiled and are used as theoretical probabilities. Let X = the number of children married people have.
| x | P(x) | xP(x) |
|---|---|---|
| 0 | 0.10 | |
| 1 | 0.20 | |
| 2 | 0.30 | |
| 3 | ||
| 4 | 0.10 | |
| 5 | 0.05 | |
| 6 (or more) | 0.05 |
- Find the probability that a married adult has three children.
- In words, what does the expected value in this example represent?
- Find the expected value.
- Is it more likely that a married adult will have two to three children or four to six children? How do you know?
- 0.2
- The average number of children married adults have 2.35
- two to three children
20. Suppose that the PDF for the number of years it takes to earn a Bachelor of Science (B.S.) degree is given below.
| x | P(x) |
|---|---|
| 3 | 0.05 |
| 4 | 0.40 |
| 5 | 0.30 |
| 6 | 0.15 |
| 7 | 0.10 |
a. On average, how many years do you expect it to take for an individual to earn a B.S.?
- 4.85 years
21. People visiting video rental stores often rent more than one DVD at a time. The probability distribution for DVD rentals per customer at Video To Go is given in the following table. There is a five-video limit per customer at this store, so nobody ever rents more than five DVDs.
| x | P(x) |
|---|---|
| 0 | 0.03 |
| 1 | 0.50 |
| 2 | 0.24 |
| 3 | |
| 4 | 0.07 |
| 5 | 0.04 |
- Describe the random variable X in words.
- Find the probability that a customer rents three DVDs.
- Find the probability that a customer rents at least four DVDs.
- Find the probability that a customer rents at most two DVDs.
Another shop, Entertainment Headquarters, rents DVDs and video games. The probability distribution for DVD rentals per customer at this shop is given as follows. They also have a five-DVD limit per customer.
| x | P(x) |
|---|---|
| 0 | 0.35 |
| 1 | 0.25 |
| 2 | 0.20 |
| 3 | 0.10 |
| 4 | 0.05 |
| 5 | 0.05 |
- At which store is the expected number of DVDs rented per customer higher?
- If Video to Go estimates that they will have 300 customers next week, how many DVDs do they expect to rent next week? Answer in sentence form.
- If Video to Go expects 300 customers next week, and Entertainment HQ projects that they will have 420 customers, for which store is the expected number of DVD rentals for next week higher? Explain.
- Which of the two video stores experiences more variation in the number of DVD rentals per customer? How do you know that?
Solutions:
X = the number of video rentals per costumer 0.12 0.11 0.77 Video To Go (1.82 expected value vs. 1.4 for Entertainment Headquarters) The expected number of videos rented to 300 Video To Go customers is 546. The expected number of videos rented to 420 Entertainment Headquarters customers is 588. Entertainment Headquarters will rent more videos. The standard deviation for the number of videos rented at Video To Go is 1.1609. The standard deviation for the number of videos rented at Entertainment Headquarters is 1.4293. Entertainment Headquarters has more variation.
22. A “friend” offers you the following “deal.” For a $10 fee, you may pick an envelope from a box containing 100 seemingly identical envelopes. However, each envelope contains a coupon for a free gift.
- Ten of the coupons are for a free gift worth $6.
- Eighty of the coupons are for a free gift worth $8.
- Six of the coupons are for a free gift worth $12.
- Four of the coupons are for a free gift worth $40.
Based upon the financial gain or loss over the long run, should you play the game?
- Yes, I expect to come out ahead in money.
- No, I expect to come out behind in money.
- It doesn’t matter. I expect to break even.
- Answer: b
23. Florida State University has 14 statistics classes scheduled for its Summer 2013 term. One class has space available for 30 students, eight classes have space for 60 students, one class has space for 70 students, and four classes have space for 100 students. [2]
- What is the average class size assuming each class is filled to capacity?
- Space is available for 980 students. Suppose that each class is filled to capacity and select a statistics student at random. Let the random variable X equal the size of the student’s class. Define the PDF for X.
- Find the mean of X.
- Find the standard deviation of X.
- Solutions: The average class size is: 30+8(60)+70+4(100) 14 =70 P(x=30)= 1 14 P(x=60)= 8 14 P(x=70)= 1 14 P(x=100)= 4 14 Complete the following table to find the mean and standard deviation of X. Mean of X= 30 14 + 480 14 + 70 14 + 400 14 = 980 14 =70 Standard Deviation of X= 114.2857+57.1429+0+257.1429 =20.702
24. In a lottery, there are 250 prizes of $5, 50 prizes of $25, and ten prizes of $100. Assuming that 10,000 tickets are to be issued and sold, what is a fair price to charge to break even?
Let X = the amount of money to be won on a ticket. The following table shows the PDF for X.
| x | P(x) |
|---|---|
| 0 | 0.969 |
| 5 | |
| 25 | |
| 100 |
a. Calculate the expected value of X.
- 0(0.969) + 5(0.025) + 25(0.005) + 100(0.001) = 0.35
- A fair price for a ticket is $0.35. Any price over $0.35 will enable the lottery to raise money.
4.3 The Binomial Distribution
1. The state health board is concerned about the amount of fruit available in school lunches. Forty-eight percent of schools in the state offer fruit in their lunches every day. This implies that 52% do not. What would a “success” be in this case?
2. A trainer is teaching a dolphin to do tricks. The probability that the dolphin successfully performs the trick is 35%, and the probability that the dolphin does not successfully perform the trick is 65%. Out of 20 attempts, you want to find the probability that the dolphin succeeds 12 times. State the probability question mathematically.
3. A fair, six-sided die is rolled ten times. Each roll is independent. You want to find the probability of rolling a one more than three times. State the probability question mathematically.
4. The lifetime risk of developing pancreatic cancer is about one in 78 (1.28%). [3] Suppose we randomly sample 200 people. Let X = the number of people who will develop pancreatic cancer.
- What is the probability distribution for X?
- Using the formulas, calculate the (i) mean and (ii) standard deviation of X.
- Find the probability that at most eight people develop pancreatic cancer
- Is it more likely that five or six people will develop pancreatic cancer? Justify your answer numerically.
5. During the 2013 regular NBA season, DeAndre Jordan of the Los Angeles Clippers had the highest field goal completion rate in the league. DeAndre scored with 61.3% of his shots.[4] Suppose you choose a random sample of 80 shots made by DeAndre during the 2013 season. Let X = the number of shots that scored points.
- What is the probability distribution for X?
- Using the formulas, calculate the (i) mean and (ii) standard deviation of X.
- Find the probability that DeAndre scored with 60 of these shots.
- Find the probability that DeAndre scored with more than 50 of these shots.
6. A lacrosse team is selecting a captain. The names of all the seniors are put into a hat, and the first three that are drawn will be the captains. The names are not replaced once they are drawn (one person cannot be two captains). You want to see if the captains all play the same position. State whether this is binomial or not and state why.
7. The Higher Education Research Institute at UCLA collected data from 203,967 incoming first-time, full-time freshmen from 270 four-year colleges and universities in the U.S. 71.3% of those students replied that, yes, they believe that same-sex couples should have the right to legal marital status.[5] Suppose that you randomly pick eight first-time, full-time freshmen from the survey. You are interested in the number that believes that same sex-couples should have the right to legal marital status.
a. In words, define the random variable X.
- X = the number that reply “yes”
b. X ~ _____(_____,_____)
- B(8,0.713)
c. What values does the random variable X take on?
- 0, 1, 2, 3, 4, 5, 6, 7, 8
d. Construct the probability distribution function (PDF).
| x | P(x) |
|---|---|
e. On average (μ), how many would you expect to answer yes?
- 5.7
f. What is the standard deviation (σ)?
- 1.2795
g. What is the probability that at most five of the freshmen reply “yes”?
- 0.4151
h. What is the probability that at least two of the freshmen reply “yes”?
- 0.9990
8. According to a recent article the average number of babies born with significant hearing loss (deafness) is approximately two per 1,000 babies in a healthy baby nursery. The number climbs to an average of 30 per 1,000 babies in an intensive care nursery. Suppose that 1,000 babies from healthy baby nurseries were randomly surveyed. Find the probability that exactly two babies were born deaf.
- 0.2709
9. Use the following information to answer the next four exercises. Recently, a nurse commented that when a patient calls the medical advice line claiming to have the flu, the chance that he or she truly has the flu (and not just a nasty cold) is only about 4%. Of the next 25 patients calling in claiming to have the flu, we are interested in how many actually have the flu.
a. Define the random variable and list its possible values.
- X = the number of patients calling in claiming to have the flu, who actually have the flu.
- X = 0, 1, 2, …25
b. State the distribution of X.
- B(25,0.04)
c. Find the probability that at least four of the 25 patients actually have the flu.
- 0.0165
d. On average, for every 25 patients calling in, how many do you expect to have the flu?
- one
10. People visiting video rental stores often rent more than one DVD at a time. The probability distribution for DVD rentals per customer at Video To Go is given below. There is five-video limit per customer at this store, so nobody ever rents more than five DVDs.
| x | P(x) |
|---|---|
| 0 | 0.03 |
| 1 | 0.50 |
| 2 | 0.24 |
| 3 | |
| 4 | 0.07 |
| 5 | 0.04 |
- Describe the random variable X in words.
- Find the probability that a customer rents three DVDs.
- Find the probability that a customer rents at least four DVDs.
- Find the probability that a customer rents at most two DVDs.
- X = the number of DVDs a Video to Go customer rents
- 0.12
- 0.11
- 0.77
11. A school newspaper reporter decides to randomly survey 12 students to see if they will attend Tet (Vietnamese New Year) festivities this year. Based on past years, she knows that 18% of students attend Tet festivities. We are interested in the number of students who will attend the festivities.
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- How many of the 12 students do we expect to attend the festivities?
- Find the probability that at most four students will attend.
- Find the probability that more than two students will attend.
Solutions: X = the number of students who will attend Tet. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 X ~ B(12,0.18) 2.16 0.9511 0.3702
12. The probability that the San Jose Sharks will win any given game is 0.3694 based on a 13-year win history of 382 wins out of 1,034 games played (as of a certain date). [6]An upcoming monthly schedule contains 12 games.
a. The expected number of wins for that upcoming month is:
- 1.67
- 12
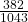
- 4.43
- d
b. Let X = the number of games won in that upcoming month. What is the probability that the San Jose Sharks win six games in that upcoming month?
- 0.1476
- 0.2336
- 0.7664
- 0.8903
- a
c. What is the probability that the San Jose Sharks win at least five games in that upcoming month
- 0.3694
- 0.5266
- 0.4734
- 0.2305
- c
13. A student takes a ten-question true-false quiz, but did not study and randomly guesses each answer. Find the probability that the student passes the quiz with a grade of at least 70% of the questions correct.
Solution: X = number of questions answered correctly X ~ B(10, 0.5) We are interested in AT LEAST 70% of ten questions correct. 70% of ten is seven. We want to find the probability that X is greater than or equal to seven. The event “at least seven” is the complement of “less than or equal to six”. Use your software or calculator to get 0.171875. The probability of getting at least 70% of the ten questions correct when randomly guessing is approximately 0.172.
14. A student takes a 32-question multiple-choice exam, but did not study and randomly guesses each answer. Each question has three possible choices for the answer. Find the probability that the student guesses more than 75% of the questions correctly.
- X = number of questions answered correctly
- X ~ B
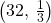
- We are interested in MORE THAN 75% of 32 questions correct. 75% of 32 is 24. We want to find P(x > 24). The event “more than 24” is the complement of “less than or equal to 24.”
- Using your technology of choice: 1 – binomcdf(32,1/3,24)
- P(x > 24) = 0
- The probability of getting more than 75% of the 32 questions correct when randomly guessing is very small and practically zero.
15. Six different colored dice are rolled. Of interest is the number of dice that show a one.
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- On average, how many dice would you expect to show a one?
- Find the probability that all six dice show a one.
- Is it more likely that three or that four dice will show a one? Use numbers to justify your answer numerically.
Solution: X = the number of dice that show a one 0, 1, 2, 3, 4, 5, 6 X ~ B ( 6, 1 6 ) 1 0.00002 three dice
16. More than 96 percent of the very largest colleges and universities (more than 15,000 total enrollments) have some online offerings. Suppose you randomly pick 13 such institutions. We are interested in the number that offer distance learning courses.
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- On average, how many schools would you expect to offer such courses?
- Find the probability that at most ten offer such courses.
- Is it more likely that 12 or that 13 will offer such courses? Use numbers to justify your answer numerically and answer in a complete sentence.
- X = the number of college and universities that offer online offerings.
- 0, 1, 2, …, 13
- X ~ B(13, 0.96)
- 12.48
- 0.0135
- P(x = 12) = 0.3186 P(x = 13) = 0.5882 More likely to get 13.
17. Suppose that about 85% of graduating students attend their graduation. A group of 22 graduating students is randomly chosen.
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- How many are expected to attend their graduation?
- Find the probability that 17 or 18 attend.
- Based on numerical values, would you be surprised if all 22 attended graduation? Justify your answer numerically.
Solution: X = the number of students who attend their graduation 0, 1, 2, …, 22 X ~ B(22, 0.85) 18.7 0.3249 P(x = 22) = 0.0280 (less than 3%) which is unusual
18. At The Fencing Center, 60% of the fencers use the foil as their main weapon. We randomly survey 25 fencers at The Fencing Center. We are interested in the number of fencers who do not use the foil as their main weapon.
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- How many are expected to not to use the foil as their main weapon?
- Find the probability that six do not use the foil as their main weapon.
- Based on numerical values, would you be surprised if all 25 did not use foil as their main weapon? Justify your answer numerically.
- X = the number of fencers who do not use the foil as their main weapon
- 0, 1, 2, 3,… 25
- X ~ B(25,0.40)
- 10
- 0.0442
- The probability that all 25 not use the foil is almost zero. Therefore, it would be very surprising.
19. Approximately 8% of students at a local high school participate in after-school sports all four years of high school. A group of 60 seniors is randomly chosen. Of interest is the number who participated in after-school sports all four years of high school.
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- How many seniors are expected to have participated in after-school sports all four years of high school?
- Based on numerical values, would you be surprised if none of the seniors participated in after-school sports all four years of high school? Justify your answer numerically.
- Based upon numerical values, is it more likely that four or that five of the seniors participated in after-school sports all four years of high school? Justify your answer numerically.
Solution: X = the number of high school students who participate in after school sports all four years of high school. 0, 1, 2, …, 60 X ~ B(60, 0.08) 4.8 Yes, P(x = 0) = 0.0067, which is a small probability P(x = 4) = 0.1873, P(x = 5) = 0.1824. More likely to get four.
20. The chance of an IRS audit for a tax return with over $25,000 in income is about 2% per year. We are interested in the expected number of audits a person with that income has in a 20-year period. Assume each year is independent.
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- How many audits are expected in a 20-year period?
- Find the probability that a person is not audited at all.
- Find the probability that a person is audited more than twice.
- X = the number of audits in a 20-year period
- 0, 1, 2, …, 20
- X ~ B(20, 0.02)
- 0.4
- 0.6676
- 0.0071
21. It has been estimated that only about 30% of California residents have adequate earthquake supplies. Suppose you randomly survey 11 California residents. We are interested in the number who have adequate earthquake supplies.[7]
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- What is the probability that at least eight have adequate earthquake supplies?
- Is it more likely that none or that all of the residents surveyed will have adequate earthquake supplies? Why?
- How many residents do you expect will have adequate earthquake supplies?
Solution: X = the number of California residents who do have adequate earthquake supplies. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 B(11, 0.30) 0.0043 P(x = 0) = 0.0198. P(x = 11) = 0 or none 3.3
22. There are two similar games played for Chinese New Year and Vietnamese New Year. In the Chinese version, fair dice with numbers 1, 2, 3, 4, 5, and 6 are used, along with a board with those numbers. In the Vietnamese version, fair dice with pictures of a gourd, fish, rooster, crab, crayfish, and deer are used. The board has those six objects on it, also. We will play with bets being $1. The player places a bet on a number or object. The “house” rolls three dice. If none of the dice show the number or object that was bet, the house keeps the $1 bet. If one of the dice shows the number or object bet (and the other two do not show it), the player gets back his or her $1 bet, plus $1 profit. If two of the dice show the number or object bet (and the third die does not show it), the player gets back his or her $1 bet, plus $2 profit. If all three dice show the number or object bet, the player gets back his or her $1 bet, plus $3 profit. Let X = number of matches and Y = profit per game.
- In words, define the random variable X.
- List the values that X may take on.
- Give the distribution of X. X ~ _____(_____,_____)
- List the values that Y may take on. Then, construct one PDF table that includes both X and Y and their probabilities.
- Calculate the average expected matches over the long run of playing this game for the player.
- Calculate the average expected earnings over the long run of playing this game for the player.
- Determine who has the advantage, the player or the house.
- X = the number of matches
- 0, 1, 2, 3
- X ~ B(3,
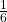 )
) - In dollars: −1, 1, 2, 3
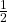
- Multiply each Y value by the corresponding X probability from the PDF table. The answer is −0.0787. You lose about eight cents, on average, per game.
- The house has the advantage.
23. According to The World Bank, only 9% of the population of Uganda had access to electricity as of 2009. Suppose we randomly sample 150 people in Uganda. Let X = the number of people who have access to electricity.
- What is the probability distribution for X?
- Using the formulas, calculate the mean and standard deviation of X.
- Find the probability that 15 people in the sample have access to electricity.
- Find the probability that at most ten people in the sample have access to electricity.
- Find the probability that more than 25 people in the sample have access to electricity.
Solution: X ~ B(150,0.09) Mean = np = 150(0.09) = 13.5 Standard Deviation = npq = 150(0.09)(0.91) ≈ 3.5050 P(x = 15) = binompdf(150, 0.09, 15) = 0.0988 P(x ≤ 10) = binomcdf(150, 0.09, 10) = 0.1987 P(x > 25) = 1 – P(x ≤ 25) = 1 – binomcdf(150, 0.09, 25) = 1 – 0.9991 = 0.0009
24. The literacy rate for a nation measures the proportion of people age 15 and over that can read and write. The literacy rate in Afghanistan is 28.1%. Suppose you choose 15 people in Afghanistan at random. Let X = the number of people who are literate. [8]
- Sketch a graph of the probability distribution of X.
- Using the formulas, calculate the (i) mean and (ii) standard deviation of X.
- Find the probability that more than five people in the sample are literate. Is it is more likely that three people or four people are literate.
- X ~ B(15, 0.281)
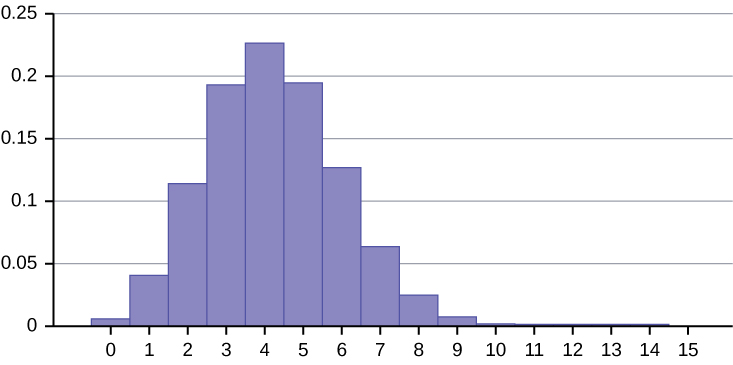
Figure 4.39 - Mean = μ = np = 15(0.281) = 4.215
- Standard Deviation = σ =
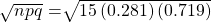 = 1.7409
= 1.7409
- P(x > 5) = 1 – P(x ≤ 5) = 1 – binomcdf(15, 0.281, 5) = 1 – 0.7754 = 0.2246
P(x = 3) = binompdf(15, 0.281, 3) = 0.1927
P(x = 4) = binompdf(15, 0.281, 4) = 0.2259
It is more likely that four people are literate that three people are.
References
Image References
Figure 4.39: Figure 4.10 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/4-solutions#fs-idm104093808-solution
Text
Class Catalogue at the Florida State University. Available online at https://apps.oti.fsu.edu/RegistrarCourseLookup/SearchFormLegacy (accessed May 15, 2013).
“World Earthquakes: Live Earthquake News and Highlights,” World Earthquakes, 2012. http://www.world-earthquakes.com/index.php?option=ethq_prediction (accessed May 15, 2013).
“Access to electricity (% of population),” The World Bank, 2013. Available online at http://data.worldbank.org/indicator/EG.ELC.ACCS.ZS?order=wbapi_data_value_2009%20wbapi_data_value%20wbapi_data_value-first&sort=asc (accessed May 15, 2015).
“Distance Education.” Wikipedia. Available online at http://en.wikipedia.org/wiki/Distance_education (accessed May 15, 2013).
“NBA Statistics – 2013,” ESPN NBA, 2013. Available online at http://espn.go.com/nba/statistics/_/seasontype/2 (accessed May 15, 2013).
Newport, Frank. “Americans Still Enjoy Saving Rather than Spending: Few demographic differences seen in these views other than by income,” GALLUP® Economy, 2013. Available online at http://www.gallup.com/poll/162368/americans-enjoy-saving-rather-spending.aspx (accessed May 15, 2013).
Pryor, John H., Linda DeAngelo, Laura Palucki Blake, Sylvia Hurtado, Serge Tran. The American Freshman: National Norms Fall 2011. Los Angeles: Cooperative Institutional Research Program at the Higher Education Research Institute at UCLA, 2011. Also available online at http://heri.ucla.edu/PDFs/pubs/TFS/Norms/Monographs/TheAmericanFreshman2011.pdf (accessed May 15, 2013).
“The World FactBook,” Central Intelligence Agency. Available online at https://www.cia.gov/library/publications/the-world-factbook/geos/af.html (accessed May 15, 2013).
“What are the key statistics about pancreatic cancer?” American Cancer Society, 2013. Available online at http://www.cancer.org/cancer/pancreaticcancer/detailedguide/pancreatic-cancer-key-statistics (accessed May 15, 2013).
- “World Earthquakes: Live Earthquake News and Highlights,” World Earthquakes, 2012. http://www.worldearthquakes.com/index.php?option=ethq_prediction (accessed May 15, 2013). ↵
- Class Catalogue at the Florida State University. Available online at https://apps.oti.fsu.edu/RegistrarCourseLookup/ SearchFormLegacy (accessed May 15, 2013). ↵
- “What are the key statistics about pancreatic cancer?” American Cancer Society, 2013. Available online at http://www.cancer.org/cancer/pancreaticcancer/detailedguide/pancreatic-cancer-key-statistics (accessed May 15, 2013). ↵
- “NBA Statistics – 2013,” ESPN NBA, 2013. Available online at http://espn.go.com/nba/statistics/_/seasontype/2 (accessed May 15, 2013). ↵
- Pryor, John H., Linda DeAngelo, Laura Palucki Blake, Sylvia Hurtado, Serge Tran. The American Freshman: National Norms Fall 2011. Los Angeles: Cooperative Institutional Research Program at the Higher Education Research Institute at UCLA, 2011. Also available online at http://heri.ucla.edu/PDFs/pubs/TFS/Norms/Monographs/ TheAmericanFreshman2011.pdf (accessed May 15, 2013). ↵
- Hockey Reference - San Jose Sharks https://www.hockey-reference.com/teams/SJS/history.html (accessed January 26, 2021). ↵
- “World Earthquakes: Live Earthquake News and Highlights,” World Earthquakes, 2012. http://www.worldearthquakes.com/index.php?option=ethq_prediction (accessed May 15, 2013). ↵
- “UNICEF reports on Female Literacy Centers in Afghanistan established to teach women and girls basic resading [sic] 300 Chapter 4 | Discrete Random Variables This OpenStax book is available for free at http://cnx.org/content/col11562/1.18 and writing skills,” UNICEF Television. Video available online at http://www.unicefusa.org/assets/video/afghan-femaleliteracy-centers.html (accessed May 15, 2013). ↵
A representation of a probability model
A mathematical representation of a random process that lists all possible outcomes and assigns probabilities to each of them
A random variable that produces discrete data
A random variable (RV) whose outcomes are measured as an uncountable, infinite, number of values
A function that gives the probability that a discrete random variable is exactly equal to some value (x)
A function that gives the probability that a random variable takes a value less than or equal to x
Mean of a random variable
A random variable that counts the number of successes in a fixed number (n) of independent Bernoulli trials each with probability of a success (p)
The occurrence of one event has no effect on the probability of the occurrence of another event
An experiment with the following characteristics:
- There are only two possible outcomes called “success” and “failure” for each trial
- The probability (p) of a success is the same for any trial (so the probability q = 1 − p of a failure is the same for any trial)

