Group and Partner Projects
Univariate Data
Student Learning Objectives
- The student will design and carry out a survey.
- The student will analyze and graphically display the results of the survey.
Instructions
As you complete each task below, check it off. Answer all questions in your summary.
____ Decide what data you are going to study.
Here are two examples, but you may NOT use them: number of M&M’s per bag, number of pencils students have in their backpacks.
____ Are your data discrete or continuous? How do you know?
____ Decide how you are going to collect the data (for instance, buy 30 bags of M&M’s; collect data from the World Wide Web).
____ Describe your sampling technique in detail. Use cluster, stratified, systematic, or simple random (using a random number generator) sampling. Do not use convenience sampling. Which method did you use? Why did you pick that method?
____ Conduct your survey. Your data size must be at least 30.
____ Summarize your data in a chart with columns showing data value, frequency, relative frequency and cumulative relative frequency.
Answer the following (rounded to two decimal places):
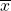 = _____
= _____- s = _____
- First quartile = _____
- Median = _____
- 70th percentile = _____
____ What value is two standard deviations above the mean?
____ What value is 1.5 standard deviations below the mean?
____ Construct a histogram displaying your data.
____ In complete sentences, describe the shape of your graph.
____ Do you notice any potential outliers? If so, what values are they? Show your work in how you used the potential outlier formula to determine whether or not the values might be outliers.
____ Construct a box plot displaying your data.
____ Does the middle 50% of the data appear to be concentrated together or spread apart? Explain how you determined this.
____ Looking at both the histogram and the box plot, discuss the distribution of your data.
Assignment Checklist
You need to turn in the following typed and stapled packet, with pages in the following order:
- Cover sheet: name, class time, and name of your study
- Summary page: This should contain paragraphs written with complete sentences. It should include answers to all the questions above. It should also include statements describing the population under study, the sample, a parameter or parameters being studied, and the statistic or statistics produced.
- URL for data, if your data are from the World Wide Web
- Chart of data, frequency, relative frequency, and cumulative relative frequency
- Page(s) of graphs: histogram and box plot
Continuous Distributions and Central Limit Theorem
Student Learning Objectives
- The student will collect a sample of continuous data.
- The student will attempt to fit the data sample to various distribution models.
- The student will validate the central limit theorem.
Instructions
As you complete each task below, check it off. Answer all questions in your summary.
Part I: Sampling
____ Decide what continuous data you are going to study. (Here are two examples, but you may NOT use them: the amount of money a student spent on college supplies this term, or the length of time distance telephone call lasts.)
____ Describe your sampling technique in detail. Use cluster, stratified, systematic, or simple random (using a random number generator) sampling. Do not use convenience sampling. What method did you use? Why did you pick that method?
____ Conduct your survey. Gather at least 150 pieces of continuous, quantitative data.
____ Define (in words) the random variable for your data. X = _______
____ Create two lists of your data: (1) unordered data, (2) in order of smallest to largest.
____ Find the sample mean and the sample standard deviation (rounded to two decimal places).
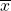 = ______
= ______- s = ______
____ Construct a histogram of your data containing five to ten intervals of equal width. The histogram should be a representative display of your data. Label and scale it.
Part II: Possible Distributions
____ Suppose that X followed the following theoretical distributions. Set up each distribution using the appropriate information from your data.
____ Uniform: X ~ U ____________ Use the lowest and highest values as a and b.
____ Normal: X ~ N ____________ Use ![]() to estimate for μ and s to estimate for σ.
to estimate for μ and s to estimate for σ.
____ Must your data fit one of the above distributions? Explain why or why not.
____ Could the data fit two or three of the previous distributions (at the same time)? Explain.
____ Calculate the value k(an X value) that is 1.75 standard deviations above the sample mean. k = _________ (rounded to two decimal places) Note: k = ![]() + (1.75)s
+ (1.75)s
____ Determine the relative frequencies (RF) rounded to four decimal places.
![]()
- RF(X < k) = ______
- RF(X > k) = ______
- RF(X = k) = ______
You should have one page for the uniform distribution, one page for the exponential distribution, and one page for the normal distribution.
____ State the distribution: X ~ _________
____ Draw a graph for each of the three theoretical distributions. Label the axes and mark them appropriately.
____ Find the following theoretical probabilities (rounded to four decimal places).
- P(X < k) = ______
- P(X > k) = ______
- P(X = k) = ______
____ Compare the relative frequencies to the corresponding probabilities. Are the values close?
____ Does it appear that the data fit the distribution well? Justify your answer by comparing the probabilities to the relative frequencies, and the histograms to the theoretical graphs.
Part III: CLT Experiments
______ From your original data (before ordering), use a random number generator to pick 40 samples of size five. For each sample, calculate the average.
______ On a separate page, attached to the summary, include the 40 samples of size five, along with the 40 sample averages.
______ List the 40 averages in order from smallest to largest.
______ Define the random variable, ![]() , in words.
, in words. ![]() = _______________
= _______________
______ State the approximate theoretical distribution of ![]() .
. ![]() ~ ______________
~ ______________
______ Base this on the mean and standard deviation from your original data.
______ Construct a histogram displaying your data. Use five to six intervals of equal width. Label and scale it.
Calculate the value ![]() (an
(an ![]() value) that is 1.75 standard deviations above the sample mean.
value) that is 1.75 standard deviations above the sample mean. ![]() = _____ (rounded to two decimal places)
= _____ (rounded to two decimal places)
Determine the relative frequencies (RF) rounded to four decimal places.
- RF(
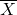 <
< 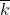 ) = _______
) = _______ - RF(
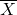 >
> 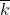 ) = _______
) = _______ - RF(
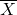 =
= 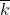 ) = _______
) = _______
Find the following theoretical probabilities (rounded to four decimal places).
- P(
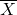 <
< 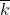 ) = _______
) = _______ - P(
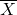 >
> 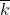 ) = _______
) = _______ - P(
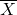 =
= 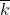 ) = _______
) = _______
______ Draw the graph of the theoretical distribution of ![]() .
.
______ Compare the relative frequencies to the probabilities. Are the values close?
______ Does it appear that the data of averages fit the distribution of ![]() well? Justify your answer by comparing the probabilities to the relative frequencies, and the histogram to the theoretical graph.
well? Justify your answer by comparing the probabilities to the relative frequencies, and the histogram to the theoretical graph.
In three to five complete sentences for each, answer the following questions. Give thoughtful explanations.
______ In summary, do your original data seem to fit the uniform, exponential, or normal distributions? Answer why or why not for each distribution. If the data do not fit any of those distributions, explain why.
______ What happened to the shape and distribution when you averaged your data? In theory, what should have happened? In theory, would “it” always happen? Why or why not?
______ Were the relative frequencies compared to the theoretical probabilities closer when comparing the ![]() or
or ![]() distributions? Explain your answer.
distributions? Explain your answer.
Assignment Checklist
You need to turn in the following typed and stapled packet, with pages in the following order:
____ Cover sheet: name, class time, and name of your study
____ Summary pages: These should contain several paragraphs written with complete sentences that describe the experiment, including what you studied and your sampling technique, as well as answers to all of the questions previously asked questions
____ URL for data, if your data are from the World Wide Web
____ Pages, one for each theoretical distribution, with the distribution stated, the graph, and the probability questions answered
____ Pages of the data requested
____ All graphs required
Hypothesis Testing-Article
Student Learning Objectives
- The student will identify a hypothesis testing problem in print.
- The student will conduct a survey to verify or dispute the results of the hypothesis test.
- The student will summarize the article, analysis, and conclusions in a report.
Instructions
As you complete each task, check it off. Answer all questions in your summary.
____Find an article in a newspaper, magazine, or on the internet which makes a claim about ONE population mean or ONE population proportion. The claim may be based upon a survey that the article was reporting on. Decide whether this claim is the null or alternate hypothesis.
____Copy or print out the article and include a copy in your project, along with the source.
____State how you will collect your data. (Convenience sampling is not acceptable.)
____Conduct your survey. You must have more than 50 responses in your sample. When you hand in your final project, attach the tally sheet or the packet of questionnaires that you used to collect data. Your data must be real.
____State the statistics that are a result of your data collection: sample size, sample mean, and sample standard deviation, OR sample size and number of successes.
____Make two copies of the appropriate solution sheet.
____Record the hypothesis test on the solution sheet, based on your experiment. Do a DRAFT solution first on one of the solution sheets and check it over carefully. Have a classmate check your solution to see if it is done correctly. Make your decision using a 5% level of significance. Include the 95% confidence interval on the solution sheet.
____Create a graph that illustrates your data. This may be a pie or bar graph or may be a histogram or box plot, depending on the nature of your data. Produce a graph that makes sense for your data and gives useful visual information about your data. You may need to look at several types of graphs before you decide which is the most appropriate for the type of data in your project.
____Write your summary (in complete sentences and paragraphs, with proper grammar and correct spelling) that describes the project. The summary MUST include:
- Brief discussion of the article, including the source
- Statement of the claim made in the article (one of the hypotheses).
- Detailed description of how, where, and when you collected the data, including the sampling technique; did you use cluster, stratified, systematic, or simple random sampling (using a random number generator)? As previously mentioned, convenience sampling is not acceptable.
- Conclusion about the article claim in light of your hypothesis test; this is the conclusion of your hypothesis test, stated in words, in the context of the situation in your project in sentence form, as if you were writing this conclusion for a non-statistician.
- Sentence interpreting your confidence interval in the context of the situation in your project
Assignment Checklist
Turn in the following typed (12 point) and stapled packet for your final project:
____Cover sheet containing your name(s), class time, and the name of your study
____Summary, which includes all items listed on summary checklist
____Solution sheet neatly and completely filled out. The solution sheet does not need to be typed.
____Graphic representation of your data, created following the guidelines previously discussed; include only graphs which are appropriate and useful.
____Raw data collected AND a table summarizing the sample data (n, ![]() and s; or x, n, and p’, as appropriate for your hypotheses); the raw data does not need to be typed, but the summary does. Hand in the data as you collected it. (Either attach your tally sheet or an envelope containing your questionnaires.)
and s; or x, n, and p’, as appropriate for your hypotheses); the raw data does not need to be typed, but the summary does. Hand in the data as you collected it. (Either attach your tally sheet or an envelope containing your questionnaires.)
Bivariate Data, Linear Regression, and Univariate Data
Student Learning Objectives
- The students will collect a bivariate data sample through the use of appropriate sampling techniques.
- The student will attempt to fit the data to a linear model.
- The student will determine the appropriateness of linear fit of the model.
- The student will analyze and graph univariate data.
Instructions
- As you complete each task below, check it off. Answer all questions in your introduction or summary.
- Check your course calendar for intermediate and final due dates.
- Graphs may be constructed by hand or by computer, unless your instructor informs you otherwise. All graphs must be neat and accurate.
- All other responses must be done on the computer.
- Neatness and quality of explanations are used to determine your final grade.
Part I: Bivariate Data
Introduction____State the bivariate data your group is going to study.
Here are two examples, but you may NOT use them: height vs. weight and age vs. running distance.
____Describe your sampling technique in detail. Use cluster, stratified, systematic, or simple random sampling (using a random number generator) sampling. Convenience sampling is NOT acceptable.
____Conduct your survey. Your number of pairs must be at least 30.
____Print out a copy of your data.
Analysis ____On a separate sheet of paper construct a scatter plot of the data. Label and scale both axes.
____State the least squares line and the correlation coefficient.
____On your scatter plot, in a different color, construct the least squares line.
____Is the correlation coefficient significant? Explain and show how you determined this.
____Interpret the slope of the linear regression line in the context of the data in your project. Relate the explanation to your data, and quantify what the slope tells you.
____Does the regression line seem to fit the data? Why or why not? If the data does not seem to be linear, explain if any other model seems to fit the data better.
____Are there any outliers? If so, what are they? Show your work in how you used the potential outlier formula in the Linear Regression and Correlation chapter (since you have bivariate data) to determine whether or not any pairs might be outliers.
Part II: Univariate Data
In this section, you will use the data for ONE variable only. Pick the variable that is more interesting to analyze. For example: if your independent variable is sequential data such as year with 30 years and one piece of data per year, your x-values might be 1971, 1972, 1973, 1974, …, 2000. This would not be interesting to analyze. In that case, choose to use the dependent variable to analyze for this part of the project.
_____Summarize your data in a chart with columns showing data value, frequency, relative frequency, and cumulative relative frequency.
_____Answer the following question, rounded to two decimal places:
- Sample mean = ______
- Sample standard deviation = ______
- First quartile = ______
- Third quartile = ______
- Median = ______
- 70th percentile = ______
- Value that is 2 standard deviations above the mean = ______
- Value that is 1.5 standard deviations below the mean = ______
_____Construct a histogram displaying your data. Group your data into six to ten intervals of equal width. Pick regularly spaced intervals that make sense in relation to your data. For example, do NOT group data by age as 20-26,27-33,34-40,41-47,48-54,55-61 . . . Instead, maybe use age groups 19.5-24.5, 24.5-29.5, . . . or 19.5-29.5, 29.5-39.5, 39.5-49.5, . . .
_____In complete sentences, describe the shape of your histogram.
_____Are there any potential outliers? Which values are they? Show your work and calculations as to how you used the potential outlier formula in Descriptive Statistics (since you are now using univariate data) to determine which values might be outliers.
_____Construct a box plot of your data.
_____Does the middle 50% of your data appear to be concentrated together or spread out? Explain how you determined this.
_____Looking at both the histogram AND the box plot, discuss the distribution of your data. For example: how does the spread of the middle 50% of your data compare to the spread of the rest of the data represented in the box plot; how does this correspond to your description of the shape of the histogram; how does the graphical display show any outliers you may have found; does the histogram show any gaps in the data that are not visible in the box plot; are there any interesting features of your data that you should point out.
Due Dates
- Part I, Intro: __________ (keep a copy for your records)
- Part I, Analysis: __________ (keep a copy for your records)
-
Entire Project, typed and stapled: __________
____ Cover sheet: names, class time, and name of your study
____ Part I: label the sections “Intro” and “Analysis.”
____ Part II:
____ Summary page containing several paragraphs written in complete sentences describing the experiment, including what you studied and how you collected your data. The summary page should also include answers to ALL the questions asked above.
____ All graphs requested in the project
____ All calculations requested to support questions in data
____ Description: what you learned by doing this project, what challenges you had, how you overcame the challenges
Include answers to ALL questions asked, even if not explicitly repeated in the items above.

