8.1 Inference for Two Dependent Samples (Matched Pairs)

Learning Objectives

By the end of this chapter, the student should be able to:

  • Classify hypothesis tests by type
  • Conduct and interpret hypothesis tests for two population means, population standard deviations known
  • Conduct and interpret hypothesis tests for two population means, population standard deviations unknown
  • Conduct and interpret hypothesis tests for matched or paired samples
  • Conduct and interpret hypothesis tests for two population proportions

 

Ariel picture of a table full of breakfast food including waffles, fruit, breads, coffee, etc.
Figure 8.1: Types of Breakfasts. If you want to test a claim that involves two groups (the types of breakfasts eaten east and west of the Mississippi River) we will use a two sample analysis.

Studies often compare two groups. For example, maybe researchers are interested in the effect aspirin has in preventing heart attacks.  One group is given aspirin and the other a placebo, and the heart attack rate is studied over several years.  Other studies may compare various diet and exercise programs.  Politicians compare the proportion of individuals from different income brackets who might vote for them. Students are interested in whether SAT or GRE preparatory courses really help raise their scores.

You have learned to conduct inference on single means and single proportions.  We know that the first step is deciding what type of data we are working with.  For quantitative data we are focused on means, while for categorical we are focused on proportions.  In this chapter we will compare two means or two proportions to each other.  The general procedure is still the same, just expanded.  With two sample analysis it is good to know what the formulas look like and where they come from, however you will probably lean heavily on technology in preforming the calculations.  

To compare two means we are obviously working with two groups, but first we need to think about the relationship between them. The groups are classified either as independent or dependent.  Independent samples consist of two samples that have no relationship, that is, sample values selected from one population are not related in any way to sample values selected from the other population.  Dependent samples consist of two groups that have some sort of identifiable relationship.

Two Dependent Samples (Matched Pairs)

Two samples that are dependent typically come from a matched pairs experimental design. The parameter tested using matched pairs is the population mean difference.  When using inference techniques for matched or paired samples, the following characteristics should be present:

  1. Simple random sampling is used.
  2. Sample sizes are often small.
  3. Two measurements (samples) are drawn from the same pair of (or two extremely similar) individuals or objects.
  4. Differences are calculated from the matched or paired samples.
  5. The differences form the sample that is used for analysis.

To perform statistical inference techniques we first need to know about the sampling distribution of our parameter of interest. Remember although we start with two samples, the differences are the data we are interested in and our parameter of interest is μd, the mean difference.  Our point estimate is \overline{x}_d.  In a perfect world we could assume that both samples come from a normal distribution, therefore the difference in those normal distributions are also normal.  However in order to use Z, we must know the population standard deviation which is near impossible for a difference distribution.  Also it is very hard to find large numbers of matched pairs so the sampling distribution we typically use for \overline{x}_d is a t distribution with n – 1 degrees of freedom, where n is the number of differences.

Confidence intervals may be calculated on their own for two samples but often, especially in the case of matched pairs, we first want to formally check to see if a difference exists with a hypothesis test.  If we do find a statistically significant difference then we may estimate it with a CI after the fact.

Hypothesis Tests for the Mean difference

In a hypothesis test for matched or paired samples, subjects are matched in pairs and differences are calculated, and the population mean difference, μd, is our parameter of interest.  Although it is possible to test for a certain magnitude of effect, we are most often just looking for a general effect.  Our hypothesis would then look like:

Ho: μd=0

Ha: μd(<, >, ≠) 0

The steps are the same as we are familiar with, but it is tested using a Student’s-t test for a single population mean with n – 1 degrees of freedom, with the test statistic:

t=\(\frac{{\overline{x}}_{d}-{\mu }_{d}}{\left(\frac{{s}_{d}}{\sqrt{n}}\right)}

Example

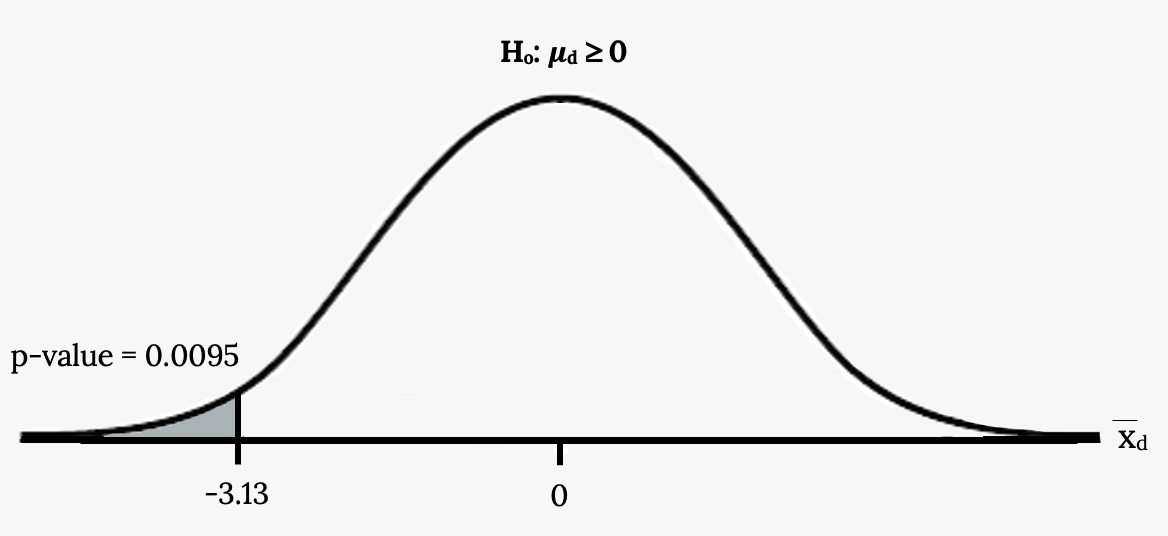
A study was conducted to investigate the effectiveness of hypnotism in reducing pain. Results for randomly selected subjects are shown in the figure below. A lower score indicates less pain. The “before” value is matched to an “after” value and the differences are calculated. The differences have a normal distribution. Are the sensory measurements, on average, lower after hypnotism? Test at a 5% significance level.

Figure 8.2: Reported Pain Data
Subject: A B C D E F G H
Before 6.6 6.5 9.0 10.3 11.3 8.1 6.3 11.6
After 6.8 2.4 7.4 8.5 8.1 6.1 3.4 2.0

 

Normal distribution curve showing the values 0 and -3.13. -3.13 is associated with p-value 0.0095 and everything to the left of this is shaded.
Figure 8.3: Reported Pain P-Value

Your turn!

A study was conducted to investigate how effective a new diet was in lowering cholesterol. Results for the randomly selected subjects are shown in the table. The differences have a normal distribution. Are the subjects’ cholesterol levels lower on average after the diet? Test at the 5% level.

Figure 8.4: Cholesterol Levels
Subject A B C D E F G H I
Before 209 210 205 198 216 217 238 240 222
After 199 207 189 209 217 202 211 223 201

Confidence Intervals for the Mean difference

The general format of a confidence interval is:
(PE-MoE, PE+MoE)

The population parameter of interest is μd, the mean difference.  Our point estimate is \overline{x}_d

If we are using the t distribution, the error bound for the population mean difference is:

  • MoE=\left({t}_{\frac{\alpha }{2}}\right)\left(\frac{s_d}{\sqrt{n}}\right),
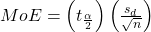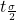  • {t}_{\frac{\sigma }{2}} is the t critical value with area to the right equal to \frac{\alpha }{2},
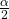  • use df = n – 1 degrees of freedom, where n is the number of pairs
  • sd =  standard deviation of the differences.

Example

A college football coach was interested in whether the college’s strength development class increased his players’ maximum lift (in pounds) on the bench press exercise. He asked four of his players to participate in a study. The amount of weight they could each lift was recorded before they took the strength development class. After completing the class, the amount of weight they could each lift was again measured. The data are as follows:

Figure 8.5: Weight Lifted
Weight (in pounds) Player 1 Player 2 Player 3 Player 4
Amount of weight lifted prior to the class 205 241 338 368
Amount of weight lifted after the class 295 252 330 360

The coach wants to know if the strength development class makes his players stronger, on average.

Using the differences data, calculate the sample mean and the sample standard deviation.

Using the difference data, this becomes a test of a single __________ (fill in the blank).

Define the random variable:{\overline{X}}_{d} mean difference in the maximum lift per player.

Graph:

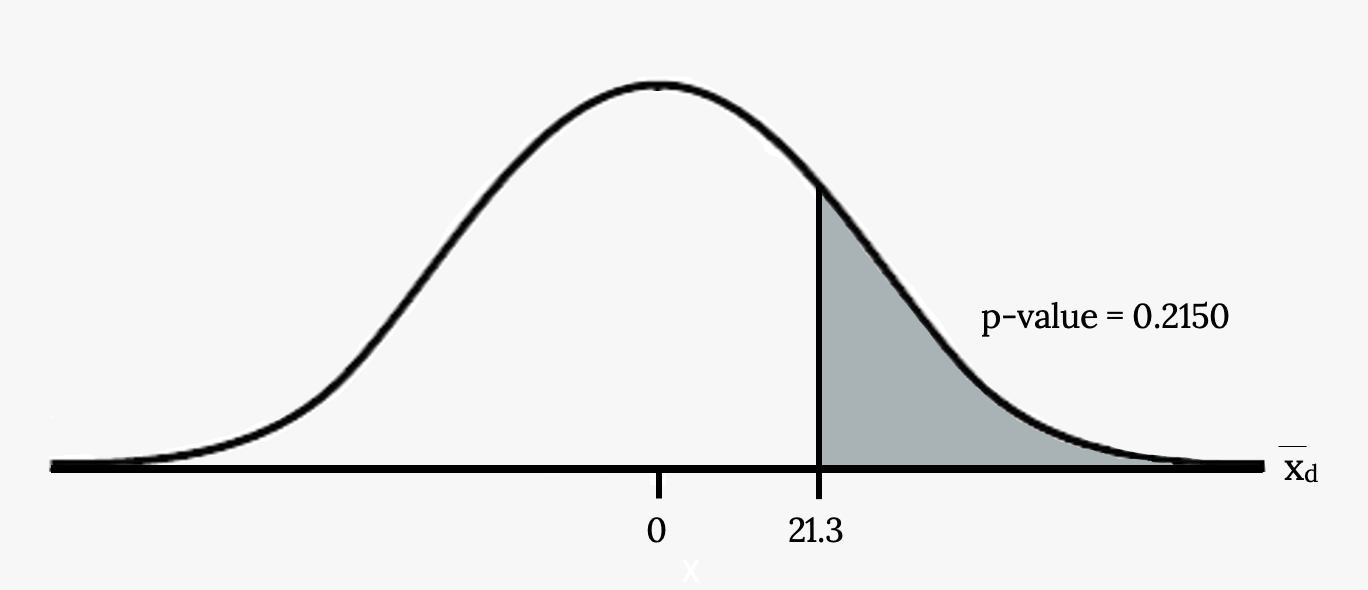
Normal distribution curve with values of 0 and 21.3. A vertical upward line extends from 21.3 to the curve and the p-value is indicated in the area to the right of this value.
Figure 8.6: Weight Lifted P-Value

Calculate the p-value:

Decision:

What is the conclusion?

Your turn!

A new prep class was designed to improve SAT test scores. Five students were selected at random. Their scores on two practice exams were recorded, one before the class and one after. The data recorded in the figure below. Are the scores, on average, higher after the class? Test at a 5% level.

Figure 8.7: SAT Scores
SAT Scores Student 1 Student 2 Student 3 Student 4
Score before class 1840 1960 1920 2150
Score after class 1920 2160 2200 2100

Image Credits

Figure 8.1: Ali Inay (2015). “Brunching with Friends.” Public domain. Retrieved from https://unsplash.com/photos/y3aP9oo9Pjc

Figure 8.3: Kindred Grey via Virginia Tech (2020). “Figure 8.3” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_8.3.png . Adaptation of Figure 5.39 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/5-practice

Figure 8.6: Kindred Grey via Virginia Tech (2020). “Figure 8.6” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_8.6.png . Adaptation of Figure 5.39 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/5-practice

definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Significant Statistics Copyright © 2020 by John Morgan Russell, OpenStaxCollege, OpenIntro is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book