5.4 The Behavior of Confidence Intervals

Once we know the basics of how to calculate a confidence interval, we also need to know how they behave. In other words, how does tweaking certain parts of the equation effect the interval? Keep in mind that one of the criteria that makes something a “good” statistical estimate is precision. A smaller, or more narrow, interval gives us a more precise and therefore useful estimate.

Changing the Confidence Level or Sample Size

Example

Recall the previous example:

Suppose scores on exams in statistics are normally distributed with an unknown population mean and a population standard deviation of three points. A random sample of 36 scores is taken and gives a sample mean score of 68. Find a confidence interval estimate for the population mean exam score (i.e., the mean score on all exams).

Find a 90% confidence interval for the true (population) mean of statistics exam scores.

The 90% confidence interval is (67.1775, 68.8225).

Suppose we change the original problem by using a 95% confidence level. Find a 95% confidence interval for the true (population) mean statistics exam score.

To find the confidence interval, you need \overline{x}, the sample mean, and the MoE.

  • \overline{x} = 68
  • σ = 3; n = 36; the confidence level is 95% (CL = 0.95)
  • MoE = ({z}_{\frac{\alpha }{2}}) (\frac{\sigma }{\sqrt{n}})

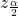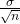Since CL = 0.95, then α = 1 – CL = 1 – 0.95 = 0.05.

\frac{\alpha }{2} = 0.025

{z}_{\frac{\alpha }{2}} = z0.025

The area to the right of z0.025 is 0.025, and the area to the left of z0.025 is 1 – 0.025 = 0.975.

{z}_{\frac{\alpha }{2}} = z0.025 = 1.96

MoE = (1.96)(\frac{3}{\sqrt{36}}) = 0.98

\overline{x} – MoE = 68 – 0.98 = 67.02

\overline{x} + MoE = 68 + 0.98 = 68.98

Notice that the MoE is larger for a 95% confidence level in the original problem, creating a less precise interval.

Interpretation: We estimate with 95% confidence that the true population mean for all statistics exam scores is between 67.02 and 68.98.

Alternative Interpretation

Ninety-five percent of all confidence intervals constructed in this way contain the true value of the population mean statistics exam score. Let’s compare the results:

The 90% confidence interval is (67.18, 68.82), and the 95% confidence interval is (67.02, 68.98). The 95% confidence interval is wider. If you look at the figure below, you’ll see that the area 0.99 is larger than the area 0.90, so it makes sense that the 95% confidence interval is wider. To be more confident that the confidence interval actually does contain the true value of the population mean for all statistics exam scores, it is necessary for the confidence interval to be wider.

Figure description available at the end of the section.
Figure 5.10: Confidence level comparisons. Figure description available at the end of the section.

In conclusion, increasing the confidence level increases the margin of error, making the confidence interval wider.

Working Backwards to Find the Margin of Error or Sample Mean

When we calculate a confidence interval, we must first find the sample mean and calculate the margin of error. However, statistical studies may sometimes state only the confidence interval. If we know the confidence interval, we can work backward to find both the margin of error and the sample mean.

Finding the Margin of Error

  • From the upper value for the interval, subtract the sample mean, or
  • From the upper value for the interval, subtract the lower value, then divide the difference by two.

Finding the Sample Mean

  • Subtract the margin of error from the upper value of the confidence interval, or
  • Average the upper and lower endpoints of the confidence interval.

Notice that there are two methods to perform each calculation. You can choose the method that is easier to use with the information you know.

Example

Suppose we know that a confidence interval is (67.18, 68.82), and we want to find the margin of error. We may know that the sample mean is 68, or perhaps our source only gave the confidence interval and did not tell us the value of the sample mean.

Calculate the margin of error:

  • If we know that the sample mean is 68: MoE = 68.82 – 68 = 0.82.
  • If we don’t know the sample mean: MoE = 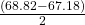\frac{\left(68.82-67.18\right)}{2} = 0.82.

Calculate the sample mean:

  • If we know the margin of error: \overline{x} = 68.82 – 0.82 = 68
  • If we don’t know the margin of error: 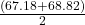\overline{x} = \frac{\left(67.18 + 68.82\right)}{2} = 68.

Your Turn!

Suppose we know that a confidence interval is (42.12, 47.88). Find the margin of error and the sample mean.

Calculating the Sample Size Needed

If researchers desire a specific margin of error, then they can use the margin of error formula to calculate the required sample size.

Recall the margin of error formula for a population mean when the population standard deviation is known:

MoE = ({z}_{\frac{\alpha }{2}}) (\frac{\sigma }{\sqrt{n}})

The formula for sample size is n = \frac{{z}^{2}{\sigma }^{2}}{Mo{E}^{2}}, found by solving the margin of error formula for n.

In this formula, z is {z}_{\frac{\alpha }{2}}, corresponding to the desired confidence level. A researcher planning a study who wants a specified confidence level and margin of error can use this formula to calculate the size of the sample needed for the study.

Example

The population standard deviation for the age of Foothill College students is 15 years. If we want to be 95% confident that the sample mean age is within two years of the true population mean age of Foothill College students, how many randomly selected Foothill College students must be surveyed?

  • From the problem, we know that σ = 15 and MoE = 2.
  • z = z0.025 = 1.96 because the confidence level is 95%.
  • Use the sample size equation: n = 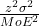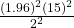\frac{{z}^{2}{\sigma }^{2}}{Mo{E}^{2}} = \frac{{\left(1.96\right)}^{2}{\left(15\right)}^{2}}{{2}^{2}} = 216.09
  • Use n = 217. (Always round the answer up to the next higher integer to ensure that the sample size is large enough.)

Therefore, 217 Foothill College students should be surveyed in order to be 95% confident that we are within two years of the true population mean age of Foothill College students.

Example

The American Community Survey (ACS), part of the United States Census Bureau, conducts a yearly census similar to the one taken every ten years, but with a smaller percentage of participants. The most recent survey estimates with 90% confidence that the mean household income in the US falls between $69,720 and $69,922.[1] Find the point estimate for mean US household income and the margin of error for mean US household income.

The average height of young adult males has a normal distribution with standard deviation of 2.5 inches. You want to estimate the mean height of students at your university to within one inch with 93% confidence. How many male students must you measure?

Use the formula for MoE, solved for n:

n = \frac{{z}^{2}{\sigma }^{2}}{Mo{E}^{2}}

From the statement of the problem, you know that σ = 2.5, and you need MoE = 1.

z = z0.035 = 1.812

(This is the value of z for which the area under the density curve to the right of z is 0.035.)

n = \frac{{z}^{2}{\sigma }^{2}}{Mo{E}^{2}} = \frac{{1.812}^{2}{2.5}^{2}}{{1}^{2}} ≈ 20.52

You need to measure at least 21 male students to achieve your goal.

Your Turn!

The population standard deviation for the height of high school basketball players is three inches. If we want to be 95% confident that the sample mean height is within one inch of the true population mean height, how many randomly selected students must be surveyed?

Additional Resources

QR code

Click here for additional multimedia resources, including podcasts, videos, lecture notes, and worked examples.

If you are using an offline version of this text, access the resources for this section via the QR code, or by visiting https://doi.org/10.7294/26207456.

Figure References

Figure 5.10: Kindred Grey (2024). Confidence level comparisons. CC BY-SA 4.0.

Figure Descriptions

Figure 5.10: Population is larger than the sample. Population mean is slightly above the sample mean. 90% confidence interval: To 90%, the mean value of the population is in this range (x bar + MOE, x bar – MOE). 99% confidence interval has the same formula for finding the range, but is a much wider range. Both intervals include the true population mean, but the 90% interval just barely includes it.

  1. American Fact Finder.” U.S. Census Bureau. Available online at http://factfinder2.census.gov/faces/nav/jsf/pages/searchresults.xhtml?refresh=t (accessed July 2, 2013). ↵

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Significant Statistics: An Introduction to Statistics Copyright © 2024 by John Morgan Russell is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book