Chapter 5 Extra Practice
5.1 Point Estimation and Sampling Distributions
1. The specific absorption rate (SAR) for a cell phone measures the amount of radio frequency (RF) energy absorbed by the user’s body when using the handset. Every cell phone emits RF energy. Different phone models have different SAR measures. To receive certification from the Federal Communications Commission (FCC) for sale in the United States, the SAR level for a cell phone must be no more than 1.6 watts per kilogram. The figure below shows the highest SAR level for a random selection of cell phone models as measured by the FCC.[1] Find a point estimate of the true (population) mean of the specific absorption rates (SARs) for cell phones.
| Phone model | SAR | Phone model | SAR | Phone model | SAR |
|---|---|---|---|---|---|
| Apple iPhone 4S | 1.11 | LG Ally | 1.36 | Pantech Laser | 0.74 |
| BlackBerry Pearl 8120 | 1.48 | LG AX275 | 1.34 | Samsung Character | 0.5 |
| BlackBerry Tour 9630 | 1.43 | LG Cosmos | 1.18 | Samsung Epic 4G Touch | 0.4 |
| Cricket TXTM8 | 1.3 | LG CU515 | 1.3 | Samsung M240 | 0.867 |
| HP/Palm Centro | 1.09 | LG Trax CU575 | 1.26 | Samsung Messager III SCH-R750 | 0.68 |
| HTC One V | 0.455 | Motorola Q9h | 1.29 | Samsung Nexus S | 0.51 |
| HTC Touch Pro 2 | 1.41 | Motorola Razr2 V8 | 0.36 | Samsung SGH-A227 | 1.13 |
| Huawei M835 Ideos | 0.82 | Motorola Razr2 V9 | 0.52 | SGH-a107 GoPhone | 0.3 |
| Kyocera DuraPlus | 0.78 | Motorola V195s | 1.6 | Sony W350a | 1.48 |
| Kyocera K127 Marbl | 1.25 | Nokia 1680 | 1.39 | T-Mobile Concord | 1.38 |
Figure 5.15
2. A student polls his school to see if students in the school district are for or against the new legislation regarding school uniforms. She surveys 600 students and finds that 480 are against the new legislation. Find a point estimate of the true (population) proportion of students in the school district who are against the new legislation.
5.2 The Sampling Distribution of the Sample Mean (CLT)
1. The length of time, in hours, it takes an “over 40” group of people to play one soccer match is normally distributed with a mean of two hours and a standard deviation of 0.5 hours. A sample of size n = 50 is drawn randomly from the population. Find the probability that the sample mean is between 1.8 hours and 2.3 hours.
- Let X = the time, in hours, it takes to play one soccer match.
- The probability question asks you to find a probability for the sample mean time, in hours, it takes to play one soccer match.
- Let
 = the mean time, in hours, it takes to play one soccer match.
= the mean time, in hours, it takes to play one soccer match.
- If μX = , σX = , and n = , then X ~ N( , ) by the central limit theorem for means.
- Find P(1.8 <
 < 2.3). Draw a graph.
< 2.3). Draw a graph.
2. The length of time taken on the SAT for a group of students is normally distributed with a mean of 2.5 hours and a standard deviation of 0.25 hours.[2] A sample size of n = 60 is drawn randomly from the population. Find the probability that the sample mean is between two hours and three hours.
3. In a recent study reported Oct. 29, 2012, on the Flurry Blog, the mean age of tablet users is 34 years.[3] Suppose the standard deviation is 15 years. Take a sample of size n = 100.
- What are the mean and standard deviation for the sample mean ages of tablet users?
- What does the distribution look like?
- Find the probability that the sample mean age is more than 34 years (the reported mean age of tablet users in this particular study).
- Find the 95th percentile for the sample mean age (to one decimal place).
4. An article on Flurry Blog identified a gaming marketing gap for men between the ages of 30 and 40.[4] You are researching a startup game targeted at the 35-year-old demographic. Your idea is to develop a strategy game that can be played by men from their late 20s through their late 30s. Based on the article’s data, industry research shows that the average strategy player is 28 years old with a standard deviation of 4.8 years. You take a sample of 100 randomly selected gamers. If your target market is 29- to 35-year-olds, should you continue with your development strategy?
5. Cans of a cola beverage claim to contain 16 ounces. The amounts in a sample are measured, and the statistics are n = 34 and ![]() = 16.01 ounces. If the cans are filled so that μ = 16.00 ounces (as labeled) and σ = 0.143 ounces, find the probability that a sample of 34 cans will have an average amount greater than 16.01 ounces. Do the results suggest that cans are filled with an amount greater than 16 ounces?
= 16.01 ounces. If the cans are filled so that μ = 16.00 ounces (as labeled) and σ = 0.143 ounces, find the probability that a sample of 34 cans will have an average amount greater than 16.01 ounces. Do the results suggest that cans are filled with an amount greater than 16 ounces?
6. Yoonie is a personnel manager in a large corporation. Each month, she must review 16 of the employees. From past experience, she has found that the reviews each take her approximately four hours to do with a population standard deviation of 1.2 hours. Let X be the random variable representing the time it takes her to complete one review. Assume X is normally distributed. Let ![]() be the random variable representing the mean time to complete the 16 reviews. Assume that the 16 reviews represent a random set of reviews.
be the random variable representing the mean time to complete the 16 reviews. Assume that the 16 reviews represent a random set of reviews.
- What is the mean, standard deviation, and sample size?
- Complete the distributions for X and
 .
. - Find the probability that one review will take Yoonie from 3.5 to 4.25 hours. Sketch a graph, labeling and scaling the horizontal axis. Shade the region corresponding to the probability.
- Find the probability that the mean of a month’s reviews will take Yoonie from 3.5 to 4.25 hrs. Sketch a graph, labeling and scaling the horizontal axis. Shade the region corresponding to the probability.
- What causes the probabilities in C and D to be different?
- Find the 95th percentile for the mean time to complete one month’s reviews. Sketch the graph.
7. Previously, De Anza statistics students estimated that the amount of change carried by daytime statistics students is exponentially distributed with a mean of 88 cents. Suppose that we randomly pick 25 daytime statistics students.
- In words, X =
- X ~ ( , )
- In words,
 =
=  ~ ( , )
~ ( , )- Find the probability that an individual had between $0.80 and $1.00. Graph the situation, and shade in the area to be determined.
- Find the probability that the average of the 25 students was between $0.80 and $1.00. Graph the situation, and shade in the area to be determined.
- Explain why there is a difference in part (e) and (f).
8. Suppose that the distance of fly balls hit to the outfield (in baseball) is normally distributed with a mean of 250 feet and a standard deviation of 50 feet. We randomly sample 49 fly balls.
- If
 = average distance in feet for 49 fly balls, then
= average distance in feet for 49 fly balls, then  ~ ( , )
~ ( , ) - What is the probability that the 49 balls traveled an average of less than 240 feet? Sketch the graph. Scale the horizontal axis for
 . Shade the region corresponding to the probability. Find the probability.
. Shade the region corresponding to the probability. Find the probability. - Find the 80th percentile of the distribution of the average of 49 fly balls.
9. According to the Internal Revenue Service, the average length of time for an individual to complete (keep records for, learn, prepare, copy, assemble, and send) IRS Form 1040 is 10.53 hours (without any attached schedules). The distribution is unknown. Let us assume that the standard deviation is two hours. Suppose we randomly sample 36 taxpayers.
- In words, X =
- In words,
 =
=  ~ ( , )
~ ( , )- Would you be surprised if the 36 taxpayers finished their form 1040s in an average of more than 12 hours? Explain why or why not in complete sentences.
- Would you be surprised if one taxpayer finished their form 1040 in more than 12 hours? In a complete sentence, explain why.
10. Suppose that a category of world-class runners are known to run a marathon (26.2 miles) in an average of 145 minutes with a standard deviation of 14 minutes. Consider 49 of the races. Let ![]() the average of the 49 races.
the average of the 49 races.
 ~ ( , )
~ ( , )- Find the probability that the runner will average between 142 and 146 minutes in these 49 marathons.
- Find the 80th percentile for the average of these 49 marathons.
- Find the median of the average running times.
11. The length of songs in a collector’s iTunes album collection is uniformly distributed from two to 3.5 minutes. Suppose we randomly pick five albums from the collection. There are a total of 43 songs on the five albums.
- In words, X =
- X ~
- In words,
 =
=  ~ ( , )
~ ( , )- Find the first quartile for the average song length,
 .
. - The IQR (interquartile range) for the average song length,
 , is from – .
, is from – .
12. In 1940, the average size of a US farm was 174 acres.[5] Let’s say that the standard deviation was 55 acres. Suppose we randomly survey 38 farmers from 1940.
- In words, X =
- In words,
 =
=  ~ ( , )
~ ( , )- The IQR for
 is from acres to acres.
is from acres to acres.
13. Determine which of the following are true and which are false. Then, in complete sentences, justify your answers.
- When the sample size is large, the mean of
 is approximately equal to the mean of X.
is approximately equal to the mean of X. - When the sample size is large,
 is approximately normally distributed.
is approximately normally distributed. - When the sample size is large, the standard deviation of
 is approximately the same as the standard deviation of X.
is approximately the same as the standard deviation of X.
14. The percent of fat calories that a person in America consumes each day is normally distributed with a mean of about 36 and a standard deviation of about ten.[6] Suppose that 16 individuals are randomly chosen. Let ![]() = average percent of fat calories.
= average percent of fat calories.
 ~ ( , )
~ ( , )- For the group of 16, find the probability that the average percent of fat calories consumed is more than five. Graph the situation and shade in the area to be determined.
- Find the first quartile for the average percent of fat calories.
15. The distribution of income in some Third World countries is considered wedge-shaped (many very poor people, very few middle income people, and even fewer wealthy people). Suppose we pick a country with a wedge-shaped distribution. Let the average salary be $2,000 per year with a standard deviation of $8,000. We randomly survey 1,000 residents of that country.
- In words, X =
- In words,
 =
=  ~ ( , )
~ ( , )- How is it possible for the standard deviation to be greater than the average?
- Why is it more likely that the average of the 1,000 residents will be from $2,000 to $2,100 than from $2,100 to $2,200?
16. Which of the following is NOT TRUE about the distribution for averages?
- The mean, median, and mode are equal.
- The area under the curve is one.
- The curve never touches the x-axis.
- The curve is skewed to the right.
17. The cost of unleaded gasoline in the Bay Area once followed an unknown distribution with a mean of $4.59 cents and a standard deviation of 10 cents. Sixteen gas stations from the Bay Area are randomly chosen. We are interested in the average cost of gasoline for the 16 gas stations. The distribution to use for the average cost of gasoline for the 16 gas stations is:
 ~ N(4.59, 0.10)
~ N(4.59, 0.10) ~ N(4.59,
~ N(4.59, 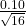 )
) ~ N(4.59,
~ N(4.59, 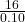 )
) ~ N(4.59,
~ N(4.59, 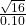 )
)
5.3 Introduction to Confidence Intervals
1. The specific absorption rate (SAR) for a cell phone measures the amount of radio frequency (RF) energy absorbed by the user’s body when using the handset. Every cell phone emits RF energy. Different phone models have different SAR measures. To receive certification from the Federal Communications Commission (FCC) for sale in the United States, the SAR level for a cell phone must be no more than 1.6 watts per kilogram. The figure below shows the highest SAR level for a random selection of cell phone models as measured by the FCC.[7] Find a 98% confidence interval for the true (population) mean of the specific absorption rates (SARs) for cell phones. Assume that the population standard deviation is σ = 0.337.
| Phone model | SAR | Phone model | SAR | Phone model | SAR |
|---|---|---|---|---|---|
| Apple iPhone 4S | 1.11 | LG Ally | 1.36 | Pantech Laser | 0.74 |
| BlackBerry Pearl 8120 | 1.48 | LG AX275 | 1.34 | Samsung Character | 0.5 |
| BlackBerry Tour 9630 | 1.43 | LG Cosmos | 1.18 | Samsung Epic 4G Touch | 0.4 |
| Cricket TXTM8 | 1.3 | LG CU515 | 1.3 | Samsung M240 | 0.867 |
| HP/Palm Centro | 1.09 | LG Trax CU575 | 1.26 | Samsung Messager III SCH-R750 | 0.68 |
| HTC One V | 0.455 | Motorola Q9h | 1.29 | Samsung Nexus S | 0.51 |
| HTC Touch Pro 2 | 1.41 | Motorola Razr2 V8 | 0.36 | Samsung SGH-A227 | 1.13 |
| Huawei M835 Ideos | 0.82 | Motorola Razr2 V9 | 0.52 | SGH-a107 GoPhone | 0.3 |
| Kyocera DuraPlus | 0.78 | Motorola V195s | 1.6 | Sony W350a | 1.48 |
| Kyocera K127 Marbl | 1.25 | Nokia 1680 | 1.39 | T-Mobile Concord | 1.38 |
Figure 5.16
2. The figure below shows a different random sampling of 20 cell phone models. Use this data to calculate a 93% confidence interval for the true mean SAR for cell phones certified for use in the United States.[8] As previously, assume that the population standard deviation is σ = 0.337.
| Phone model | SAR | Phone model | SAR |
|---|---|---|---|
| BlackBerry Pearl 8120 | 1.48 | Nokia E71x | 1.53 |
| HTC Evo Design 4G | 0.8 | Nokia N75 | 0.68 |
| HTC Freestyle | 1.15 | Nokia N79 | 1.4 |
| LG Ally | 1.36 | Sagem Puma | 1.24 |
| LG Fathom | 0.77 | Samsung Fascinate | 0.57 |
| LG Optimus Vu | 0.462 | Samsung Infuse 4G | 0.2 |
| Motorola Cliq XT | 1.36 | Samsung Nexus S | 0.51 |
| Motorola Droid Pro | 1.39 | Samsung Replenish | 0.3 |
| Motorola Droid Razr M | 1.3 | Sony W518a Walkman | 0.73 |
| Nokia 7705 Twist | 0.07 | ZTE C79 | 0.869 |
Figure 5.17
3. The standard deviation of the weights of elephants is known to be approximately 15 pounds. We wish to construct a 95% confidence interval for the mean weight of newborn elephant calves. Fifty newborn elephants are weighed. The sample mean is 244 pounds. The sample standard deviation is 11 pounds.
- Identify the following:

- σ
- n
- In words, define the random variables X and
 .
. - Which distribution should you use for this problem?
- Construct a 95% confidence interval for the population mean weight of newborn elephants. State the confidence interval, sketch the graph, and calculate the margin of error.
- What will happen to the confidence interval obtained if 500 newborn elephants are weighed instead of 50? Why?
4. The U.S. Census Bureau conducts a study to determine the time needed to complete the short form. The Bureau surveys 200 people. The sample mean is 8.2 minutes. There is a known standard deviation of 2.2 minutes. The population distribution is assumed to be normal.[9]
- Identify the following:

- σ
- n
- In words, define the random variables X and
 .
. - Which distribution should you use for this problem?
- Construct a 90% confidence interval for the population mean time to complete the forms. State the confidence interval, sketch the graph, and calculate the margin of error.
- If the Census wants to increase its level of confidence and keep the margin of error the same by taking another survey, what changes should it make?
- If the Census did another survey, kept the margin of error the same, and surveyed only 50 people instead of 200, what would happen to the level of confidence? Why?
- Suppose the Census needed to be 98% confident of the population mean length of time. Would the Census have to survey more people? Why or why not?
5. A sample of 20 heads of lettuce was selected. Assume that the population distribution of head weight is normal. The weight of each head of lettuce was then recorded. The mean weight was 2.2 pounds with a standard deviation of 0.1 pounds. The population standard deviation is known to be 0.2 pounds.
- Identify the following:

- σ
- n
- In words, define the random variable X.
- In words, define the random variable
 .
. - Which distribution should you use for this problem?
- Construct a 90% confidence interval for the population mean weight of the heads of lettuce. State the confidence interval, sketch the graph, and calculate the margin of error.
- Construct a 95% confidence interval for the population mean weight of the heads of lettuce. State the confidence interval, sketch the graph, and calculate the margin of error.
- In complete sentences, explain why the confidence interval in (f) is larger than in (e).
- In complete sentences, give an interpretation of what the interval in (e) means.
- What would happen if 40 heads of lettuce were sampled instead of 20 and the margin of error remained the same?
- What would happen if 40 heads of lettuce were sampled instead of 20 and the confidence level remained the same?
6. The mean age for all Foothill College students for a recent fall term was 33.2. The population standard deviation has been pretty consistent at 15. Suppose that 25 winter students were randomly selected. The mean age for the sample was 30.4. We are interested in the true mean age for winter Foothill College students.[10] Let X = the age of a winter Foothill College student.
- Identify
 .
. - Identify n.
- What variable does 15 represent?
- In words, define the random variable
 .
. - What is
 estimating?
estimating? - Is
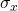 known?
known? - As a result of your answer to (e), state the exact distribution to use when calculating the confidence interval.
- Construct a 95% confidence interval for the true mean age of winter Foothill College students by working out (i)-(o).
- How much area is in both tails (combined)? α =
- How much area is in each tail?
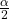 =
= - Identify the following specifications:
- lower limit
- upper limit
- margin of error
- The 95% confidence interval is: .
- Fill in the blanks on the graph with the areas, upper and lower limits of the confidence interval, and the sample mean.
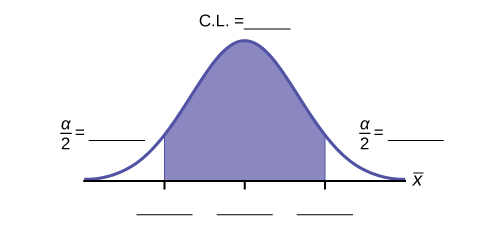
Figure 5.18. Figure description available at the end of the section. - In one complete sentence, explain what the interval means.
- Using the same mean, standard deviation, and level of confidence, suppose that n were 69 instead of 25. Would the margin of error become larger or smaller? How do you know?
7. Among various ethnic groups, the standard deviation of heights is known to be approximately three inches. We wish to construct a 95% confidence interval for the mean height of male Swedes. Forty-eight male Swedes are surveyed. The sample mean is 71 inches. The sample standard deviation is 2.8 inches.
- Identify
 .
. - Identify σ.
- Identify n.
- In words, define the random variables X and
 .
. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population mean height of male Swedes.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- What will happen to the level of confidence obtained if 1,000 male Swedes are surveyed instead of 48? Why?
- 71
- 3
- 48
8. Announcements for 84 upcoming engineering conferences were randomly picked from a stack of IEEE Spectrum magazines. The mean length of the conferences was 3.94 days with a standard deviation of 1.28 days. Assume the underlying population is normal.
- In words, define the random variables X and
 .
. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population mean length of engineering conferences.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
9. Suppose that an accounting firm does a study to determine the time needed to complete one person’s tax forms. It randomly surveys 100 people. The sample mean is 23.6 hours. There is a known standard deviation of 7.0 hours. The population distribution is assumed to be normal.
- Identify the following:
 =
= - σ =
- n =
- In words, define the random variables X and
 .
. - Which distribution should you use for this problem? Explain your choice.
- Construct a 90% confidence interval for the population mean time to complete the tax forms.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- If the firm wished to increase its level of confidence and keep the margin of error the same by taking another survey, what changes should it make?
- If the firm did another survey, kept the margin of error the same, and only surveyed 49 people, what would happen to the level of confidence? Why?
- Suppose that the firm decided that it needed to be at least 96% confident of the population mean length of time to within one hour. How would the number of people the firm surveys change? Why?
10. A sample of 16 small bags of the same brand of candies was selected. Assume that the population distribution of bag weights is normal. The weight of each bag was then recorded. The mean weight was two ounces with a standard deviation of 0.12 ounces. The population standard deviation is known to be 0.1 ounce.
- Identify the following:
 =
= - σ =
- sx =
- In words, define the random variable X.
- In words, define the random variable
 .
. - Which distribution should you use for this problem? Explain your choice.
- Construct a 90% confidence interval for the population mean weight of the candies.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- Construct a 98% confidence interval for the population mean weight of the candies.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- In complete sentences, explain why the confidence interval in (f) is larger than the confidence interval in (e).
- In complete sentences, give an interpretation of what the interval in f) means.
11. A camp director is interested in the mean number of letters each child sends during their camp session. The population standard deviation is known to be 2.5. A survey of 20 campers is taken. The mean from the sample is 7.9 with a sample standard deviation of 2.8.
- Identify the following:
 =
= - σ =
- n =
- Define the random variables X and
 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 90% confidence interval for the population mean number of letters campers send home.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- What will happen to the margin of error and confidence interval if 500 campers are surveyed? Why?
12. What is meant by the term “90% confident” when constructing a confidence interval for a mean?
- If we took repeated samples, approximately 90% of the samples would produce the same confidence interval.
- If we took repeated samples, approximately 90% of the confidence intervals calculated from those samples would contain the sample mean.
- If we took repeated samples, approximately 90% of the confidence intervals calculated from those samples would contain the true value of the population mean.
- If we took repeated samples, the sample mean would equal the population mean in approximately 90% of the samples.
13. The Federal Election Commission collects information about campaign contributions and disbursements for candidates and political committees each election cycle. During the 2012 campaign season, there were 1,619 candidates for the House of Representatives across the United States who received contributions from individuals. The figure below shows the total receipts from individuals for a random selection of 40 House candidates rounded to the nearest $100. The standard deviation for this data to the nearest hundred is σ = $909,200.
| Receipts | ||||
|---|---|---|---|---|
| $3,600 | $1,243,900 | $10,900 | $385,200 | $581,500 |
| $7,400 | $2,900 | $400 | $3,714,500 | $632,500 |
| $391,000 | $467,400 | $56,800 | $5,800 | $405,200 |
| $733,200 | $8,000 | $468,700 | $75,200 | $41,000 |
| $13,300 | $9,500 | $953,800 | $1,113,500 | $1,109,300 |
| $353,900 | $986,100 | $88,600 | $378,200 | $13,200 |
| $3,800 | $745,100 | $5,800 | $3,072,100 | $1,626,700 |
| $512,900 | $2,309,200 | $6,600 | $202,400 | $15,800 |
Figure 5.19
- Find the point estimate for the population mean.
- Using 95% confidence, calculate the margin of error.
- Create a 95% confidence interval for the mean total individual contributions.
- Interpret the confidence interval in the context of the problem.
5.4 The Behavior of Confidence Intervals
1. Suppose average pizza delivery times are normally distributed with an unknown population mean and a population standard deviation of 6 minutes. A random sample of 28 pizza delivery restaurants is taken and has a sample mean delivery time of 36 min.
The population standard deviation is six minutes, and the sample mean delivery time is 36 minutes. Use a sample size of 20. Find a 95% confidence interval estimate for the true mean pizza delivery time.
2. What happens to the margin of error in the pizza-delivery exercise if the sample size is changed? Leave everything the same except the sample size. Use the original 90% confidence level.
- What happens to the margin of error and the confidence interval if we increase the sample size and use n = 100 instead of n = 36?
- What happens if we decrease the sample size to n = 25 instead of n = 36?
 = 68
= 68- EBM =
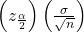
- σ = 3; the confidence level is 90% (CL = 0.90);
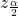 = z0.05 = 1.645.
= z0.05 = 1.645.
3. Refer back to the pizza-delivery exercise. The mean delivery time is 36 minutes, and the population standard deviation is six minutes. Assume the sample size is changed to 50 restaurants with the same sample mean. Find a 90% confidence interval estimate for the population mean delivery time.
5.5 Introduction to Hypothesis Tests
1. When do you reject the null hypothesis?
2. The probability of winning the grand prize at a particular carnival game is 0.005. Is the outcome of winning very likely or very unlikely?
3. It is believed that the mean height of high school students who play basketball on the school team is 73 inches with a standard deviation of 1.8 inches. A random sample of 40 players is chosen. The sample mean was 71 inches, and the sample standard deviation was 1.5 years. Do the data support the claim that the mean height is less than 73 inches? The p-value is almost zero. State the null and alternative hypotheses, and interpret the p-value.
4. The mean age of graduate students at a university is at most 31 years with a standard deviation of two years. A random sample of 15 graduate students is taken. The sample mean is 32 years, and the sample standard deviation is three years. Are the data significant at the 1% level? The p-value is 0.0264. State the null and alternative hypotheses and interpret the p-value.
5. Does the shaded region represent a low or a high p-value compared to a level of significance of 1%?
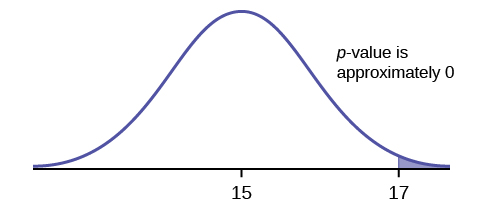
6. What should you do when α > p-value?
7. What should you do if α = p-value?
8. If you do not reject the null hypothesis, then it must be true. Is this statement correct? State why or why not in complete sentences.
9. Suppose that a recent article stated that the mean time spent in jail by a first-time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was three years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. Conduct a hypothesis test to determine if the mean length of jail time has increased. Assume the distribution of the jail times is approximately normal.
- Is this a test of means or proportions?
- What symbol represents the random variable for this test?
- In words, define the random variable for this test.
- Is σ known, and if so, what is it?
- Calculate the following:

- σ
- sx
- n
- Since both σ and
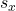 are given, which should be used? In one to two complete sentences, explain why.
are given, which should be used? In one to two complete sentences, explain why. - State the distribution to use for the hypothesis test.
10. A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. Conduct a hypothesis test to determine if the population mean time on death row could likely be 15 years.
- Is this a test of one mean or proportion?
- State the null and alternative hypotheses.
H0:
Ha : - Is this a right-tailed, left-tailed, or two-tailed test?
- What symbol represents the random variable for this test?
- In words, define the random variable for this test.
- Is the population standard deviation known, and if so, what is it?
- Calculate the following:
 =
= - s =
- n =
- Which test should be used?
- State the distribution to use for the hypothesis test.
- Find the p-value.
- At a pre-conceived α = 0.05, what is your:
- Decision
- Reason for the decision
- Conclusion (write out in a complete sentence)
11. The National Institute of Mental Health published an article stating that, in any one-year period, approximately 9.5% of American adults suffer from depression or a depressive illness.[11] Suppose that a survey of 100 people in a certain town found that seven of them suffered from depression or a depressive illness. Conduct a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population.
- Is this a test of one mean or proportion?
- State the null and alternative hypotheses.
H0:
Ha: - Is this a right-tailed, left-tailed, or two-tailed test?
- What symbol represents the random variable for this test?
- In words, define the random variable for this test.
- Calculate the following:
- x =
- n =
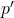 =
=
- Calculate σx = . Show the formula set-up.
- State the distribution to use for the hypothesis test.
- Find the p-value.
- At a pre-conceived α = 0.05, what is your:
- Decision
- Reason for the decision
- Conclusion (write out in a complete sentence)
12. We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H0: μ 66
- Ha: μ 66
13. We want to test if college students take less than five years to graduate from college, on the average. State the null and alternative hypotheses.
14. We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H0: μ 45
- Ha: μ 45
15. In an issue of U.S. News & World Report, an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of US students take advanced placement exams and 4.4% pass. Test if the percentage of US students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
16. On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H0: p 0.40
- Ha: p 0.40
17. You are testing that the mean speed of your cable Internet connection is more than three megabits per second. What is the random variable? Describe in words.
18. You are testing that the mean speed of your cable Internet connection is more than three megabits per second. State the null and alternative hypotheses.
19. The American family has an average of two children. What is the random variable? Describe in words.
20. The mean entry level salary of an employee at a company is $58,000. You believe it is higher for IT professionals in the company. State the null and alternative hypotheses.
21. A sociologist claims the probability that a person picked at random in Times Square in New York City is a visitor to the area is 0.83. You want to test to see if the proportion is actually less. What is the random variable? Describe in words.
22. A sociologist claims the probability that a person picked at random in Times Square in New York City is a visitor to the area is 0.83. You want to test to see if the claim is correct. State the null and alternative hypotheses.
23. In a population of fish, approximately 42% are female. A test is conducted to see if the proportion is actually less. State the null and alternative hypotheses.
24. Suppose that a recent article stated that the mean time spent in jail by a first–time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be? The distribution of the population is normal.
- H0:
- Ha:
25. A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. If you were conducting a hypothesis test to determine if the population mean time on death row could likely be 15 years, what would the null and alternative hypotheses be?
- H0:
- Ha:
26. The National Institute of Mental Health published an article stating that, in any one-year period, approximately 9.5% of American adults suffer from depression or a depressive illness.[12] Suppose that a survey of 100 people in a certain town found that 7 of them suffered from depression or a depressive illness. If you were conducting a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population, what would the null and alternative hypotheses be?
- H0:
- Ha:
27. Some of the following statements refer to the null hypothesis, some to the alternate hypothesis. State the null hypothesis, H0, and the alternative hypothesis, Ha, in terms of the appropriate parameter (μ or p).
- The mean number of years Americans work before retiring is 34.
- At most 60% of Americans vote in presidential elections.
- The mean starting salary for San Jose State University graduates is at least $100,000 per year.
- Twenty-nine percent of high school seniors get drunk each month.
- Fewer than 5% of adults ride the bus to work in Los Angeles.
- The mean number of cars a person owns in her lifetime is not more than ten.
- About half of Americans prefer to live away from cities, given the choice.
- Europeans have a mean paid vacation each year of six weeks.
- The chance of developing breast cancer is under 11% for women.
- Private universities’ mean tuition cost is more than $20,000 per year.
28. Over the past few decades, public health officials have examined the link between weight concerns and teen girls’ smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years, the girls were surveyed again. 63 said they smoked to stay thin. Is there good evidence that more than 30% of the teen girls smoke to stay thin? The alternative hypothesis is:
- p < 0.30
- p ≤ 0.30
- p ≥ 0.30
- p > 0.30
29. A statistics instructor believes that fewer than 20% of Evergreen Valley College students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:
- p = 0.20
- p > 0.20
- p < 0.20
- p ≤ 0.20
30. Previously, an organization reported that teenagers spent an average of 4.5 hours on the phone each week. The organization thinks that the mean is currently higher. 15 randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:
- Ho:
 = 4.5; Ha:
= 4.5; Ha:  > 4.5
> 4.5 - Ho: μ ≥ 4.5; Ha: μ < 4.5
- Ho: μ = 4.75; Ha: μ > 4.75
- Ho: μ = 4.5; Ha: μ > 4.5
5.6 Hypothesis Tests in Depth
1. Suppose the null hypothesis, H0, is: the victim of an automobile accident is alive when he arrives at the emergency room of a hospital.
- Type I error: The emergency crew thinks that the victim is dead when, in fact, the victim is alive.
- Type II error: The emergency crew does not know if the victim is alive when, in fact, the victim is dead.
- α = probability that the emergency crew thinks the victim is dead when, in fact, he is really alive = P(type I error).
- β = probability that the emergency crew does not know if the victim is alive when, in fact, the victim is dead = P(type II error).
Which is the error with the greater consequence?
2. Suppose the null hypothesis, H0, is: a patient is not sick. Which type of error has the greater consequence, type I or type II?
3. It’s a Boy Genetic Labs claim to be able to increase the likelihood that a pregnancy will result in a boy being born. Statisticians want to test the claim. Suppose that the null hypothesis, H0, is: It’s a Boy Genetic Labs has no effect on gender outcome.
- Type I error: This results when a true null hypothesis is rejected. In the context of this scenario, we would state that we believe that It’s a Boy Genetic Labs influences the gender outcome, when it actually has no effect. The probability of this error occurring is denoted by the Greek letter alpha, α.
- Type II error: This results when we fail to reject a false null hypothesis. In context, we would state that It’s a Boy Genetic Labs does not influence the gender outcome of a pregnancy when, in fact, it does. The probability of this error occurring is denoted by the Greek letter beta, β.
What is the error of greater consequence?
4. Red tide is a bloom of poison-producing algae composed of a few different species of a class of plankton called dinoflagellates. When the weather and water conditions cause these blooms, shellfish such as clams living in the area develop dangerous levels of a paralysis-inducing toxin. In Massachusetts, the Division of Marine Fisheries (DMF) monitors levels of the toxin in shellfish by regularly sampling shellfish along the coastline. If the mean level of toxin in clams exceeds 800 μg (micrograms) of toxin per kg of clam meat in any area, clam harvesting is banned there until the bloom is over and levels of toxin in clams subside. Describe both a type I and a type II error in this context, and state which error has the greater consequence.
5. A certain experimental drug claims a cure rate of at least 75% for males with prostate cancer. Describe both the type I and type II errors in context. Which error is the more serious?
- Type I: A cancer patient believes the cure rate for the drug is less than 75% when it actually is at least 75%.
- Type II: A cancer patient believes the experimental drug has at least a 75% cure rate when it has a cure rate that is less than 75%.
6. Determine both type I and type II errors for the following scenario:
Assume a null hypothesis, H0, that states the percentage of adults with jobs is at least 88%.
7. Identify the type I and type II errors from these four statements:
- Do not reject the null hypothesis that the percentage of adults who have jobs is at least 88% when that percentage is actually less than 88%.
- No not reject the null hypothesis that the percentage of adults who have jobs is at least 88% when the percentage is actually at least 88%.
- Reject the null hypothesis that the percentage of adults who have jobs is at least 88% when the percentage is actually at least 88%.
- Reject the null hypothesis that the percentage of adults who have jobs is at least 88% when that percentage is actually less than 88%.
8. The mean price of mid-sized cars in a region is $32,000. A test is conducted to see if the claim is true. State the type I and type II errors in complete sentences.
9. A sleeping bag is tested to withstand temperatures of –15°F. You think the bag cannot stand temperatures that low. State the type I and type II errors in complete sentences.
10. A group of doctors is deciding whether or not to perform an operation. Suppose the null hypothesis, H0, is: the surgical procedure will go well. State the Type I and Type II errors in complete sentences. Which is the error with the greater consequence?
11. The power of a test is 0.981. What is the probability of a type II error?
12. A group of divers is exploring an old sunken ship. Suppose the null hypothesis, H0, is: the sunken ship does not contain buried treasure. State the type I and type II errors in complete sentences.
13. A microbiologist is testing a water sample for E. coli. Suppose the null hypothesis, H0, is: the sample does not contain E. coli. The probability that the sample does not contain E. coli while the microbiologist thinks it does is 0.012. The probability that the sample does contain E. coli while the microbiologist thinks it does not is 0.002. What is the power of this test?
14. A microbiologist is testing a water sample for E. coli. Suppose the null hypothesis, H0, is: the sample contains E. coli. Which is the error with the greater consequence?
15. State the type I and type II errors in complete sentences given the following statements.
- The mean number of years Americans work before retiring is 34.
- At most 60% of Americans vote in presidential elections.
- The mean starting salary for San Jose State University graduates is at least $100,000 per year.
- Twenty-nine percent of high school seniors get drunk each month.
- Fewer than 5% of adults ride the bus to work in Los Angeles.
- The mean number of cars a person owns in their lifetime is not more than ten.
- About half of Americans prefer to live away from cities, given the choice.
- Europeans have a mean paid vacation each year of six weeks.
- The chance of developing breast cancer is under 11% for women.
- Private universities mean tuition cost is more than $20,000 per year.
16. For statements (a) through (j) in the previous question, answer each of the following in complete sentences.
- State a consequence of committing a type I error.
- State a consequence of committing a type II error.
17. When a new drug is created, the pharmaceutical company must subject it to testing before receiving the necessary permission from the Food and Drug Administration to market the drug. Suppose the null hypothesis is “the drug is unsafe.” What is the type II error?
- To conclude the drug is safe, when in fact, it is unsafe.
- Not to conclude the drug is safe, when in fact, it is safe.
- To conclude the drug is safe, when in fact, it is safe.
- Not to conclude the drug is unsafe, when in fact, it is unsafe.
18. A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 of them attended the midnight showing. The type I error is to conclude that the percent of EVC students who attended is .
- At least 20%, when in fact, it is less than 20%
- 20%, when in fact, it is 20%
- Less than 20%, when in fact, it is at least 20%
- Less than 20%, when in fact, it is less than 20%
19. It is believed that Lake Tahoe Community College (LTCC) Intermediate Algebra students get less than seven hours of sleep per night, on average. A survey of 22 LTCC Intermediate Algebra students generated a mean of 7.24 hours with a standard deviation of 1.93 hours.[13] At a level of significance of 5%, do LTCC Intermediate Algebra students get less than seven hours of sleep per night, on average?
The type II error is not to reject that the mean number of hours of sleep LTCC students get per night is at least seven, when in fact, the mean number of hours is .
- More than seven hours
- At most seven hours
- At least seven hours
- Less than seven hours
20. Previously, an organization reported that teenagers spent an average of 4.5 hours on the phone each week. The organization thinks that the mean is currently higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The type I error is:
- To conclude that the current mean hours per week is higher than 4.5, when in fact, it is higher.
- To conclude that the current mean hours per week is higher than 4.5, when in fact, it is the same.
- To conclude that the current mean hours per week is 4.5, when in fact, it is higher.
- To conclude that the current mean hours per week is no higher than 4.5, when in fact, it is not higher.
Figure Descriptions
Figure 5.18: This is a template of a normal distribution curve with the central region shaded to represent a confidence interval. The residual areas are on either side of the shaded region. Blanks indicate that students should label the confidence level, residual areas, and points that define the confidence interval.
Figure 5.20: Normal distribution curve with one vertical upward line from x-axis to curve on the far right of the curve. From this line to the right is shaded under the curve. The mean is labeled with a value of 15, and the vertical line to the right of it is labeled with a value of 17. Above the curve reads ‘p-value is approximately 0.’
References
Figures
Figure 5.18: Figure 8.8 from OpenStax Introductory Statistics 2e (2023) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics-2e/pages/8-practice#element-158
Figure 5.20: Figure 9.18 from OpenStax Introductory Statistics 2e (2023) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics-2e/pages/9-practice
Text
Baran, Daya. “20 Percent of Americans Have Never Used Email.” WebGuild, 2010. Available online at http://www.webguild.org/20080519/20-percent-of-americans-have-never-used-email (accessed May 17, 2013).
Data from The Flurry Blog, 2013. Available online at http://blog.flurry.com (accessed May 17, 2013).
Data from the United States Department of Agriculture.
Image credit: comedy_nose/flickr
“American Fact Finder.” U.S. Census Bureau. Available online at http://factfinder2.census.gov/faces/nav/jsf/pages/searchresults.xhtml?refresh=t (accessed July 2, 2013).
“Disclosure Data Catalog: Candidate Summary Report 2012.” U.S. Federal Election Commission. Available online at http://www.fec.gov/data/index.jsp (accessed July 2, 2013).
“Headcount Enrollment Trends by Student Demographics Ten-Year Fall Trends to Most Recently Completed Fall.” Foothill De Anza Community College District. Available online at http://research.fhda.edu/factbook/FH_Demo_Trends/FoothillDemographicTrends.htm (accessed September 30,2013).
Kuczmarski, Robert J., Cynthia L. Ogden, Shumei S. Guo, Laurence M. Grummer-Strawn, Katherine M. Flegal, Zuguo Mei, Rong Wei, Lester R. Curtin, Alex F. Roche, Clifford L. Johnson. “2000 CDC Growth Charts for the United States: Methods and Development.” Centers for Disease Control and Prevention. Available online at http://www.cdc.gov/growthcharts/2000growthchart-us.pdf (accessed July 2, 2013).
La, Lynn, Kent German. “Cell Phone Radiation Levels.” c|net part of CBX Interactive Inc. Available online at http://reviews.cnet.com/cell-phone-radiation-levels/ (accessed July 2, 2013).
“Mean Income in the Past 12 Months (in 2011 Inflaction-Adjusted Dollars): 2011 American Community Survey 1-Year Estimates.” American Fact Finder, U.S. Census Bureau. Available online at http://factfinder2.census.gov/faces/tableservices/jsf/pages/productview.xhtml?pid=ACS_11_1YR_S1902&prodType=table (accessed July 2, 2013).
“Metadata Description of Candidate Summary File.” U.S. Federal Election Commission. Available online at http://www.fec.gov/finance/disclosure/metadata/metadataforcandidatesummary.shtml (accessed July 2, 2013).
“National Health and Nutrition Examination Survey.” Centers for Disease Control and Prevention. Available online at http://www.cdc.gov/nchs/nhanes.htm (accessed July 2, 2013).
(Credit: Robert Neff)
Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.
- La, Lynn, and Kent German. "Cell Phone Radiation Levels," CBX Interactive Inc. Available online at http://reviews.cnet.com/cell-phone-radiation-levels (accessed July 2, 2013). ↵
- “2012 College-Bound Seniors Total Group Profile Report,” CollegeBoard, 2012. Available online at http://media.collegeboard.com/digitalServices/pdf/research/TotalGroup-2012.pdf (accessed May 14, 2013). ↵
- Data from The Flurry Blog, 2013. Available online at http://blog.flurry.com (accessed May 17, 2013). ↵
- Data from The Flurry Blog, 2013. Available online at http://blog.flurry.com (accessed May 17, 2013). ↵
- Data from the United States Department of Agriculture. ↵
- “National Health and Nutrition Examination Survey,” Centers for Disease Control and Prevention. Available online at http://www.cdc.gov/nchs/nhanes.htm (accessed May 17, 2013). ↵
- La, Lynn, and Kent German. "Cell Phone Radiation Levels," CBX Interactive Inc. Available online at http://reviews.cnet.com/cell-phone-radiation-levels (accessed July 2, 2013). ↵
- La, Lynn, and Kent German. "Cell Phone Radiation Levels," CBX Interactive Inc. Available online at http://reviews.cnet.com/cell-phone-radiation-levels (accessed July 2, 2013). ↵
- “American Fact Finder,” U.S. Census Bureau. Available online at http://factfinder2.census.gov/faces/nav/jsf/pages/searchresults.xhtml?refresh=t (accessed July 2, 2013). ↵
- “Headcount Enrollment Trends by Student Demographics Ten-Year Fall Trends to Most Recently Completed Fall,” Foothill De Anza Community College District. Available online at http://research.fhda.edu/factbook/FH_Demo_Trends (accessed September 30,2013). ↵
- Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm. ↵
- Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm. ↵
- King, Bill. “Graphically Speaking,” Institutional Research, Lake Tahoe Community College. Available online at http://www.ltcc.edu/web/about/institutional-research (accessed April 3, 2013). ↵

