Chapter 6 Extra Practice
6.1 The Sampling Distribution of the Sample Mean (t)
1. Which two distributions can you use for inference on a mean?
2. Which distribution do you use when you are testing a population mean and the population standard deviation is known and/or n ≥ 30?
3. Which distribution do you use when the standard deviation is not known and you are testing one population mean? Assume sample size is large.
4. A population mean is 13. The sample mean is 12.8, and the sample standard deviation is two. The sample size is 20. What distribution should you use to perform a hypothesis test? Assume the underlying population is normal.
5. A population has a mean is 25 and a standard deviation of five. The sample mean is 24, and the sample size is 108. What distribution should you use to perform a hypothesis test?
6. You are performing a hypothesis test of a single population mean using a Student’s t-distribution. What must you assume about the distribution of the data?
6.2 Inference for the Mean in Practice
1. The Human Toxome Project (HTP) is working to understand the scope of industrial pollution’s effect on the human body. Industrial chemicals may enter the body through pollution or as ingredients in consumer products. In October 2008, the scientists at HTP tested cord blood samples for 20 newborn infants in the United States. The cord blood of the “In utero/newborn” group was tested for 430 industrial compounds, pollutants, and other chemicals, including chemicals linked to brain and nervous system toxicity, immune system toxicity, and reproductive toxicity, in addition to fertility problems. There are health concerns about the effects of some chemicals on the brain and nervous system. The figure below shows how many of the targeted chemicals were found in each infant’s cord blood.[1]
| Number of targeted chemicals | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 79 | 145 | 147 | 160 | 116 | 100 | 159 | 151 | 156 | 126 |
| 137 | 83 | 156 | 94 | 121 | 144 | 123 | 114 | 139 | 99 |
Figure 6.8
Use this sample data to construct a 90% confidence interval for the mean number of targeted industrial chemicals to be found in an infant’s blood.
2. A hospital is trying to cut down on emergency room wait times. It is interested in the amount of time patients must wait before being called back to be examined. An investigation committee randomly surveyed 70 patients. The sample mean was 1.5 hours with a sample standard deviation of 0.5 hours.
- Identify
 ,
, 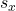 , n, and n – 1.
, n, and n – 1. - Define the random variables X and
 in words.
in words. - Which distribution should you use for this problem?
- Construct a 95% confidence interval for the population mean time spent waiting. State the confidence interval, sketch the graph, and calculate the margin of error.
- Explain in complete sentences what the confidence interval means.
3. One hundred eight Americans were surveyed to determine the number of hours they spend watching television each month. It was revealed that they watched an average of 151 hours each month with a standard deviation of 32 hours. Assume that the underlying population distribution is normal.
- Identify
 ,
, 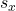 , n, and n – 1.
, n, and n – 1. - Define the random variable X in words.
- Define the random variable
 in words.
in words. - Which distribution should you use for this problem?
- Construct a 99% confidence interval for the population mean hours spent watching television per month. State the confidence interval, sketch the graph, and calculate the margin of error.
- Why would the margin of error change if the confidence level were lowered to 95%?
4. The data in the table below are the result of a random survey of 39 national flags (with replacement between picks) from various countries. We are interested in finding a confidence interval for the true mean number of colors on a national flag. Let X = the number of colors on a national flag.
| X | Frequency |
|---|---|
| 1 | 1 |
| 2 | 7 |
| 3 | 18 |
| 4 | 7 |
| 5 | 6 |
Figure 6.9
- Identify
 ,
, 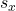 , and n.
, and n. - Define the random variable
 in words.
in words. - What is
 estimating?
estimating? - Is
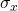 known?
known? - As a result of your answer to the questions above, state the exact distribution to use when calculating the confidence interval.
- Construct a 95% confidence interval for the true mean number of colors on national flags. How much area is in both tails (combined)?
- How much area is in each tail?
- Calculate the lower limit, upper limit, and margin of error.
- The 95% confidence interval is .
- Fill in the blanks on the graph with the areas, the upper and lower limits of the confidence interval, and the sample mean.
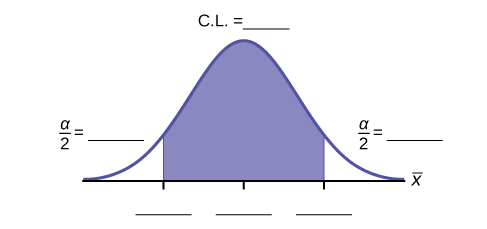
Figure 6.10. Figure description available at the end of the section. - In one complete sentence, explain what the interval means.
- Using the same
 ,
, 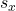 , and level of confidence, suppose that n were 69 instead of 39. Would the margin of error become larger or smaller? How do you know?
, and level of confidence, suppose that n were 69 instead of 39. Would the margin of error become larger or smaller? How do you know? - Using the same
 ,
, 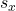 , and n = 39, how would the margin of error change if the confidence level were reduced to 90%? Why?
, and n = 39, how would the margin of error change if the confidence level were reduced to 90%? Why?
5. A random survey of enrollment at 35 community colleges across the United States yielded the following figures: 6,414; 1,550; 2,109; 9,350; 21,828; 4,300; 5,944; 5,722; 2,825; 2,044; 5,481; 5,200; 5,853; 2,750; 10,012; 6,357; 27,000; 9,414; 7,681; 3,200; 17,500; 9,200; 7,380; 18,314; 6,557; 13,713; 17,768; 7,493; 2,771; 2,861; 1,263; 7,285; 28,165; 5,080; 11,622. Assume the underlying population is normal.
- Identify
 ,
, 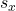 , n, and n – 1.
, n, and n – 1. - Define the random variables
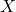 and
and  in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population mean enrollment at community colleges in the United States.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- What would happen to the margin of error and confidence interval if 500 community colleges were surveyed? Why?
6. Suppose that a committee is studying whether or not there is time wasted in our judicial system. It is interested in the mean amount of time individuals waste at the courthouse waiting to be called for jury duty. The committee randomly surveyed 81 people who recently served as jurors. The sample mean wait time was eight hours with a sample standard deviation of four hours.
- Identify
 ,
, 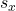 , n, and n – 1.
, n, and n – 1. - Define the random variables
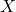 and
and  in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population mean time wasted.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- Explain in a complete sentence what the confidence interval means.
7. A pharmaceutical company makes tranquilizers. It is assumed that the distribution for the length of time they last is approximately normal. Researchers in a hospital used the drug on a random sample of nine patients. The effective period of the tranquilizer for each patient (in hours) was as follows: 2.7, 2.8, 3.0, 2.3, 2.3, 2.2, 2.8, 2.1, and 2.4.
- Identify
 ,
, 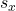 , n, and n – 1.
, n, and n – 1. - Define the random variable
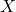 in words.
in words. - Define the random variable
 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population mean length of time.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- What does it mean to be “95% confident” in this problem?
8. Suppose that 14 children who were learning to ride two-wheel bikes were surveyed to determine how long they had to use training wheels. It was revealed that they used them an average of six months with a sample standard deviation of three months. Assume that the underlying population distribution is normal.
- Identify
 ,
, 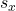 , n, and n – 1.
, n, and n – 1. - Define the random variable
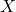 in words.
in words. - Define the random variable
 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 99% confidence interval for the population mean length of time using training wheels.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- Why would the margin of error change if the confidence level were lowered to 90%?
9. Forbes magazine published data on the best small firms in 2012. These were firms that had been publicly traded for at least a year, have a stock price of at least $5 per share, and have reported annual revenue between $5 million and $1 billion. The figure below shows the ages of the corporate CEOs for a random sample of these firms.[2]
| Ages of the corporate CEOs | ||||
|---|---|---|---|---|
| 48 | 58 | 51 | 61 | 56 |
| 59 | 74 | 63 | 53 | 50 |
| 59 | 60 | 60 | 57 | 55 |
| 55 | 63 | 57 | 47 | 55 |
| 57 | 43 | 61 | 62 | 49 |
| 67 | 67 | 55 | 55 | 49 |
Figure 6.11
Use this sample data to construct a 90% confidence interval for the mean age of CEOs for these top small firms. Use the Student’s t-distribution.
10. Unoccupied seats on flights cause airlines to lose revenue. Suppose a large airline wants to estimate its mean number of unoccupied seats per flight over the past year. To accomplish this, the records of 225 flights are randomly selected and the number of unoccupied seats is noted for each of the sampled flights. The sample mean is 11.6 seats, and the sample standard deviation is 4.1 seats.
- Identify
 ,
, 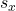 , n, and n – 1.
, n, and n – 1. - Define the random variables
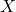 and
and  in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 92% confidence interval for the population mean number of unoccupied seats per flight.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
11. In a recent sample of 84 used car sales costs, the sample mean was $6,425 with a standard deviation of $3,156. Assume the underlying distribution is approximately normal.
- Which distribution should you use for this problem? Explain your choice.
- Define the random variable
 in words.
in words. - Construct a 95% confidence interval for the population mean cost of a used car.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- Explain what a “95% confidence interval” means for this study.
12. Six different national brands of chocolate chip cookies were randomly selected at the supermarket. The grams of fat per serving are 8, 8, 10, 7, 9, and 9. Assume the underlying distribution is approximately normal.
- Construct a 90% confidence interval for the population mean grams of fat per serving of chocolate chip cookies sold in supermarkets.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- If you wanted a smaller margin of error while keeping the same level of confidence, what should have been changed in the study before it was done?
- Go to the store, and record the grams of fat per serving of six brands of chocolate chip cookies.
- Calculate the mean.
- Is the mean within the interval you calculated in (a)? Did you expect it to be? Why or why not?
13. A survey of the mean number of cents saved from coupons was conducted by randomly surveying one coupon per page from the coupon sections of a recent San Jose Mercury News. The following data were collected: 20¢, 75¢, 50¢, 65¢, 30¢, 55¢, 40¢, 40¢, 30¢, 55¢, $1.50, 40¢, 65¢, 40¢.[3] Assume the underlying distribution is approximately normal.
- Identify
 ,
, 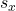 , n, and n – 1.
, n, and n – 1. - Define the random variables
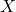 and
and  in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population mean worth of coupons.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- If many random samples were taken of size 14, what percent of the confidence intervals constructed should contain the population mean worth of coupons? Explain why.
14. A quality control specialist for a restaurant chain takes a random sample of size 12 to check the amount of soda served in the 16 oz. serving size. The sample mean is 13.30 with a sample standard deviation of 1.55. Assume the underlying population is normally distributed.
Find the 95% confidence Interval for the true population mean for the amount of soda served.
- Find the 95% confidence Interval for the true population mean for the amount of soda served.
- What is the margin of error?
15. It is believed that Lake Tahoe Community College (LTCC) Intermediate Algebra students get less than seven hours of sleep per night, on average. A survey of 22 LTCC Intermediate Algebra students generated a mean of 7.24 hours with a standard deviation of 1.93 hours. At a level of significance of 5%, do LTCC Intermediate Algebra students get less than seven hours of sleep per night, on average? The distribution to be used for this test is ![]() ~ .
~ .
- N(7.24,
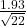 )
) - N(7.24, 1.93)
- t22
- t21
6.3 The Sampling Distribution of the Sample Proportion
1. You are performing a hypothesis test of a single population proportion. What must be true about the quantities of np and nq?
2. You are performing a hypothesis test of a single population proportion. You find out that np is less than five. What must you do to be able to perform a valid hypothesis test?
3. You are performing a hypothesis test of a single population proportion. The data come from which distribution?
6.4 Inference for a Proportion
1. In six packages of The Flintstones® Real Fruit Snacks, there were five Bam-Bam snack pieces. The total number of snack pieces in the six bags was 68. We wish to calculate a 96% confidence interval for the population proportion of Bam-Bam snack pieces.
- Define the random variables X and
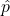 in words.
in words. - Which distribution should you use for this problem? Explain your choice
- Calculate
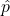 .
. - Construct a 96% confidence interval for the population proportion of Bam-Bam snack pieces per bag.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- Do you think that six packages of fruit snacks yield enough data to give accurate results? Why or why not?
2. For a class project, a political science student at a large university wants to estimate the percent of students who are registered voters. He surveys 500 students and finds that 300 are registered voters. Compute a 90% confidence interval for the true percent of students who are registered voters, and interpret the confidence interval.
3. A student polls his school to see if students in the school district are for or against the new legislation regarding school uniforms. She surveys 600 students and finds that 480 are against the new legislation.
- Compute a 90% confidence interval for the true percent of students who are against the new legislation, and interpret the confidence interval.
- In a sample of 300 students, 68% said they own an iPod and a smartphone. Compute a 97% confidence interval for the true percent of students who own an iPod and a smartphone.
4. Marketing companies are interested in knowing the population percent of women who make the majority of household purchasing decisions.
- When designing a study to determine this population proportion, what is the minimum number you would need to survey to be 90% confident that the population proportion is estimated to within 0.05?
- If it were later determined that it was important to be more than 90% confident and a new survey were commissioned, how would it affect the minimum number you need to survey? Why?
5. Suppose the marketing company randomly surveyed 200 households and found that, in 120 of them, the woman made the majority of the purchasing decisions. We are interested in the population proportion of households where women make the majority of the purchasing decisions.
- Identify x, n, and
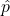 .
. - Define the random variables X and
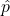 in words.
in words. - Which distribution should you use for this problem?
- Construct a 95% confidence interval for the population proportion of households where the women make the majority of the purchasing decisions. State the confidence interval, sketch the graph, and calculate the margin of error.
- List two difficulties the company might have in obtaining random results if this survey were done by email.
6. Of 1,050 randomly selected adults, 360 identified themselves as manual laborers, 280 identified themselves as non-manual wage earners, 250 identified themselves as mid-level managers, and 160 identified themselves as executives. In the survey, 82% of manual laborers preferred trucks, 62% of non-manual wage earners preferred trucks, 54% of mid-level managers preferred trucks, and 26% of executives preferred trucks.
- We are interested in finding the 95% confidence interval for the percent of executives who prefer trucks. Define random variables X and
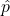 in words.
in words. - Which distribution should you use for this problem?
- Construct a 95% confidence interval. State the confidence interval, sketch the graph, and calculate the margin of error.
- Suppose we want to lower the sampling error. What is one way to accomplish that?
- The sampling error given in the survey is ±2%. Explain what the ±2% means.
7. A poll of 1,200 voters asked what the most significant issue was in the upcoming election. Sixty-five percent answered the economy. We are interested in the population proportion of voters who feel the economy is the most important.
- Define the random variable X in words.
- Define the random variable
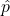 in words.
in words. - Which distribution should you use for this problem?
- Construct a 90% confidence interval, and state the confidence interval and the margin of error.
- What would happen to the confidence interval if the level of confidence were 95%?
8. The Ice Chalet offers dozens of different beginning ice-skating classes. All of the class names are put into a bucket. The 5 PM Monday night beginners class for ages 8 to 12 was picked. In that class, were 64 girls and 16 boys. Suppose that we are interested in the true proportion of girls ages 8 to 12 in all beginners ice-skating classes at the Ice Chalet. Assume that the children in the selected class are a random sample of the population.
- What is being counted?
- In words, define the random variable X.
- Calculate x, n, and
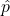 .
. - State the estimated distribution of X. X~ .
- Define a new random variable
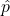 . What is
. What is 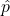 estimating?
estimating? - In words, define the random variable
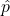 .
. - State the estimated distribution of
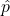 . Construct a 92% confidence interval for the true proportion of girls in the ages 8 to 12 beginners ice-skating classes at the Ice Chalet.
. Construct a 92% confidence interval for the true proportion of girls in the ages 8 to 12 beginners ice-skating classes at the Ice Chalet. - How much area is in both tails (combined)?
- How much area is in each tail?
- Calculate the lower limit, upper limit, and margin of error.
- The 92% confidence interval is .
- Fill in the blanks on the graph with the areas, upper and lower limits of the confidence interval, and the sample proportion.
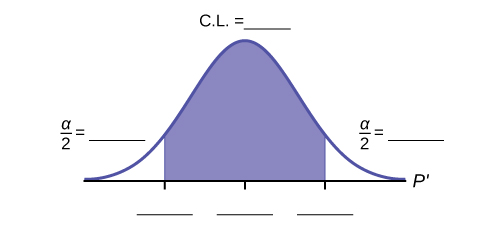
Figure 6.12. Figure description available at the end of the section. - In one complete sentence, explain what the interval means.
- Using the same
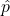 and level of confidence, suppose that n were increased to 100. Would the margin of error become larger or smaller? How do you know?
and level of confidence, suppose that n were increased to 100. Would the margin of error become larger or smaller? How do you know? - Using the same
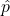 and n = 80, how would the margin of error change if the confidence level were increased to 98%? Why?
and n = 80, how would the margin of error change if the confidence level were increased to 98%? Why? - If you decreased the allowable margin of error, why would the minimum sample size increase (keeping the same level of confidence)?
9. Insurance companies are interested in knowing the population percent of drivers who always buckle up before riding in a car.
- When designing a study to determine this population proportion, what is the minimum number you would need to survey to be 95% confident that the population proportion is estimated to within 0.03?
- If it were later determined that it was important to be more than 95% confident and a new survey was commissioned, how would that affect the minimum number you would need to survey? Why?
Suppose that the insurance companies did do a survey. They randomly surveyed 400 drivers and found that 320 claimed they always buckle up. We are interested in the population proportion of drivers who claim they always buckle up.
- Find x, n, and
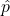 .
. - Define the random variables X and
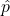 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population proportion who claim they always buckle up.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- If this survey were done by telephone, list three difficulties the companies might have in obtaining random results.
10. According to a survey of 1,200 people, 61% feel that the president is doing an acceptable job. We are interested in the population proportion of people who feel the president is doing an acceptable job.
- Define the random variables X and
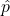 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 90% confidence interval for the population proportion of people who feel the president is doing an acceptable job.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
11. An article regarding interracial dating and marriage appeared in the Washington Post. Of the 1,709 randomly selected adults, 315 identified themselves as Latino/a, 323 identified themselves as Black, 254 identified themselves as Asian, and 779 identified themselves as White. In this survey, 86% of Black people said that they would welcome a White person into their families. Among Asian people, 77% would welcome a White person into their families, 71% would welcome a Latino/a person, and 66% would welcome a Black person.[4]
- We are interested in finding the 95% confidence interval for the percent of all Black adults who would welcome a White person into their families. Define the random variables X and
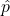 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
12. Refer to the information in Question 11.
- Construct three 95% confidence intervals.
- Percent of all Asian people who would welcome a White person into their families
- Percent of all Asian people who would welcome a Latino/a into their families
- Percent of all Asian people who would welcome a Black person into their families
- Even though the three point estimates are different, do any of the confidence intervals overlap? Which?
- For any intervals that do overlap, in words, what does this imply about the significance of the differences in the true proportions?
- For any intervals that do not overlap, in words, what does this imply about the significance of the differences in the true proportions?
13. Stanford University conducted a study of whether running is healthy for men and women over age 50. During the first eight years of the study, 1.5% of the 451 members of the 50-Plus Fitness Association died. We are interested in the proportion of people over 50 who ran and died in the same eight-year period.
- Define the random variables X and
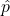 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 97% confidence interval for the population proportion of people over 50 who ran and died in the same eight–year period.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- Explain what a “97% confidence interval” means for this study.
14. A telephone poll of 1,000 adult Americans was reported in an issue of Time Magazine. One of the questions asked was “What is the main problem facing the country?” Twenty percent answered “crime.”[5] We are interested in the population proportion of adult Americans who feel that crime is the main problem.
- Define the random variables X and
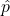 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population proportion of adult Americans who feel that crime is the main problem.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- Suppose we want to lower the sampling error. What is one way to accomplish that?
- The sampling error given by Yankelovich Partners, Inc. (which conducted the poll) is ±3%. In one to three complete sentences, explain what the ±3% represents.
15. Refer to the information above. Another question in the poll was “[How much are] you worried about the quality of education in our schools?” 63% percent responded “a lot.” We are interested in the population proportion of adult Americans who are worried a lot about the quality of education in our schools.
- Define the random variables X and
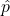 in words.
in words. - Which distribution should you use for this problem? Explain your choice.
- Construct a 95% confidence interval for the population proportion of adult Americans who are worried a lot about the quality of education in our schools.
- State the confidence interval.
- Sketch the graph.
- Calculate the margin of error.
- The sampling error given by Yankelovich Partners, Inc. (which conducted the poll) is ±3%. In one-to-three complete sentences, explain what the ±3% represents.
16. According to a Field Poll, 79% of California adults (400 out of 506 surveyed) feel that “education and our schools” is one of the top issues facing California.[6] We wish to construct a 90% confidence interval for the true proportion of California adults who feel that “education and the schools” is one of the top issues facing California.
- What is a point estimate for the true population proportion?
- A 90% confidence interval for the population proportion is .
- The margin of error is approximately .
17. In a certain Southern California community, 511 homes are randomly surveyed to determine if they meet minimal earthquake preparedness recommendations. Of the homes surveyed, 173 met the minimum recommendations for earthquake preparedness, and 338 did not.
- Find the confidence interval at the 90% confidence level for the true population proportion of Southern California community homes meeting at least the minimum recommendations for earthquake preparedness.
- The point estimate for the population proportion of homes that do not meet the minimum recommendations for earthquake preparedness is .
18. On May 23, 2013, Gallup reported that, of the 1,005 people surveyed, 76% of US workers believe that they will continue working past retirement age. The confidence level for this study was reported at 95% with a ±3% margin of error.[7]
- Determine the estimated proportion from the sample.
- Determine the sample size.
- Identify CL and α.
- Calculate the margin of error based on the information provided.
- Compare the margin of error in (d) to the margin of error reported by Gallup. Explain any differences between the values.
- Create a confidence interval for the results of this study.
- A reporter is covering the release of this study for a local news station. How should she explain the confidence interval to her audience?
19. A national survey of 1,000 adults was conducted on May 13, 2013, by Rasmussen Reports. It concluded with 95% confidence that 49% to 55% of Americans believe that big-time college sports programs corrupt the process of higher education.[8]
- Find the point estimate and the margin of error for this confidence interval.
- Can we (with 95% confidence) conclude that more than half of all American adults believe this?
- Use the point estimate from (a) and n = 1,000 to calculate a 75% confidence interval for the proportion of American adults that believe that major college sports programs corrupt higher education.
- Can we (with 75% confidence) conclude that at least half of all American adults believe this?
20. Public Policy Polling recently conducted a survey asking adults across the US about music preferences. When asked, 80 of the 571 participants admitted that they have illegally downloaded music.[9]
- Create a 99% confidence interval for the true proportion of American adults who have illegally downloaded music.
- This survey was conducted through automated telephone interviews on May 6 and 7, 2013. The margin of error of the survey compensates for sampling error, or natural variability among samples. List some factors that could affect the survey’s outcome that are not covered by the margin of error.
- Without performing any calculations, describe how the confidence interval would change if the confidence level changed from 99% to 90%.
21. You plan to conduct a survey on your college campus to learn about the political awareness of students. You want to estimate the true proportion of college students on your campus who voted in the 2020 presidential election with 95% confidence and a margin of error no greater than 5%. How many students must you interview?
22. In a recent Zogby International Poll, nine of 48 respondents rated the likelihood of a terrorist attack in their community as “likely” or “very likely.”[10] Use the “plus four” method to create a 97% confidence interval for the proportion of American adults who believe that a terrorist attack in their community is likely or very likely. Explain what this confidence interval means in the context of the problem.
6.5 Behavior of Confidence Intervals for a Proportion
1. The Berkman Center for Internet & Society at Harvard recently conducted a study analyzing the privacy management habits of teen internet users.[11] In a group of 50 teens, 13 reported having more than 500 friends on Facebook. Use the “plus four” method to find a 90% confidence interval for the true proportion of teens who would report having more than 500 Facebook friends.
Figure Descriptions
Figure 6.10: This is a template of a normal distribution curve with the central region shaded to represent a confidence interval. The residual areas are on either side of the shaded region. Blanks indicate that students should label the confidence level, residual areas, and points that define the confidence interval.
Figure 6.12: This is a template of a normal distribution curve with the central region shaded to represent a confidence interval. The residual areas are on either side of the shaded region. Blanks indicate that students should label the confidence level, residual areas, and points that define the confidence interval.
References
Figures
Figure 6.10: Figure from Lumen Learning Introduction to Statistics (CC BY 4.0). Retrieved from https://courses.lumenlearning.com/introstats1/chapter/section-exercises-7/
Figure 6.12: Figure from Lumen Learning Introduction to Statistics (CC BY 4.0). Retrieved from https://courses.lumenlearning.com/introstats1/chapter/section-exercises-7/
Text
“America’s Best Small Companies,” Forbes, 2013. Available online at http://www.forbes.com/best-small-companies/list (accessed July 2, 2013).
Data from Microsoft Bookshelf.
Data from Business Week. Available online at http://www.businessweek.com.
Data from Forbes. Available online at http://www.forbes.com.
“Disclosure Data Catalog: Leadership PAC and Sponsors Report, 2012,” Federal Election Commission. Available online at http://www.fec.gov/data/index.jsp (accessed July 2,2013).
“Human Toxome Project: Mapping the Pollution in People,” Environmental Working Group. Available online at http://www.ewg.org/sites/humantoxome/participants/participant-group.php?group=in+utero%2Fnewborn (accessed July 2, 2013).
“Metadata Description of Leadership PAC List,” Federal Election Commission. Available online at http://www.fec.gov/finance/disclosure/metadata/metadataLeadershipPacList.shtml (accessed July 2, 2013).
Jensen, Tom. “Democrats, Republicans Divided on Opinion of Music Icons,” Public Policy Polling. Available online at http://www.publicpolicypolling.com/Day2MusicPoll.pdf (accessed July 2, 2013).
Madden, Mary, Amanda Lenhart, Sandra Coresi, Urs Gasser, Maeve Duggan, Aaron Smith, and Meredith Beaton. “Teens, Social Media, and Privacy,” PewInternet, 2013. Available online at http://www.pewinternet.org/Reports/2013/Teens-Social-Media-And-Privacy.aspx (accessed July 2, 2013).
Prince Survey Research Associates International. “2013 Teen and Privacy Management Survey,” Pew Research Center: Internet and American Life Project. Available online at http://www.pewinternet.org/~/media//Files/Questionnaire/2013/Methods%20and%20Questions_Teens%20and%20Social%20Media.pdf (accessed July 2, 2013).
Saad, Lydia. “Three in Four U.S. Workers Plan to Work Past Retirement Age: Slightly more say they will do this by choice rather than necessity,” Gallup Economy, 2013. Available online at http://www.gallup.com/poll/162758/three-four-workers-plan-work-past-retirement-age.aspx (accessed July 2, 2013).
The Field Poll. Available online at http://7eld.com/7eldpollonline/subscribers/ (accessed July 2, 2013).
“New SUNYIT/Zogby Analytics Poll: Few Americans Worry about Emergency Situations Occurring in Their Community; Only one in three have an Emergency Plan; 70% Support Infrastructure ‘Investment’ for National Security,” Zogby Analytics, 2013. Available online at http://www.zogbyanalytics.com/news/299-americans-neither-worried-nor-prepared-in-case-of-a-disaster-sunyit-zogby-analytics-poll (accessed July 2, 2013).
“52% Say Big-Time College Athletics Corrupt Education Process,” Rasmussen Reports, 2013. Available online at http://www.rasmussenreports.com/public_content/lifestyle/sports/may_2013/52_say_big_time_college_athletics_corrupt_education_process (accessed July 2, 2013).
- “Human Toxome Project: Mapping the Pollution in People,” Environmental Working Group. Available online at http://www.ewg.org/sites/humantoxome/participants/participant-group.php?group=in+utero%2Fnewborn (accessed July 2, 2013). ↵
- “America’s Best Small Companies.” Forbes, 2013. Available online at http://www.forbes.com/best-small-companies/list/ (accessed July 2, 2013). ↵
- Data from San Jose Mercury News ↵
- Fears, Darryl, and Claudia Deane. "Biracial Couples Report Tolerance," Washington Post, July 5, 2001. Available online at https://www.washingtonpost.com/archive/politics/2001/07/05/biracial-couples-report-tolerance/c1ce88c8-ba7c-44f5-a348-b86776df9112 (accessed January 26, 2021). ↵
- Data from Time Magazine; survey by Yankelovich Partners, Inc. ↵
- The Field Poll. Available online at http://field.com/fieldpollonline/subscribers/ (accessed July 2, 2013). ↵
- Saad, Lydia. “Three in Four U.S. Workers Plan to Work Pas Retirement Age: Slightly more say they will do this by choice rather than necessity,” Gallup Economy, 2013. Available online at http://www.gallup.com/poll/162758/three-fourworkers-plan-work-past-retirement-age.aspx (accessed July 2, 2013). ↵
- “52% Say Big-Time College Athletics Corrupt Education Process,” Rasmussen Reports, 2013. Available online at http://www.rasmussenreports.com/public_content/lifestyle/sports/may_2013/52_say_big_time_college_athletics_corrupt_education_process (accessed July 2, 2013). ↵
- Jensen, Tom. “Democrats, Republicans Divided on Opinion of Music Icons,” Public Policy Polling. Available online at http://www.publicpolicypolling.com/Day2MusicPoll.pdf (accessed July 2, 2013). ↵
- “New SUNYIT/Zogby Analytics Poll: Few Americans Worry about Emergency Situations Occurring in Their Community; Only one in three have an Emergency Plan; 70% Support Infrastructure ‘Investment’ for National Security,” Zogby Analytics, 2013. Available online at http://www.zogbyanalytics.com/news/299-americans-neither-worried-norprepared-in-case-of-a-disaster-sunyit-zogby-analytics-poll (accessed July 2, 2013). ↵
- Prince Survey Research Associates International. “2013 Teen and Privacy Management Survey,” Pew Research Center: Internet and American Life Project. Available online at http://www.pewinternet.org/~/media//Files/Questionnaire/2013/Methods%20and%20Questions_Teens%20and%20Social%20Media.pdf (accessed July 2, 2013). ↵

