3.3 Measures of Association
You can look at the scatter plot and see that a linear relationship seems reasonable, and you can identify a positive or negative trend, but how can you tell more about this relationship? While it is always good practice to first examine things visually, you may find that deciphering a scatter plot can be tricky, especially when it comes to the strength of a relationship. The next step is then to calculate numerical measures of this association.
The Correlation Coefficient, r
The correlation coefficient, r, developed by Karl Pearson in the early 1900s, is a numerical measure of the strength and direction of the linear association between the independent variable x and the dependent variable y.
The correlation coefficient can be calculated using the formula:
![r=\frac{n\Sigma \left(xy\right)-\left(\Sigma x\right)\left(\Sigma y\right)}{\sqrt{\left[n\Sigma {x}^{2}-{\left(\Sigma x\right)}^{2}\right]\left[n\Sigma {y}^{2}-{\left(\Sigma y\right)}^{2}\right]}}](https://pressbooks.lib.vt.edu/app/uploads/quicklatex/quicklatex.com-8aca5abc02f2171e49f01320065c7e4c_l3.png "Rendered by QuickLaTeX.com")
where n = the number of data points.
The formula for r is formidable, so I would not recommend doing this by hand, but technology can make quick work of the calculation.
If you suspect a linear relationship between x and y, then r can measure the strength of the linear relationship.
What the VALUE of r tells us:
- The value of r is always between –1 and +1 (i.e., –1 ≤ r ≤ 1).
- The size of the correlation r indicates the strength of the linear relationship between x and y. Values of r close to –1 or to +1 indicate a stronger linear relationship between x and y.
- If r = 0, there is likely no linear correlation. It is important to view the scatter plot, however, because data exhibiting a curved or horizontal pattern may have a correlation of 0.
- If r = 1, there is perfect positive correlation. If r = –1, there is perfect negative correlation. In both these cases, all of the original data points lie on a straight line. Of course, in the real world, this will not generally happen.
What the SIGN of r tells us:
- A positive value of r means that when x increases, y tends to increase, and when x decreases, y tends to decrease (positive correlation).
- A negative value of r means that when x increases, y tends to decrease, and when x decreases, y tends to increase (negative correlation).
- The sign of r is the same as the sign of the slope of the best-fit line (b).
NOTE:
Strong correlation does not suggest that x causes y or y causes x. We say “correlation does not imply causation.”
Example
A random sample of 11 statistics students produced the following data, where x is the third exam score out of 80, and y is the final exam score out of 200.
Third exam score 
|
Final exam score 
|
|---|---|
| 65 | 175 |
| 67 | 133 |
| 71 | 185 |
| 71 | 163 |
| 66 | 126 |
| 75 | 198 |
| 67 | 153 |
| 70 | 163 |
| 71 | 159 |
| 69 | 151 |
| 69 | 159 |
Figure 3.13: Third and final exam scores data
A scatter plot showing the scores on the final exam based on scores from the third exam is shown below.
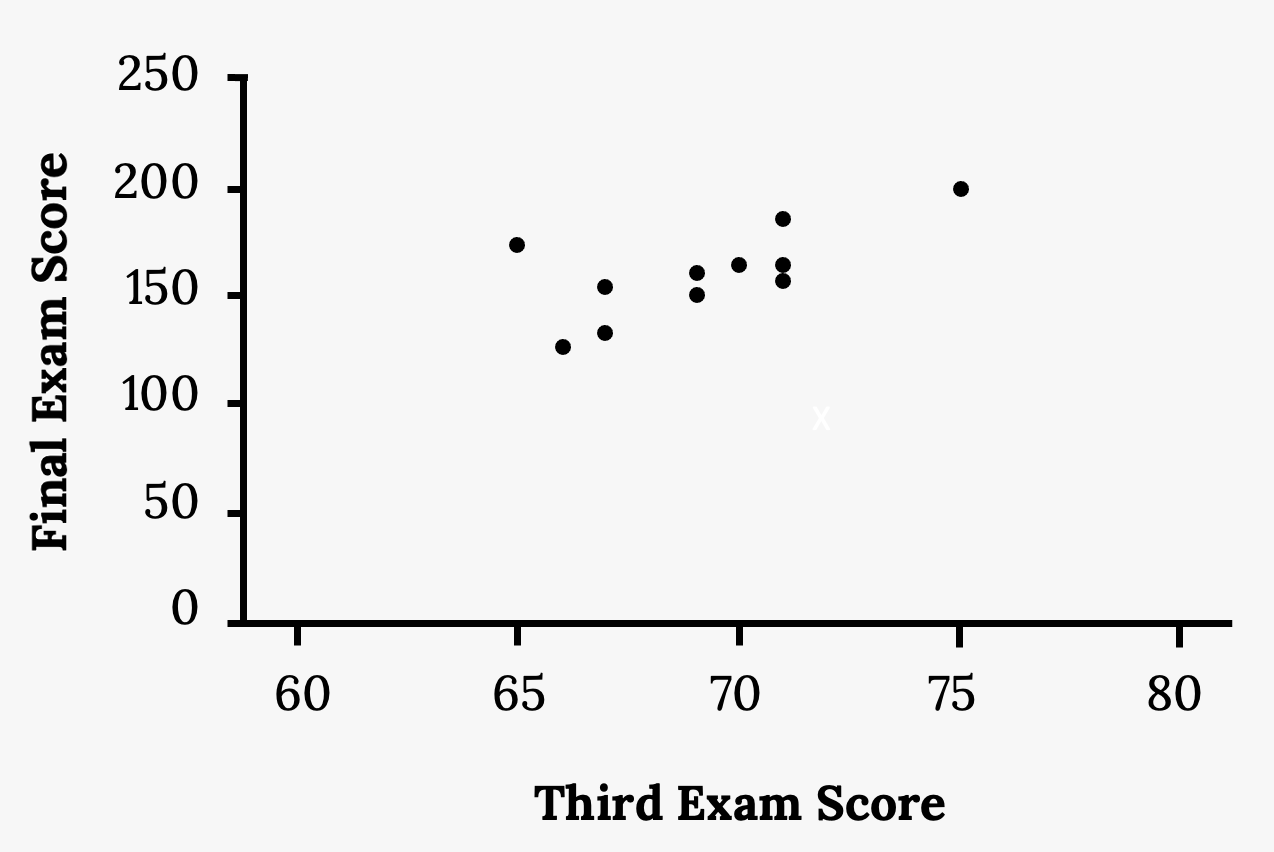
Find the correlation coefficient.
Solution
Using technology we would find the correlation coefficient is r = 0.6631.
Your Turn!
Match the following scatter plots with the three descriptions of correlation coefficients below them.
- –1 < r < 0
- r = 0
- 0 < r < 1
Solution
(a) 0 < r < 1, (b) –1 < r < 0, (c) r = 0
The Coefficient of Determination, r2
While the coefficient of determination (r2) is (obviously) the square of the correlation coefficient, it is usually stated as a percent rather than in decimal form. It has an interpretation in the context of the data:
- r2, when expressed as a percent, represents the percent of variation in the dependent (predicted) variable y that can be explained by variation in the independent (explanatory) variable x using the regression (best-fit) line.
- 1 – r2, when expressed as a percentage, represents the percent of variation in y that is NOT explained by variation in x using the regression line. This can be seen as the scattering of the observed data points about the regression line.
Example
Recall our previous example using a student’s third exam scores to predict their final exam scores, in which the correlation coefficient is r = 0.6631.
Find the coefficient of determination.
Solution
r2 = 0.663122 = 0.4397
Interpret of r2 in the context of this example.
Solution
Approximately 44% of the variation (0.4397 is approximately 0.44) in the final-exam grades can be explained by the variation in the grades on the third exam, using the best-fit regression line.
Therefore, approximately 56% of the variation (1 – 0.44 = 0.56) in the final exam grades can NOT be explained by the variation in the grades on the third exam, using the best-fit regression line. (This is seen as the scattering of the points about the line.)
Figure References
Figure 3.14: Kindred Grey (2020). Third and final exam scores scatter plot. CC BY-SA 4.0. Adaptation of Figure 12.9 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/12-3-the-regression-equation
Figure 3.15: Kindred Grey (2020). Matching scatter plots to correlation coefficients. CC BY-SA 4.0. Adaptation of Figure 12.13 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/12-3-the-regression-equation
A numerical measure that provides a measure of strength and direction of the linear association between the independent variable x and the dependent variable y
A numerical measure of the percentage or proportion of variation in the dependent variable (y) that can be explained by the independent variable (x)
