Statistical Inference

It is often necessary to guess, infer, or generalize about the outcome of an event in order to make a decision. Politicians study polls to guess their likelihood of winning an election. Teachers choose a particular course of study based on what they think students can comprehend. Doctors choose the treatments needed for various diseases based on their assessment of likely results. You may have visited a casino where people choose games based on their perceived likelihood of winning. You may have chosen your course of study based on the probable availability of jobs.

Statistical inference uses what we know about probability to make our best guesses, or estimates, from samples about the population from which they came. The main forms of inference are:

1. Point estimation
2. Confidence interval
3. Hypothesis testing

Point Estimation

Suppose you are trying to determine the mean rent of a two-bedroom apartment in your town. You might look in the classified section of the newspaper, write down several rents listed, and average them together. You would have obtained a point estimate of the true mean. If you are trying to determine the percentage of times you make a basket when shooting a basketball, you might count the number of shots you make and divide that by the number of shots you attempt. In this case, you would have obtained a point estimate for the true proportion.

The most natural way to estimate features of the population (parameters) is to use the corresponding summary statistic calculated from the sample. Some common point estimates and their corresponding parameters are found in the following table:

Parameter	Measure	Statistic
	Mean of a single population
	Proportion of a single population
	Mean difference of two dependent populations (matched pairs)
	Difference in means of two independent populations
	Difference in proportions of two populations
	Variance of a single population
	Standard deviation of a single population

Figure 5.2: Parameters and point estimates

Suppose the mean weight of a sample of 60 adults is 173.3 lbs; this sample mean is a point estimate of the population mean weight, µ. Remember this is one of many samples that we could have taken from the population. If a different random sample of 60 individuals was taken from the same population, the new sample mean would likely be different as a result of sampling variability. While estimates generally vary from one sample to another, the population mean is a fixed value.

Suppose a poll suggested the US President’s approval rating is 45%. We would consider 45% to be a point estimate of the approval rating we might see if we collected responses from the entire population. This entire-population response proportion is generally referred to as the parameter of interest. When the parameter is a proportion, it is often denoted by p, and we often refer to the sample proportion as (pronounced “p-hat”). Unless we collect responses from every individual in the population, p remains unknown, and we use as our estimate of p.

How would one estimate the difference in average weight between men and women? Suppose a sample of men yields a mean of 185.1 lbs, and a sample of women men yields a mean of 162.3 lbs. What is a good point estimate for the difference in these two population means? We will expand on this in following chapters.

Sampling Distributions

We have established that different samples yield different statistics due to sampling variability. These statistics have their own distributions, called sampling distributions, that reflect this as a random variable. The sampling distribution of a sample statistic is the distribution of the point estimates based on samples of a fixed size, n, from a certain population. It is useful to think of a particular point estimate as being drawn from a sampling distribution.

Recall the sample mean weight calculated from a previous sample of 173.3 lbs. Suppose another random sample of 60 participants might produce a different value of x, such as 169.5 lbs. Repeated random sampling could result in additional different values, perhaps 172.1 lbs, 168.5 lbs, and so on. Each sample mean can be thought of as a single observation from a random variable X. The distribution of X is called the sampling distribution of the sample mean, and it has its own mean and standard deviation like the random variables discussed previously. We will simulate the concept of a sampling distribution using technology to repeatedly sample, calculate statistics, and graph them. However, the actual sampling distribution would only be attainable if we could theoretically take an infinite amount of samples.

Each of the point estimates in the table above have their own unique sampling distributions that we will explore in the future.

Unbiased Estimation

Although variability in samples is present, there remains a fixed value for any population parameter. What makes a statistical estimate of this parameter of interest “good”? It must be both accurate and precise.

The accuracy of an estimate refers to how well it estimates the actual value of that parameter. Mathematically, this is true when the expected value of your statistic is equal to the value of that parameter. Visually, this looks like the center of the sampling distribution being situated at the value of that parameter.

According to the law of large numbers, probabilities converge to what we expect over time. Point estimates follow this rule, becoming more accurate with increasing sample size. The figure below shows the sample mean weight calculated for random samples drawn, where sample size increases by one for each draw until sample size equals 500. The maroon dashed horizontal line is drawn at the average weight of all adults (169.7 lbs), which represents the population mean weight according to the CDC.

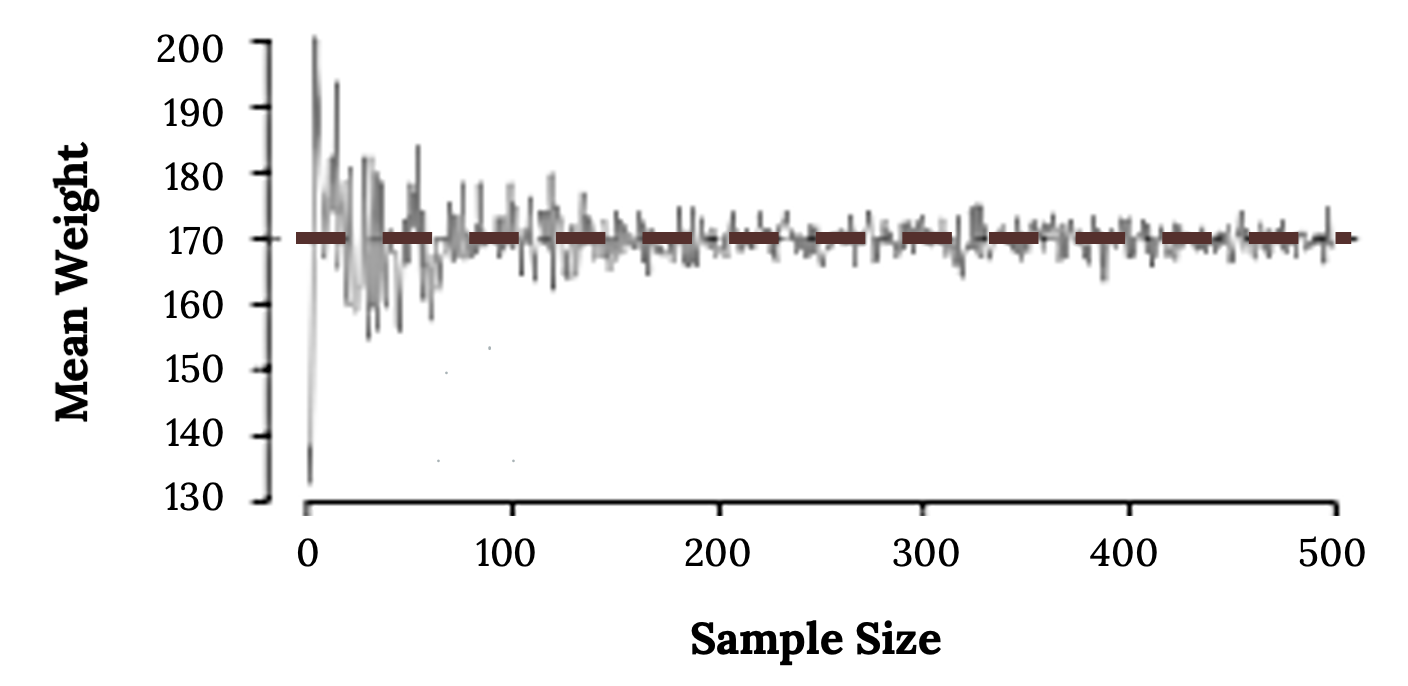
Note how a sample size around 50 may produce a sample mean that is as much as 10 lbs higher or lower than the population mean. As sample size increases, the fluctuations around the population mean decrease; in other words, as sample size increases, the sample mean becomes less variable and provides a more reliable estimate of the population mean.

In addition to accuracy, a precise estimate is also more useful. This means that the values of the statistics seem pretty close together over repeated sampling. The precision of an estimate can be visualized as the spread of the sampling distribution, usually quantified by the standard deviation. The standard deviation of a sampling distribution is often referred to as the standard error. Smaller standard errors are affected by sample size and lead to more precise estimates.

Figure References

Figure 5.1: Matthew Lancaster (2020). Silver round coins on clear glass jar. Unsplash license. https://unsplash.com/photos/silver-round-coins-on-clear-glass-jar-ip1eu-cw49A

Figure 5.3: Kindred Grey (2020). Law of large numbers. CC BY-SA 4.0.

Figure Descriptions

Figure 5.1: A glass jar of coins sits on a dark wooden table.

Figure 5.3: Line graph with sample size on the x axis and mean weight on the y axis. When sample size is small (x=10) the mean weight varies. As sample size increases (x=500) the mean weight does not vary as much. Overall graph mimics a cornucopia shape with the wide side on the left and narrow side on the right.