2.7 Measures of Spread

Adapted by John Morgan Russell; from Barbara Illowsky and Susan Dean, David Diez, Mine Cetinkaya-Rundel and Christopher D. Barr; Julie Vu and David Harrington

2.7 Measures of Spread

We have made it to spread, the final key aspect of the acronym SOCS.

Shape
Outliers
Center
Spread

A complement to the center of a distribution is the data’s spread (also known as variation or variability). In some datasets, the values are concentrated closely, while they are more spread out in others. Some rough measures of spread we have already discussed are the range and IQR. The most common measure of spread is the standard deviation.

Similar to measures of center, the shape of the distribution and the presence of extreme values can dictate what measure of spread is most appropriate to describe the distribution.

The Interquartile Range

Recall the interquartile range (IQR):

IQR = Q₃ – Q₁.

In addition to helping us establish our fences and identify outliers, the IQR indicates the spread of the middle half (middle 50%) of the data. The IQR can be used as a somewhat rough but very robust measure of spread when outliers may be present. It is often used alongside the median to describe the center and spread of skewed distributions.

Simply showing the five-number summary or a box plot can be a good way to get all of the information for a skewed dataset in one place.

The Standard Deviation

The standard deviation is a measure of spread that assesses how dispersed values are from their mean. It is essentially the “average” deviation—the distance of each observation from the mean.

Not only does it provide a numerical measure of the overall amount of variation in a dataset, it can also be used for other purposes.

The lowercase letter s represents the sample standard deviation, and the lowercase Greek letter σ (sigma) represents the population standard deviation.

By extension, s² represents the sample variance, and the lowercase Greek letter σ² represents the population variance.

The standard deviation is small when the data are all concentrated close to the mean, exhibiting little variation or spread. The standard deviation is larger when the data values are more spread out from the mean, exhibiting more variation. It must always greater than or equal to zero.

Suppose that we are studying the amount of time customers wait in line at the checkout at Supermarket A and Supermarket B. The average wait time at both supermarkets is five minutes. At Supermarket A, the standard deviation for the wait time is two minutes; at Supermarket B, the standard deviation for the wait time is four minutes.

Because Supermarket B has a higher standard deviation, we know that there is more variation in the wait times at supermarket B. Overall, wait times at Supermarket B are more spread out from the average; wait times at Supermarket A are more concentrated near the average.

Calculating the Standard Deviation

The procedure to calculate the standard deviation can be tedious and depends on whether the data are from the entire population or a sample. The calculations are similar but not identical.

If x is a number, then the difference “x – mean” is its deviation. In a dataset, there are as many deviations as there are items in the set. The deviations can show how spread out the data are from the mean. A positive deviation occurs when the data value is greater than the mean, whereas a negative deviation occurs when the data value is less than the mean. If the numbers belong to a population, a deviation is x – μ in symbols. For sample data, a deviation is x – $\overline{x}$ in symbols. If you add the deviations, the sum is always zero, so you cannot simply add the deviations to get the spread of the data. You can fix this by squaring the deviations, making them positive numbers; therefore, the sum will also be positive.

The variance is the average of the squares of the deviations (the x – $\overline{x}$ values for a sample or the x – μ values for a population). The variance, then, is the average squared deviation, which we use to get the standard deviation. The symbol σ² represents the population variance; the population standard deviation σ is the square root of the population variance. The symbol s² represents the sample variance; the sample standard deviation s is the square root of the sample variance. You can think of the standard deviation as a special average of the deviations.

If the numbers come from a census of the entire population and not a sample, when we calculate the average of the squared deviations to find the variance, we divide by N, the number of items in the population. If the data are from a sample rather than a population, when we calculate the average of the squared deviations, we divide by n – 1, one less than the number of items in the sample. Why not divide by n for a sample? The answer has to do with the population variance. The sample variance is an estimate of the population variance. Based on the theoretical mathematics underlying these calculations, dividing by n – 1 gives a better estimate of the population variance.

Formulas

The sample standard deviation

$s=\sqrt{\frac{\Sigma {\left(x-\overline{x}\right)}^{2}}{n-1}}$

The population standard deviation

$\sigma = \sqrt{\frac{\Sigma {\left(x-\mu \right)}^{2}}{N}}$

NOTES:

The variance, whether population (σ²) or sample (s²), can be obtained if you do not apply the square root in their respective formulas
Though we typically rely on technology to calculate the standard deviation in practice, please note:
- In the sample standard deviation formula, the denominator is n – 1.
- In the population standard deviation formula, the denominator is N.
- You may need to indicate on your technology of choice which form of the formula you want to use.
We will often use the sample standard deviation or variance to estimate the population standard deviation or variance.

Example

The teacher of a fifth grade class was interested in the average age and the sample standard deviation of the ages of her students. The following data are the ages for a sample of n = 20 fifth grade students. The ages are rounded to the nearest half year: 9, 9.5, 9.5, 10, 10, 10, 10, 10.5, 10.5, 10.5, 10.5, 11, 11, 11, 11, 11, 11, 11.5, 11.5, 11.5.

First, try to find the mean and standard deviation by hand. Here is a table with the intermediate steps:

X	Deviations	Deviations²
9	9 – 10.525 = –1.525	(–1.525)² = 2.325625
9.5	9.5 – 10.525 = –1.025	(–1.025)² = 1.050625
9.5	9.5 – 10.525 = –1.025	(–1.025)² = 1.050625
10	10 – 10.525 = –0.525	(–0.525)² = 0.275625
10	10 – 10.525 = –0.525	(–0.525)² = 0.275625
10	10 – 10.525 = –0.525	(–0.525)² = 0.275625
10	10 – 10.525 = –0.525	(–0.525)² = 0.275625
10.5	10.5 – 10.525 = –0.025	(–0.025)² = 0.000625
10.5	10.5 – 10.525 = –0.025	(–0.025)² = 0.000625
10.5	10.5 – 10.525 = –0.025	(–0.025)² = 0.000625
10.5	10.5 – 10.525 = –0.025	(–0.025)² = 0.000625
11	11 – 10.525 = 0.475	(0.475)² = 0.225625
11	11 – 10.525 = 0.475	(0.475)² = 0.225625
11	11 – 10.525 = 0.475	(0.475)² = 0.225625
11	11 – 10.525 = 0.475	(0.475)² = 0.225625
11	11 – 10.525 = 0.475	(0.475)² = 0.225625
11	11 – 10.525 = 0.475	(0.475)² = 0.225625
11.5	11.5 – 10.525 = 0.975	(0.975)² = 0.950625
11.5	11.5 – 10.525 = 0.975	(0.975)² = 0.950625
11.5	11.5 – 10.525 = 0.975	(0.975)² = 0.950625
-	-	Total = 9.7375

Figure 2.54: Fifth grade ages

Verify your answers with your choice of technology.

Solution

Mean = $\bar{x}$ = $\frac{9+9.5+9.5+10+10+10+10+10.5+10.5+10.5+10.5+11+11+11+11+11+11+11.5+11.5+11.5}{20}$ = $\frac{210.5}{20}$ = 10.525

The variance may be calculated by hand according to the table above.

The sample variance, s², is equal to the sum of the last column (9.7375) divided by the total number of data values minus one (20 – 1):

s² = $\frac{9.7375}{20-1}$ = 0.5125. Notice that instead of dividing by n = 20, the calculation divided by n – 1 = 20 – 1 = 19 because the data is a sample.

The sample standard deviation, s, is equal to the square root of the sample variance:

s = $\sqrt{0.5125}$ = 0.715891 which is rounded to two decimal places, s = 0.72.

Your Turn!

On a baseball team, the ages of each of the players are as follows:

21, 21, 22, 23, 24, 24, 25, 25, 28, 29, 29, 31, 32, 33, 33, 34, 35, 36, 36, 36, 36, 38, 38, 38, 40

First, try to find the mean and standard deviation by hand. If you get stuck or want to check your work, plug it into your calculator or use your computer software.

The standard deviation, s or σ, is either zero or larger than zero. Describing the data with reference to the spread is called “variability.” The variability in data depends upon the method by which the outcomes are obtained (e.g., by measuring or random sampling). When the standard deviation is zero, there is no spread; all the data values are equal to each other. The standard deviation is small when the data are all concentrated close to the mean, and it is larger when the data values show more variation from the mean. When the standard deviation is a lot larger than zero, the data values are very spread out from the mean; outliers can make s or σ very large.

The Standard Deviation in Context

When first presented, the standard deviation can seem unclear. By graphing your data, you can get a better “feel” for the deviations and the standard deviation. You will find that the standard deviation can be very helpful in symmetrical distributions, but in skewed distributions, the standard deviation may not be much help. The reason is that the two sides of a skewed distribution have different spreads. In a skewed distribution, it is better to look at the first quartile, the median, the third quartile, the smallest value, and the largest value. Because numbers can be confusing, always graph your data, displaying it in a histogram or a box plot.

A number line may also help you understand standard deviation. If we were to put 5 and 7 on a number line, 7 is to the right of 5. We say, then, that 7 is one standard deviation to the right of 5 because 5 + (1)(2) = 7.

If one were also part of the dataset, then 1 is two standard deviations to the left of 5 because 5 + (–2)(2) = 1.

Blank number line in intervals of 1 from 0 to 7. — Figure 2.55: Number line. Figure description available at the end of the section.

In general, a value = mean + (#ofSTDEV)(standard deviation)
where #ofSTDEVs = the number of standard deviations
#ofSTDEV does not need to be an integer.
1 is two standard deviations less than the mean of 5 because 1 = 5 + (–2)(2).

The equation value = mean + (#ofSTDEVs)(standard deviation) can be expressed for a sample and for a population.

Sample:

x = $\overline{x}$ + (#ofSTDEVs)(s)

Population:

x = μ + (#ofSTDEVs)(σ)

Example

Suppose that Rosa and Binh both shop at Supermarket A. Rosa waits at the checkout counter for seven minutes, and Binh waits for one minute. At Supermarket A, the mean waiting time is five minutes, and the standard deviation is two minutes. The standard deviation can be used to determine whether a data value is close to or far from the mean.

Rosa waits for seven minutes:

Seven is two minutes longer than the average of five; two minutes is equal to one standard deviation.
Rosa’s wait time of seven minutes is two minutes longer than the average of five minutes.
Rosa’s wait time of seven minutes is one standard deviation above the average of five minutes.

Binh waits for one minute:

One is four minutes less than the average of five; four minutes is equal to two standard deviations.
Binh’s wait time of one minute is four minutes less than the average of five minutes.
Binh’s wait time of one minute is two standard deviations below the average of five minutes.

Your Turn!

Recall the previous example about the age of fifth grade students where $\overline{x}$ = 10.525 and s² = 0.7159.

Find the value that is one standard deviation above the mean. Find ( $\overline{x}$ + 1s).

Solution

$\overline{x}$ + 1s = 10.53 + (1)(0.72) = 11.25

Find the value that is two standard deviations below the mean. Find ( $\overline{x}$ – 2s).

Solution

$\overline{x}$ – 2s = 10.53 – (2)(0.72) = 9.09

Find the values that are 1.5 standard deviations from (below and above) the mean.

Solution

$\overline{x}$ – 1.5s = 10.53 – (1.5)(0.72) = 9.45

$\overline{x}$ + 1.5s = 10.53 + (1.5)(0.72) = 11.61

z-Scores

The standard deviation can also be used to calculate a measure of location called a z-score. It represents the number of standard deviations between a given observation and its mean (#ofSTDEVs above), which is often denoted with just the letter z. In symbols, the formulas become:

z-Score formulas
Sample	$x = \overline{x} + zs$	$z = \frac{x - \overline{x}}{s}$
Population	$x = \mu + z\sigma$	$z = \frac{x - \mu}{\sigma}$

Figure 2.56: z-Score formulas

Not only are z-scores a useful measure of location for specific observations, they can also be used for other purposes. If two datasets have different means and standard deviations, then comparing the data values directly can be misleading. However, using z-scores, it is possible to put things on a level playing field to compare them.

For each data value, calculate the number of standard deviations between the value and its mean.
Use the formula: value = mean + (#ofSTDEVs)(standard deviation); solve for #ofSTDEVs.
#ofSTDEVs = $\frac{value-mean}{standard \: deviation}$
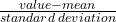
Compare the results of this calculation.

To understand the concept, suppose X ~ N(5, 6) represents weight gains for one group of people who are trying to gain weight in a six-week period, and Y ~ N(2, 1) measures the same weight gain for a second group of people. A negative weight gain would be a weight loss. Since x = 17 and y = 4 are each two standard deviations to the right of their means, they represent the same, standardized weight gain relative to their means.

Example

John and Ali, two students from different high schools, wanted to find out who had the highest GPA when compared to the rest of his school. Which student had the highest GPA when compared to his school?

Student	GPA	School mean GPA	School standard deviation
John	2.85	3.0	0.7
Ali	77	80	10

Figure 2.57: GPA comparisons

For each student, determine how many standard deviations (#ofSTDEVs) his GPA is away from the average for his school. Pay careful attention to signs when comparing and interpreting the answer.

z = #ofSTDEVs = $\frac{value-mean}{standard \: deviation}$ = $\frac{x-\mu}{\sigma}$

Solution

For John, z = #ofSTDEVs = $\frac{2.85-3}{0.7}$ = -0.21

For Ali, z = #ofSTDEVs = $\frac{77-80}{10}$ = -0.3

John has the better GPA when compared to his school because his GPA is 0.21 standard deviations below his school’s mean while Ali’s GPA is 0.3 standard deviations below her school’s mean.

John’s z-score of –0.21 is higher than Ali’s z-score of –0.3. For GPA, higher values are better, so we conclude that John has the better GPA when compared to his school.

Your Turn!

Angie and Beth, two swimmers from different teams, wanted to find out who had the fastest time for the 50 meter freestyle when compared to the rest of her team. Which swimmer had the fastest time when compared to her team?

Swimmer	Time (seconds)	Team mean time	Team standard deviation
Angie	26.2	27.2	0.8
Beth	27.3	30.1	1.4

Figure 2.58: Swim time comparisons

Identifying “Unusual” Observations

Recall we have already established our fence rules for numerically identifying outliers in any distribution. However, for most symmetric and bell-shaped distributions, anything outside of two standard deviations (a z-score below -2 or greater than 2) is considered “unusual”. We will learn more about this in later chapters, but generally an observation should be within ±2 standard deviations 95% of the time. However, considering data to be far from the mean if it is more than two standard deviations away is more of an approximate “rule of thumb” than a rigid rule.

Example

The distribution of heights for US males is considered to be symmetric and bell-shaped, with an average of 69.7 inches and a 2.8 inch standard deviation. How tall would a male have to be to be considered “unusually” tall in the US?

Solution

69.7 + (2*2.8) = 75.3 inches

Your Turn!

The distribution of heights for US females is considered to be symmetric and bell-shaped, with an average of 64.4 and a 2.4 inch standard deviation. How short would a female have to be to be considered “unusually” short in the US?

Additional Resources

QR code

Click here for additional multimedia resources, including podcasts, videos, lecture notes, and worked examples.

If you are using an offline version of this text, access the resources for this section via the QR code, or by visiting https://doi.org/10.7294/26207456.

Figure References

Figure 2.55: Kindred Grey (2020). Number line. CC BY-NC 4.0.

Figure Descriptions

Figure 2.55: Blank number line in intervals of 1 from 0 to 7.

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Significant Statistics: An Introduction to Statistics Copyright © 2024 by John Morgan Russell is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

The Interquartile Range

The Standard Deviation

Calculating the Standard Deviation

Formulas

The Standard Deviation in Context

Identifying “Unusual” Observations

License

Share This Book