Let’s keep working through the acronym SOCS for describing key aspects of our data, this time focusing on outliers.

• Shape
• Outliers
• Center
• Spread

Measures of location are used to quantify where an observation stands in relation to the rest of the distribution. They also provide the building blocks to formally identify outliers. Common measures of location are quartiles and percentiles. Quartiles divide ordered data into quarters, while percentiles divide ordered data into hundredths.

Percentiles

Percentiles are useful for comparing values. For this reason, universities and colleges use percentiles extensively, such as when they use SAT results to determine a minimum test score that will be an acceptance factor. For example, suppose Duke accepts SAT scores at or above the 75th percentile. That translates into a score of at least 1220.

To score in the 90th percentile of an exam does not necessarily mean that you received 90% on a test. It means that 90% of test scores are the same or less than your score and that 10% of test scores are the same or greater than your test score.

Percentiles are mostly used with very large populations. Therefore, it would be acceptable to say that 90% of the test scores are less (and not the same or less) than your score, because removing one particular data value is not significant.

There are two inverse ways you may work with percentiles: finding the kth percentile of a distribution or finding the percentile of a given observation.

Finding the kth Percentile of a Distribution

Sometimes you may want to find the “kth” percentile of a distribution. For instance, what would a student have to score on the SAT to be in the 90th percentile?

If you were to do a little research, you would find several processes for calculating the kth percentile. Here is one of them.

k = the kth percentile. It may or may not be part of the data.

i = the index (ranking or position of a data value)

n = the total number of data

• Order the data from smallest to largest.
• Calculate i = 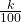(n+1).
• If i is an integer, then the kth percentile is the data value in the ith position in the ordered set of data.
• If i is not an integer, then round i up and round i down to the nearest integers. Average the two data values in these two positions in the ordered dataset. This is easier to understand in an example.

Finding the Percentile of a Value in a Dataset

The process for finding the corresponding percentile of a given observation is as follows:

x = the number of data values counting from the bottom of the data list up to (but not including) the data value for which you want to find the percentile

y = the number of data values equal to the data value (repeated values) for which you want to find the percentile

n = the total number of data

• Order the data from smallest to largest.
• Calculate 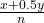(100). Then round to the nearest integer.

Quartiles

Quartiles also deal with an ordered dataset and are really just special percentiles. The first quartile, Q₁, is the same as the 25th percentile. The second quartile, Q₂, is the same as the 50th percentile and is also called the median. The third quartile, Q₃, is the same as the 75th percentile.

The Median

The median is a number that measures the “halfway point” of the data. You can think of the median as the “middle value,” but it does not actually have to be one of the observed values. It is a number that separates ordered data into halves. Half the values are the same number or smaller than the median, and half the values are the same number or larger. For example, consider the following data:

1, 11.5, 6, 7.2, 4, 8, 9, 10, 6.8, 8.3, 2, 2, 10, 1

Ordered from smallest to largest:

1, 1, 2, 2, 4, 6, 6.8, 7.2, 8, 8.3, 9, 10, 10, 11.5

Since there are 14 observations, the median is between the seventh value, 6.8, and the eighth value, 7.2. To find the median, we must interpolate, or split the difference. In this case we simply add both values together and divide by two.

The median is 7. Half of the values are smaller than 7, and half of the values are larger than 7.

Depending on the context, the median could be both a measure of location and/or center. Future sections will further discuss the median and using it as a measure of center.

Finding Quartiles

Quartiles can be found by treating them either as a percentile or in a similar fashion to the median. They may or may not be part of the data. To find the quartiles, first find the median, or second quartile. The first quartile, Q₁, can be treated as the middle value (or median) of the lower half of the data. The third quartile, Q₃, can be treated as the middle value (or median) of the upper half of the data. To get the idea, consider the same dataset as above, where the median is 7.

1, 1, 2, 2, 4, 6, 6.8, 7.2, 8, 8.3, 9, 10, 10, 11.5

The median divides the dataset into two halves, with 7 observations in each half (pictured in different colors below). The first quartile is 2 and the third quartile is 9.

1, 1, 2, 2, 4, 6, 6.8, 7.2, 8, 8.3, 9, 10, 10, 11.5

In this example there are an even number of observations and we had to interpolate the median. This divided our dataset into two halves, with an odd amount of numbers in each half, meaning the quartiles were part of the data set. In other cases, if the median divides your dataset into two even halves you must interpolate the quartiles. Rather than splitting the difference, it is often more appropriate to treat Q₁ and Q₃ as the 25^th and 75^th percentiles, respectively.

Interpreting Percentiles, Quartiles, and Median

A percentile indicates the relative standing of a data value when data are sorted into numerical order from smallest to largest. Percentages of data values are less than or equal to the pth percentile. For example, 15% of data values are less than or equal to the 15th percentile.

• Low percentiles always correspond to lower data values.
• High percentiles always correspond to higher data values.

A percentile may or may not correspond to a value judgment about whether it is “good” or “bad.” The interpretation of whether a certain percentile is “good” or “bad” depends on the context of the situation to which the data applies. In some situations, a low percentile would be considered “good”; in other contexts, a high percentile might be considered “good.” In many situations, there is no value judgment that applies.

Understanding how to interpret percentiles properly is important not only when describing data but also when calculating probabilities, like those you’ll find in later chapters of this text.

Five-Number Summary

The five-number summary is a simple, easy way to quickly summarize a dataset. It is also the first step to identifying any outliers. It consists of:

1. Minimum
2. Q₁
3. Median
4. Q₃
5. Maximum

Interquartile Range

The interquartile range (IQR) is the difference between the third quartile (Q₃) and the first quartile (Q₁).

IQR = Q₃ – Q₁

The IQR is also helpful to determine potential outliers and can be used as a measure of spread.

Fence Rule

Although points may often look like outliers on a graph, we establish the upper fence (UF) and lower fence (LF) to numerically decide if a value is an outlier. The lower fence is 1.5 times the IQR subtracted from the first quartile (LF = Q₁ – 1.5*IQR), while the upper fence is 1.5 times the IQR added to the third quartile (UF = Q₃ + 1.5*IQR). If a value falls outside of these fences—i.e., less than the lower fence or greater than the upper fence—we will flag it as an outlier.

A potential outlier is a data point that is significantly different from the other data points. These special data points may be errors or some kind of abnormality, or they may be a key to understanding the data. Potential outliers always require further investigation.

Box Plots

Box plots (also called box-and-whisker plots or box-whisker plots) give a good graphical image of the concentration of the data. They also show how far the extreme values are from most of the data. A box plot is constructed from the values of the five-number summary, which we use to compare how close they are to other data values.

To construct a box plot, use a horizontal or vertical number line and a rectangular box. The smallest and largest data values serve as the endpoints of the axis. The first quartile marks one end of the box, and the third quartile marks the other end of the box. Approximately the middle 50% of the data values fall inside the box. The “whiskers” extend from the ends of the box to the smallest and largest data values. The second quartile, or median, can be between the first and third quartiles, or it can be one, the other, or both. The box plot gives a good, quick picture of the data.

Example

Consider, again, this dataset.

1, 1, 2, 2, 4, 6, 6.8, 7.2, 8, 8.3, 9, 10, 10, 11.5

The first quartile is 2, the median is 7, and the third quartile is 9. The smallest value is 1, and the largest value is 11.5. The following image shows the constructed box plot.

 

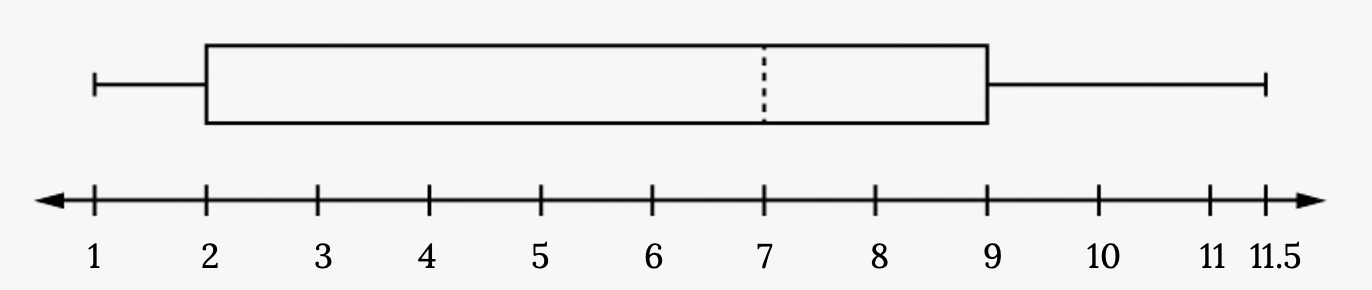
The two whiskers extend from the first quartile to the smallest value and from the third quartile to the largest value. The median is shown with a dashed line.

NOTE: It is important to start a box plot with a scaled number line. Otherwise the box plot may not be useful.

Example

The following data are the heights of 40 students in a statistics class.

59, 60, 61, 62, 62, 63, 63, 64, 64, 64, 65, 65, 65, 65, 65, 65, 65, 65, 65, 66, 66, 67, 67, 68, 68, 69, 70, 70, 70, 70, 70, 71, 71, 72, 72, 73, 74, 74, 75, 77

Construct a box plot with the following properties.

• Minimum value = 59
• Maximum value = 77
• First quartile (Q1) = 64.5
• Second quartile (Q2 or median) = 66
• Third quartile (Q3) = 70

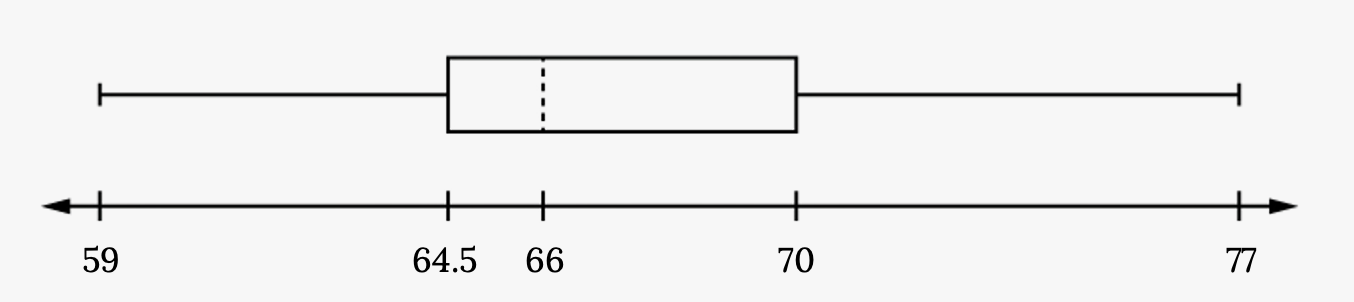
1. Each quarter has approximately 25% of the data.
2. The spreads of the four quarters are 64.5 – 59 = 5.5 (first quarter), 66 – 64.5 = 1.5 (second quarter), 70 – 66 = 4 (third quarter), and 77 – 70 = 7 (fourth quarter). So, the second quarter has the smallest spread, and the fourth quarter has the largest spread.
3. Range: 77 – 59 = 18 (maximum value – minimum value)
4. Interquartile range: 70 – 64.5 = 5.5 (Q3 – Q1)
5. The interval 59–65 has more than 25% of the data, so it has more data in it than the interval 66–70, which has 25% of the data.
6. The middle 50% (middle half) of the data has a range of 5.5 inches.

For some sets of data, some values (i.e., the largest value, smallest value, first quartile, median, or third quartile) may be the same. For instance, you might have a dataset in which the median and the third quartile are the same. In this case, the diagram would not have a dotted line inside the box displaying the median. The right side of the box would display both the third quartile and the median. For example, if the smallest value and the first quartile were both 1, the median and the third quartile were both 5, and the largest value was 7, the box plot would look like:

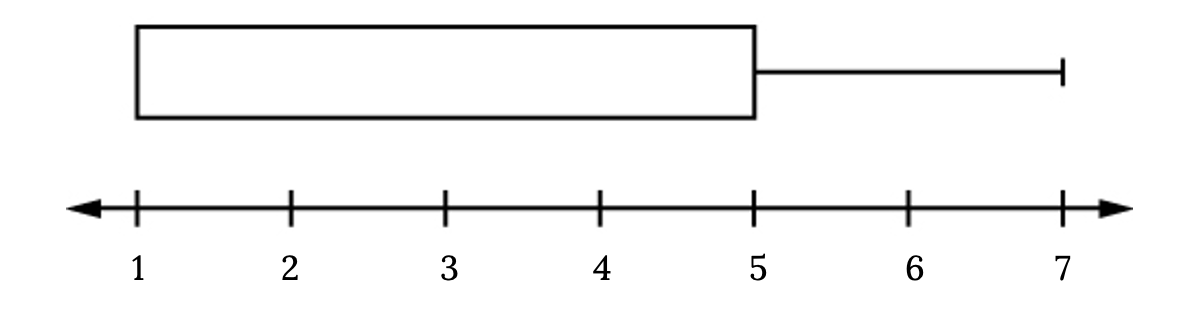
In this case, at least 25% of the values are equal to 1. Twenty-five percent of the values are between 1 and 5, inclusive. At least 25% of the values are equal to 5. The top 25% of the values fall between 5 and 7, inclusive.

Figure References

Figure 2.42: Kindred Grey (2020). Box plot. CC BY-SA 4.0. Adaptation of Figure 2.11 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/2-4-box-plots

Figure 2.43: Kindred Grey (2020). Student heights (box plot). CC BY-SA 4.0. Adaptation of Figure 2.12 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/2-4-box-plots

Figure 2.44: Kindred Grey (2020). Box plot with the same values. CC BY-SA 4.0. Adaptation of Figure 2.13 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/2-4-box-plots

Figure Descriptions

Figure 2.42: Horizontal box plot’s first whisker extends from the smallest value, 1, to the first quartile, 2, the box begins at the first quartile and extends to the third quartile, 9, a vertical dashed line is drawn at the median, 7, and the second whisker extends from the third quartile to the largest value of 11.5.

Figure 2.43: Horizontal box plot with first whisker extending from smallest value, 59, to Q1, 64.5, box beginning from Q1 to Q3, 70, median dashed line at Q2, 66, and second whisker extending from Q3 to largest value, 77.

Figure 2.44: Horizontal box plot box begins at the smallest value and Q1, 1, until the Q3 and median, 5, no median line is designated, and has its lone whisker extending from the Q3 to the largest value, 7.