2.6 Measures of Center
Let’s keep working through the acronym SOCS for describing key aspects of our data, this time focusing on the center.
- Shape
- Outliers
- Center
- Spread
The “center” is a way of describing the “central tendency” or “typical value” of a dataset. The two most widely used measures of the center of the data are the mean (average) and the median. Most people are familiar with the ideas of these two: (1) to calculate the mean weight of 50 people, add the 50 weights together and divide by 50, and (2) to find the median weight of the 50 people, order the data and find the number that splits the data into two equal parts.
However, some datasets may be better summarized by one or the other. The most “appropriate” measure of center depends on the shape of the distribution and the presence of extreme values or potential outliers.
The Mean
The mean is the most common measure of the center. The words “mean” and “average” are often used interchangeably. The technical term is “arithmetic mean,” and “average” technically refers to a center location. However, in practice among non-statisticians, “average” is commonly accepted for “arithmetic mean.”
When each value in the dataset is not unique, the mean can be calculated by multiplying each distinct value by its frequency and then dividing the sum by the total number of data values. The sample mean is denoted by an x with a bar over it, ![]() , pronounced simply “x bar.”
, pronounced simply “x bar.”
The Greek letter μ (pronounced “mew”) represents the population mean. We will often use the sample mean to estimate the population mean. One of the requirements for the sample mean to be a good estimate of the population mean is for the sample to be taken truly at random.
Example
Calculate the mean of the sample: 1, 1, 1, 2, 2, 3, 4, 4, 4, 4, 4.
Solution
![]() = (1+1+1+2+2+3+4+4+4+4+4)/11 = 2.7
= (1+1+1+2+2+3+4+4+4+4+4)/11 = 2.7
Your Turn!
Solution
![]() = (7+10+14+14+15+21+38+38+38+56)/10 = 25.1
= (7+10+14+14+15+21+38+38+38+56)/10 = 25.1
The Median
The median is generally a better measure of the center when there are extreme values or outliers because it is more robust, or not affected by the precise numerical values of those outliers.
Especially for larger datasets, you may choose to use the following location function over the traditional counting method to find the median:
![]() .
.
Remember that this function simply tells you where to look for the median, not the actual value itself, and n is the total number of data values in the sample (sample size).
Once you a have arranged your data in ascending order (smallest to largest), the method of finding your median will differ slightly based on whether you have an odd or even sample size. If n is odd, the median is included in the dataset and is simply the middle value found using the location function. If n is an even number, your location function will give you a decimal value ending in .5, and to find the median, you must calculate the average of the numbers in the ![]() and
and ![]() + 1 positions.
+ 1 positions.
For example, if the total number of data values is 97, then ![]() =
= ![]() = 49. The median is the 49th value in the ordered data. If the total number of data values is 100, then
= 49. The median is the 49th value in the ordered data. If the total number of data values is 100, then ![]() =
= ![]() = 50.5. The median occurs midway between the 50th and 51st values. The location of the median and the value of the median are not the same. The upper case letter M is often used to represent the median. The next example illustrates the location of the median and the value of the median.
= 50.5. The median occurs midway between the 50th and 51st values. The location of the median and the value of the median are not the same. The upper case letter M is often used to represent the median. The next example illustrates the location of the median and the value of the median.
Example
AIDS data indicating the number of months a patient with AIDS lives after taking a new antibody drug are as follows (smallest to largest): 3, 4, 8, 8, 10, 11, 12, 13, 14, 15, 15, 16, 16, 17, 17, 18, 21, 22, 22, 24, 24, 25, 26, 26, 27, 27, 29, 29, 31, 32, 33, 33, 34, 34, 35, 37, 40, 44, 44, 47. Calculate the median.
Solution
To find the median, M, first use the formula for the location. The location is:
![]() =
= ![]() = 20.5
= 20.5
Starting at the smallest value, the median is located between the 20th and 21st values (the two 24s):
3, 4, 8, 8, 10, 11, 12, 13, 14, 15, 15, 16, 16, 17, 17, 18, 21, 22, 22, 24, 24, 25, 26, 26, 27, 27, 29, 29, 31, 32, 33, 33, 34, 34, 35, 37, 40, 44, 44, 47
M = ![]() = 24
= 24
Your Turn!
Calculate the median of the sample: 7, 10, 14, 14, 15, 21, 38, 38, 38, 56.
The Mode
Another measure of the center is the mode. The mode is the most frequent value. There can be more than one mode in a dataset as long as those values have the same frequency and that frequency is the highest. A dataset with two modes is called bimodal. For example, if five real estate exam scores are 430, 430, 480, 480, 495, then the dataset is bimodal because the scores 430 and 480 each occur twice.
When is the mode the best measure of the “center”? Consider a weight loss program that advertises a mean weight loss of six pounds during the first week of the program. The mode might indicate that most people lose two pounds the first week, making the program less appealing.
NOTE:
The mode can be calculated for categorical data as well as quantitative data but has different uses and interpretations for each. For example:
- If we had the categorical dataset {red, red, red, green, green, yellow, purple, black, blue}, the mode is red. This is useful to us.
- If we had the quantitative dataset {1.0, 2.1, 2.1, 5.0, 5.1, 5.5, 5.7, 6.1, 6.2, 6.4, 6.6, 7.1, 7.8, 8.1, 8.9}, the numerical mode is 2.1, but that does not do a good job of telling us about the actual modality, or where the data is clustered.
Example
Statistics exam scores for 20 students are as follows:
50, 53, 59, 59, 63, 63, 72, 72, 72, 72, 72, 76, 78, 81, 83, 84, 84, 84, 90, 93
Find the mode.
Solution
The most frequent score is 72, which occurs five times. Mode = 72.
Order Relationship of Measures of Center
Consider the following dataset: 4, 5, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 8, 9, 10.
This dataset can be represented by the histogram in Figure 2.45. Each interval has a width of one, and each value is located in the middle of an interval.
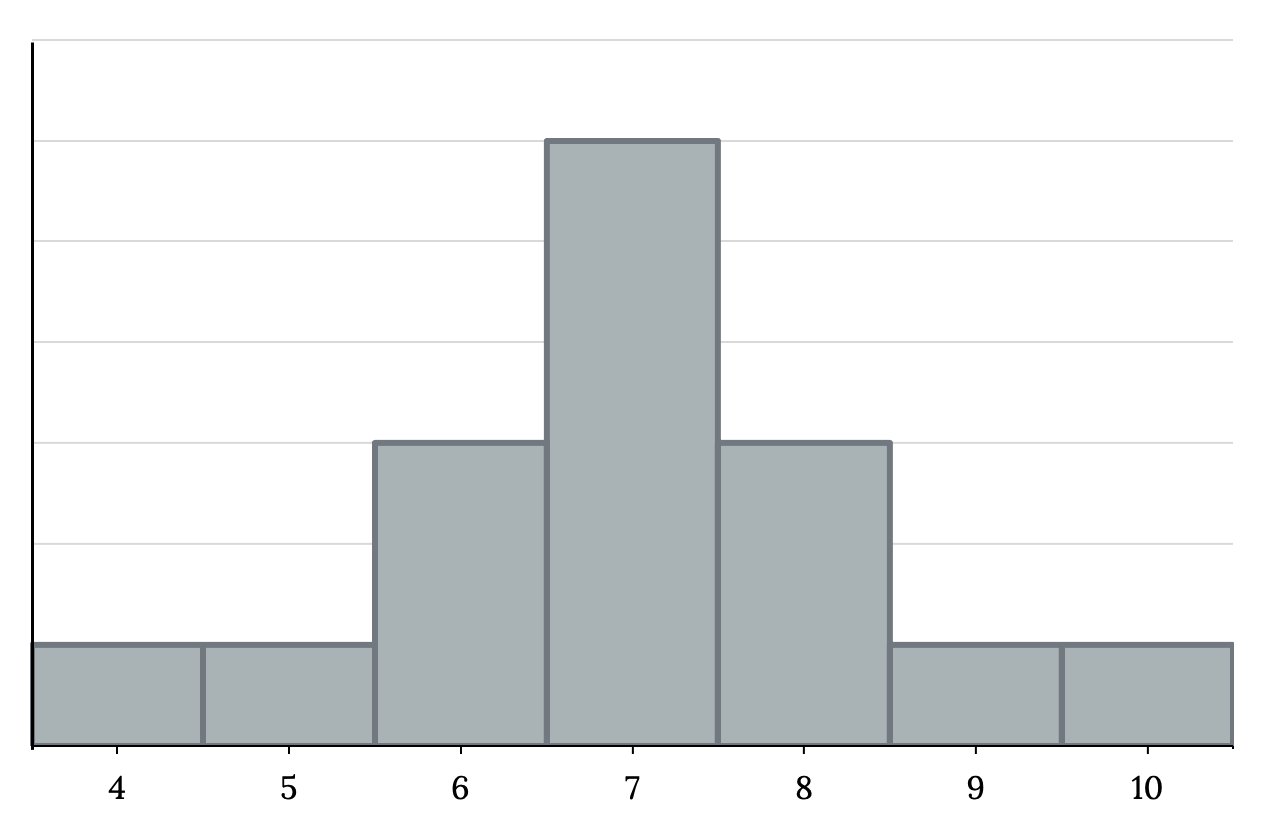
The histogram displays a symmetrical distribution of data. A distribution is symmetrical if a vertical line can be drawn at some point in the histogram such that the shapes to the left and the right of the vertical line are mirror images of each other. The mean, the median, and the mode are each 7 for these data. In a perfectly symmetrical distribution, the mean and the median are the same. This example has one mode (unimodal), and the mode is the same as the mean and median. In a symmetrical distribution that has two modes (bimodal), the two modes would be different from the mean and median.
The histogram for the data {4, 5, 6, 6, 6, 7, 7, 7, 7, 8} is not symmetrical. The right-hand side seems “chopped off” compared to the left side. A distribution of this type is said to be skewed to the left because it is pulled out to the left.
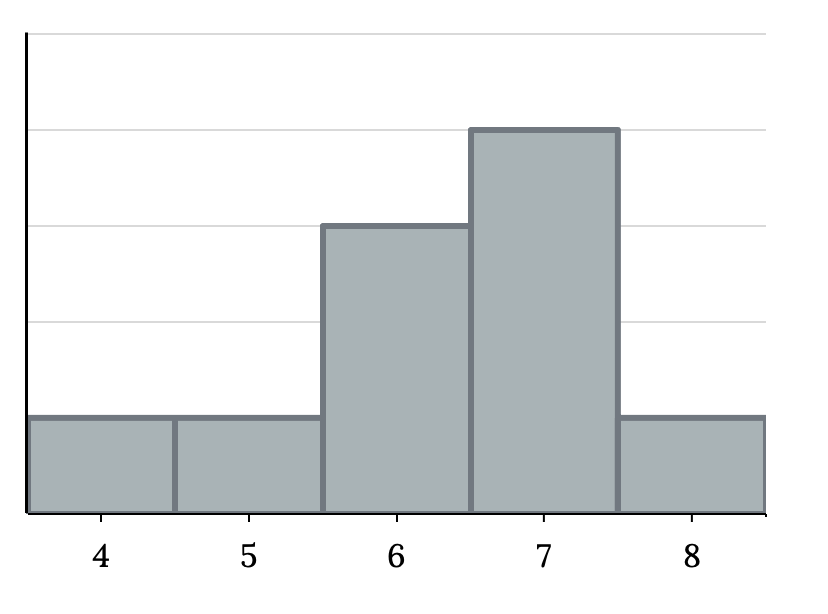
The mean is 6.3, the median is 6.5, and the mode is 7. Notice that the mean is less than the median, and they are both less than the mode. The mean and the median both reflect the skewing, but the mean reflects it more so.
The histogram for the data {6, 7, 7, 7, 7, 8, 8, 8, 9, 10} is also not symmetrical. It is skewed to the right.
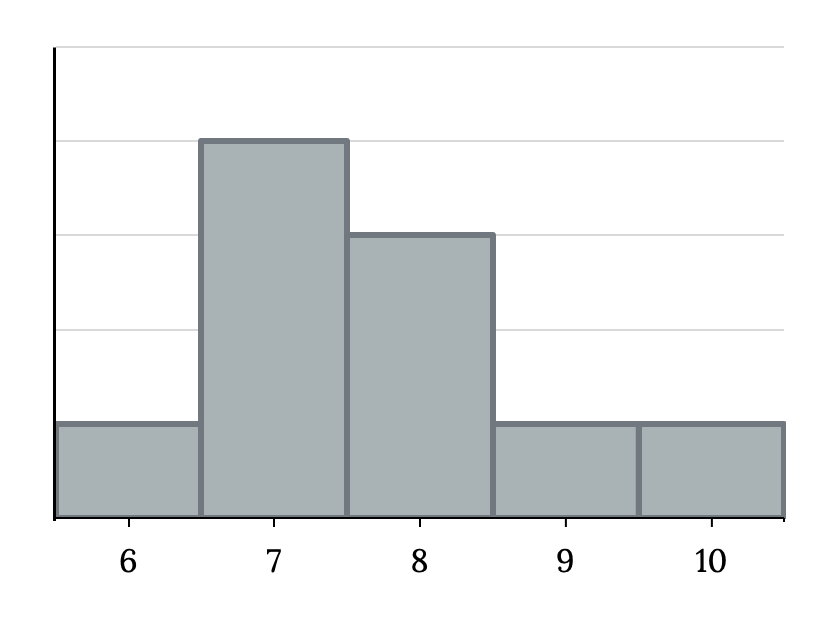
The mean is 7.7, the median is 7.5, and the mode is 7. Of the three statistics, the mean is the largest, while the mode is the smallest. Again, the mean reflects the skewing the most.
To summarize, if the distribution of data is skewed to the left, the mean is often less than the median, which is often less than the mode. If the distribution of data is skewed to the right, the mode is often less than the median, which is less than the mean.
Skewness and symmetry become important when we discuss probability distributions in later chapters.
Example
Statistics are used to compare and sometimes identify authors. The following lists shows a simple random sample that compares the letter counts for three authors.
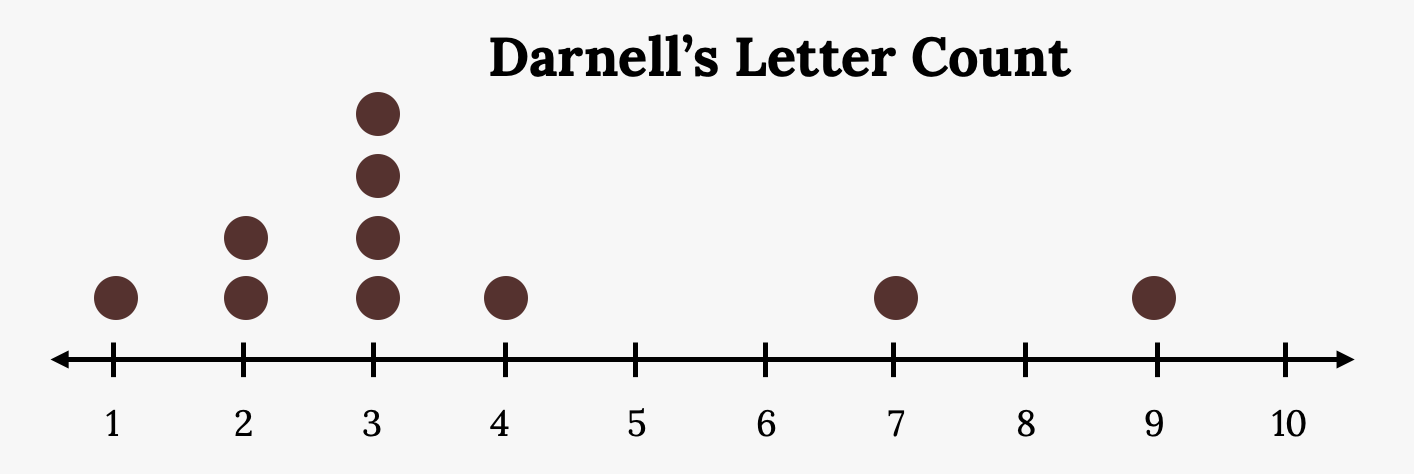
Darnell: 7, 9, 3, 3, 3, 4, 1, 3, 2, 2
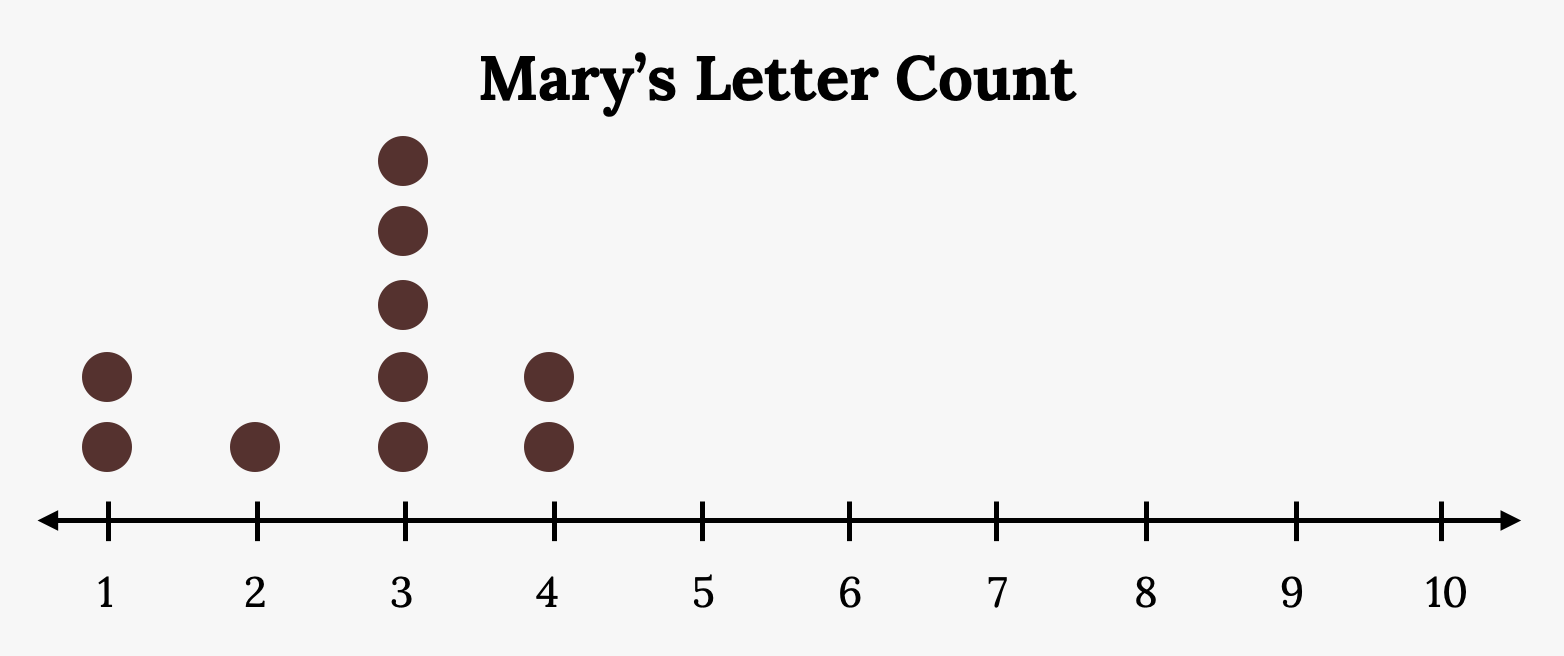
Mary: 3, 3, 3, 4, 1, 4, 3, 2, 3, 1
Lee: 2, 3, 4, 4, 4, 6, 6, 6, 8, 3
Make a dot plot for the three authors and compare the shapes.
Darnell’s distribution has a right (positive) skew:
Mary’s distribution has a left (negative) skew:
Lee’s distribution is symmetrically shaped:

Calculate the mean for each.
Solution
Darnell’s mean is 3.7. Mary’s mean is 2.7. Lee’s mean is 4.6.
Calculate the median for each.
Solution
Darnell’s median is three. Mary’s median is three. Lee’s median is four.
Describe any pattern you notice between the shape and the measures of center.
Solution
It appears that the median is closest to the high point (the mode), while the mean tends to be farther out on the tail. In a symmetrical distribution, the mean and the median are both centrally located close to the high point of the distribution.
Your Turn!
Suppose that in a small town of 50 people, one person earns $5,000,000 per year, and the other 49 each earn $30,000. Which is the better measure of the “center,” the mean or the median?
Solution
x = ![]() = 129,400
= 129,400
M = 30,000
There are 49 people who earn $30,000 and 1 person who earns $5,000,000. The median is a better measure of the center than the mean because 49 of the values are $30,000 and one is $5,000,000. The $5,000,000 is an outlier. The $30,000 gives us a better sense of the middle of the data.
Calculating the Mean of Grouped Frequency Tables
When only grouped data is available, we do not know the individual data values (only the intervals and interval frequencies); therefore, we cannot compute an exact mean for the dataset. What we must do is estimate the actual mean by calculating the mean of a frequency table (a data representation in which grouped data is displayed along with the corresponding frequencies). To calculate the mean from a grouped frequency table, we can apply the basic definition of mean:
![]() .
.
We simply need to modify the definition to fit within the restrictions of a frequency table. Since we do not know the individual data values, we can instead find the midpoint of each interval. The midpoint is:
![]() .
.
We can now modify the mean definition to be:
![]()
where f = the frequency of the interval and m = the midpoint of the interval.
Example
A frequency table displaying professor Blount’s last statistic test is shown. Find the best estimate of the class mean.
| Grade interval | Number of students |
|---|---|
| 50–56.5 | 1 |
| 56.5–62.5 | 0 |
| 62.5–68.5 | 4 |
| 68.5–74.5 | 4 |
| 74.5–80.5 | 2 |
| 80.5–86.5 | 3 |
| 86.5–92.5 | 4 |
| 92.5–98.5 | 1 |
Figure 2.51: Blount’s statistics test
Find the midpoints for all intervals.
Solution
| Grade interval | Midpoint |
|---|---|
| 50–56.5 | 53.25 |
| 56.5–62.5 | 59.5 |
| 62.5–68.5 | 65.5 |
| 68.5–74.5 | 71.5 |
| 74.5–80.5 | 77.5 |
| 80.5–86.5 | 83.5 |
| 86.5–92.5 | 89.5 |
| 92.5–98.5 | 95.5 |
Figure 2.52: Midpoint
Calculate the sum of the product of each interval frequency.
Solution
![]() fm = 53.25(1) + 59.5(0) + 65.5(4) + 71.5(4) + 77.5(2) + 83.5 (3) + 89.5(4) + 95.5(1) = 1,460.25
fm = 53.25(1) + 59.5(0) + 65.5(4) + 71.5(4) + 77.5(2) + 83.5 (3) + 89.5(4) + 95.5(1) = 1,460.25
Calculate the midpoint.
Solution
![]() =
= ![]() =
= ![]() = 76.86
= 76.86
Your Turn!
Maris conducted a study on the effect that playing video games has on memory recall. As part of her study, she compiled the following data:
| Hours teenagers spend on video games | Number of teenagers |
|---|---|
| 0–3.5 | 3 |
| 3.5–7.5 | 7 |
| 7.5–11.5 | 12 |
| 11.5–15.5 | 7 |
| 15.5–19.5 | 9 |
Figure 2.53: Video game data
What is the best estimate for the mean number of hours spent playing video games?
Additional Resources
Figure References
Figure 2.45: Kindred Grey (2020). Symmetrical distribution. CC BY-SA 4.0.
Figure 2.46: Kindred Grey (2020). Skewed left. CC BY-SA 4.0.
Figure 2.47: Kindred Grey (2020). Skewed right. CC BY-SA 4.0.
Figure 2.48: Kindred Grey (2020). Darnell’s letter count. CC BY-SA 4.0. Adaptation of Figure 2.21 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-6-skewness-and-the-mean-median-and-mode
Figure 2.49: Kindred Grey (2020). Mary’s letter count. CC BY-SA 4.0. Adaptation of Figure 2.22 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-6-skewness-and-the-mean-median-and-mode
Figure 2.50: Kindred Grey (2020). Lee’s letter count. CC BY-SA 4.0. Adaptation of Figure 2.23 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-6-skewness-and-the-mean-median-and-mode
Figure Descriptions
Figure 2.45: Histogram that matches the supplied data. It consists of seven adjacent bars with the x-axis split into intervals of one from four to 10. The heights of the bars peak in the middle and taper symmetrically to the right and left.
Figure 2.46: Histogram that matches the supplied data. It consists of five adjacent bars with the x-axis split into intervals of one from four to eight. The peak is to the right, and the heights of the bars taper down to the left.
Figure 2.47: Histogram that matches the supplied data. It consists of five adjacent bars with the x-axis split into intervals of one from six to 10. The peak is to the left, and the heights of the bars taper down to the right.
Figure 2.48: Dot plot that matches the supplied data for Darnell. The plot uses a number line from one to 10. It shows one x over one, two x’s over two, four x’s over three, one x over four, one x over seven, and one x over nine. There are no x’s over the numbers five, six, eight, and 10.
Figure 2.49: Dot plot that matches the supplied data for Mary. The plot uses a number line from one to 10. It shows two x’s over one, one x over two, five x’s over three, and two x’s over four. There are no x’s over the numbers five, six, seven, eight, nine, and 10.
Figure 2.50: Dot plot that matches the supplied data for Lee. The plot uses a number line from one to 10. It shows one x over two, two x’s over three, three x’s over four, three x’s over six, and one x over eight. There are no x’s over the numbers one, five, seven, nine, and 10.
A number that measures the central tendency of the data
The middle number in a sorted list
The arithmetic mean, or average, of a dataset
The arithmetic mean, or average, of a population
Not affected by violations of assumptions such as outliers
The most frequently occurring value
How many peaks or clusters there appear to be in a quantitative distribution

