7.3 Inference for Two-Sample Proportions

Comparing two proportions, like comparing two means, is also very common when we are working with categorical data. If our parameter of inference is p1 – p2, then we can estimate it with \hat{p}_{1} – \hat{p}_{2}.

When conducting inference on two independent population proportions, the following characteristics should be present:

  • The two independent samples are simple random samples that are independent.
  • For each of the samples, the number of successes is at least five, and the number of failures is at least five.
  • Growing literature states that the population must be at least ten or 20 times the size of the sample. This keeps each population from being over-sampled and causing incorrect results.

Sampling Distribution of the Difference in Two Proportions

We can build a sampling distribution for \hat{p}_{1} – \hat{p}_{2} similar to what we did for the difference in two independent sample means. The difference of two proportions follows an approximate normal distribution. We will wait to show the standard error and sampling distribution because we calculate them slightly differently for hypothesis tests and confidence intervals.

Hypothesis Test for the Difference in Two Proportions

If two estimated proportions are different, it may be due to a difference in the populations, or it may be due to chance. A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the population proportions.

Generally, the null hypothesis states that the two proportions are the same (i.e., H0: p1 = p2). Since we are assuming there is no difference in the null, we can use both samples to estimate the pooled proportion, pp , calculated as follows:

pp = \frac{{x}_{1}+{x}_{2}}{{n}_{1}+{n}_{2}}

We can use this pooled proportion in the calculation of our z-test statistic:

z = \frac{\left({\hat{p}}_{1}-{\hat{p}}_{2}\right)-\left({p}_{1}-{p}_{2}\right)}{\sqrt{{p}_{p}\left(1-{p}_{p}\right)\left(\frac{1}{{n}_{1}}+\frac{1}{{n}_{2}}\right)}}

Example

Two types of medication for hives are being tested to determine if there is a difference in the proportions of adult patient reactions. Twenty out of a random sample of 200 adults given Medication A still had hives 30 minutes after taking the medication. Twelve out of another random sample of 200 adults given Medication B still had hives 30 minutes after taking the medication. Test at a 1% level of significance.

Solution

The problem asks for a difference in proportions, making it a test of two proportions.

Let A and B be the subscripts for medication A and medication B, respectively. Then pA and pB are the desired population proportions.

Random variable: \hat{p}_{A} – \hat{p}_{B} = difference in the proportions of adult patients who did not react after 30 minutes to medication A and to medication B.

H0: \hat{p}_{A} = \hat{p}_{B} or \hat{p}_{A} – \hat{p}_{B} = 0

HA: \hat{p}_{A} ≠ \hat{p}_{B} or \hat{p}_{A} – \hat{p}_{B} ≠ 0

The words “is a difference” tell you the test is two-tailed.

Distribution for the test:

Since this is a test of two binomial population proportions, the distribution is normal.

Find the pooled proportion: pp

pp = \frac{x_A+x_B}{n_A+n_B} = \frac{20+12}{200+200} = 0.08 

1 – pp = 0.92

\hat{p}_{A} – \hat{p}_{B} follows an approximate normal distribution.

Calculate the p-value using the normal distribution:

p-value = 0.1404

Estimated proportion for group A: \hat{p}_{A} = \frac{x_A}{n_A} = \frac{20}{200} = 0.1

Estimated proportion for group B: \hat{p}_{B} = \frac{x_B}{n_B} = \frac{12}{200} = 0.06

 

 

 

 

 

 

 

 

 

Graph:

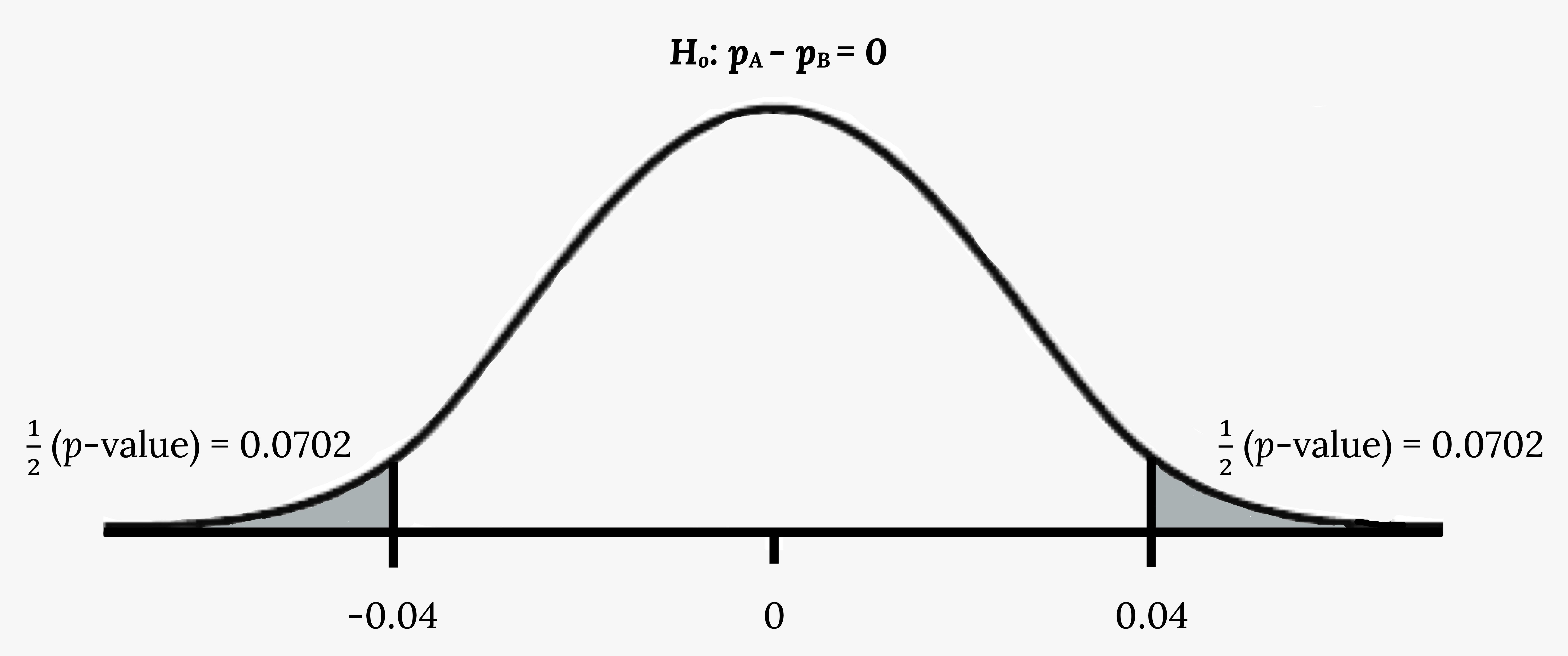
Figure description available at the end of the section.
Figure 7.8: Medications A and B. Figure description available at the end of the section.

\hat{p}_{A} – \hat{p}_{B} = 0.1 – 0.06 = 0.04.

Half the p-value is below –0.04, and half is above 0.04.

Compare α and the p-value: 

α = 0.01 and the p-value = 0.1404. α < p-value.

Make a decision:

Since α < p-value, do not reject H0.

Conclusion: At a 1% level of significance, from the sample data, there is not sufficient evidence to conclude that there is a difference in the proportions of adult patients who did not react after 30 minutes to medication A and medication B.

Your Turn!

Two types of valves are being tested to determine if there is a difference in pressure tolerances. For Valve A, 15 out of a random sample of 100 cracked under 4,500 psi. For Valve B, six out of a random sample of 100 cracked under 4,500 psi. Test at a 5% level of significance.

 

 

Confidence Intervals for the Difference in Two Proportions

Once we have identified the presence of a difference in a two-sample test, we may want to estimate it. Our confidence interval would be of the form (PE – MoE, PE + MoE), where our point estimate is \hat{p}_{1} – \hat{p}_{2}, and the MoE is made up of:

MoE = \left({z}_{\frac{\alpha }{2}}\right)\left(SE)

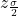  • {z}_{\frac{\sigma }{2}} is the z critical value with area to the right equal to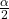 \frac{\alpha }{2}
  • SE \sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}
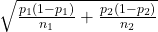
    • In the SE will we estimate p1 with 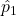\hat{p}_{1} and p2 with 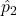\hat{p}_{2} if we do not know them.

Putting that all together, our formula for a CI to estimate the difference in two proportions will be:

\hat{p}_{1} – \hat{p}_{2}\pm\left({z}_{\frac{\alpha }{2}}\right)\sqrt{\frac{\hat{p}_{1}\text{(1-}\hat{p}_{1})}{n_1}+\frac{\hat{p}_{2}\text{(1-}\hat{p}_{2})}{n_2}}

Additional Resources

QR code

Click here for additional multimedia resources, including podcasts, videos, lecture notes, and worked examples.

If you are using an offline version of this text, access the resources for this section via the QR code, or by visiting https://doi.org/10.7294/26207456.

Figure References

Figure 7.8: Kindred Grey (2020). Medications A and B. CC BY-SA 4.0.

Figure Descriptions

Figure 7.8: Normal distribution curve of the difference in the percentages of adult patients who don’t react to medication A and B after 30 minutes. The mean is equal to zero, and the values -0.04, 0, and 0.04 are labeled on the horizontal axis. Two vertical lines extend from -0.04 and 0.04 to the curve. The region to the left of -0.04 and the region to the right of 0.04 are each shaded to represent 1/2(p-value) = 0.0702.

definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Significant Statistics: An Introduction to Statistics Copyright © 2024 by John Morgan Russell is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book