Chapter 2 Extra Practice
2.1 Descriptive Statistics and Frequency Distributions
- What are the two types of descriptive statistical methods?
2.2 Displaying and Describing Categorical Distributions
1. What are the two basic options for graphing categorical data?
2. When describing categorical data we want to note what two aspects?
3. When describing the level of variability in categorical data, we want to think about it as .
2.3 Displaying Quantitative Distributions
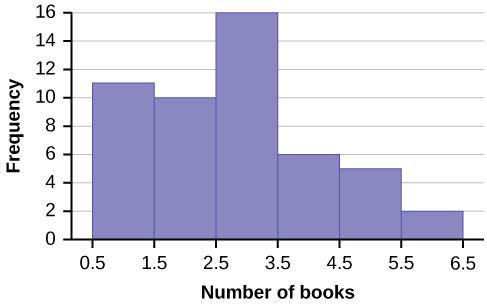
1. Create a histogram for the number of books bought by 50 part-time college students at ABC College. The number of books is discrete data since books are counted.
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
2, 2, 2, 2, 2, 2, 2, 2, 2, 2
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3
4, 4, 4, 4, 4, 4
5, 5, 5, 5, 5
6, 6
Eleven students buy one book. Ten students buy two books. Sixteen students buy three books. Six students buy four books. Five students buy five books. Two students buy six books.
Because the data are integers, subtract 0.5 from 1, the smallest data value, and add 0.5 to 6, the largest data value. Then the starting point is 0.5, and the ending value is 6.5.
Next calculate the width of each bar or class interval. If the data are discrete, and there are not too many different values, a width that places the data values in the middle of the bar or class interval is the most convenient.
Calculate the number of bars as follows:
![]() = 1
= 1
1 is the width of a bar. Therefore, bars = 6.
The following histogram displays the number of books on the x-axis and the frequency on the y-axis.
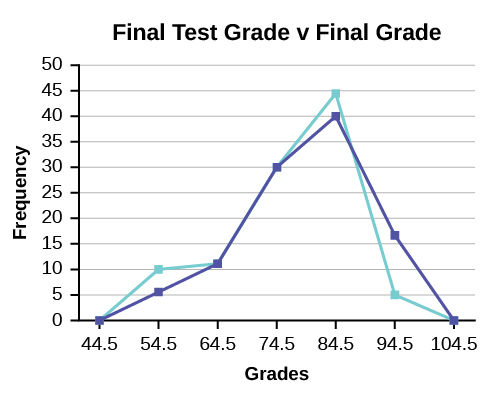
2. We will construct an overlay frequency polygon comparing the scores from the figure below with the students’ final numeric grades.
| Lower bound | Upper bound | Frequency | Cumulative frequency |
|---|---|---|---|
| 49.5 | 59.5 | 5 | 5 |
| 59.5 | 69.5 | 10 | 15 |
| 69.5 | 79.5 | 30 | 45 |
| 79.5 | 89.5 | 40 | 85 |
| 89.5 | 99.5 | 15 | 100 |
Figure 2.60: Frequency distribution for calculus final test scores
| Lower bound | Upper bound | Frequency | Cumulative frequency |
|---|---|---|---|
| 49.5 | 59.5 | 10 | 10 |
| 59.5 | 69.5 | 10 | 20 |
| 69.5 | 79.5 | 30 | 50 |
| 79.5 | 89.5 | 45 | 95 |
| 89.5 | 99.5 | 5 | 100 |
Figure 2.61: Frequency distribution for calculus final test scores
3. Construct a frequency polygon of US Presidents’ ages at inauguration shown in the figure below.[1]
| Age at inauguration | Frequency |
|---|---|
| 41.5–46.5 | 4 |
| 46.5–51.5 | 11 |
| 51.5–56.5 | 14 |
| 56.5–61.5 | 9 |
| 61.5–66.5 | 4 |
| 66.5–71.5 | 3 |
Figure 2.63
4. Construct frequency polygons for the following datasets:
| Pulse rates for women | Frequency |
|---|---|
| 60–69 | 12 |
| 70–79 | 14 |
| 80–89 | 11 |
| 90–99 | 1 |
| 100–109 | 1 |
| 110–119 | 0 |
| 120–129 | 1 |
Figure 2.64
| Actual speed in a 30 MPH zone | Frequency |
|---|---|
| 42–45 | 25 |
| 46–49 | 14 |
| 50–53 | 7 |
| 54–57 | 3 |
| 58–61 | 1 |
Figure 2.65
| Tar (mg) in non-filtered cigarettes | Frequency |
|---|---|
| 10–13 | 1 |
| 14–17 | 0 |
| 18–21 | 15 |
| 22–25 | 7 |
| 26–29 | 2 |
Figure 2.66
5. Construct a frequency polygon from the frequency distribution for the 50 highest-ranked countries for depth of hunger.[2]
| Depth of hunger | Frequency |
|---|---|
| 230–259 | 21 |
| 260–289 | 13 |
| 290–319 | 5 |
| 320–349 | 7 |
| 350–379 | 1 |
| 380–409 | 1 |
| 410–439 | 1 |
Figure 2.67
6. Use the two frequency tables to compare the life expectancies of men and women from 20 randomly selected countries. Include an overlaid frequency polygon, and discuss the shapes of the distributions, the center, the spread, and any outliers. What can we conclude about the life expectancy of women compared to men?[3]
| Life expectancy at birth (women) | Frequency |
|---|---|
| 49–55 | 3 |
| 56–62 | 3 |
| 63–69 | 1 |
| 70–76 | 3 |
| 77–83 | 8 |
| 84–90 | 2 |
Figure 2.68
| Life expectancy at birth (men) | Frequency |
|---|---|
| 49–55 | 3 |
| 56–62 | 3 |
| 63–69 | 1 |
| 70–76 | 1 |
| 77–83 | 7 |
| 84–90 | 5 |
Figure 2.69
7. The following table is a portion of a dataset from www.worldbank.org. Use the table to construct a time series graph for CO2 emissions for the United States.[4]
| Ukraine | United Kingdom | United States | |
|---|---|---|---|
| 2003 | 352,259 | 540,640 | 5,681,664 |
| 2004 | 343,121 | 540,409 | 5,790,761 |
| 2005 | 339,029 | 541,990 | 5,826,394 |
| 2006 | 327,797 | 542,045 | 5,737,615 |
| 2007 | 328,357 | 528,631 | 5,828,697 |
| 2008 | 323,657 | 522,247 | 5,656,839 |
| 2009 | 272,176 | 474,579 | 5,299,563 |
Figure 2.70
8. Construct a times series graph for (a) the number of male births, (b) the number of female births, and (c) the total number of births.[5]
| Female | Male | Total | |
|---|---|---|---|
| 1855 | 45,545 | 47,804 | 93,349 |
| 1856 | 49,582 | 52,239 | 101,821 |
| 1857 | 50,257 | 53,158 | 103,415 |
| 1858 | 50,324 | 53,694 | 104,018 |
| 1859 | 51,915 | 54,628 | 106,543 |
| 1860 | 51,220 | 54,409 | 105,629 |
| 1861 | 52,403 | 54,606 | 107,009 |
| 1862 | 51,812 | 55,257 | 107,069 |
| 1863 | 53,115 | 56,226 | 109,341 |
| 1864 | 54,959 | 57,374 | 112,333 |
| 1865 | 54,850 | 58,220 | 113,070 |
| 1866 | 55,307 | 58,360 | 113,667 |
| 1867 | 55,527 | 58,517 | 114,044 |
| 1868 | 56,292 | 59,222 | 115,514 |
| 1869 | 55,033 | 58,321 | 113,354 |
| 1870 | 56,431 | 58,959 | 115,390 |
| 1871 | 56,099 | 60,029 | 116,128 |
| 1872 | 57,472 | 61,293 | 118,765 |
| 1873 | 58,233 | 61,467 | 119,700 |
| 1874 | 60,109 | 63,602 | 123,711 |
| 1875 | 60,146 | 63,432 | 123,578 |
Figure 2.71
9. The following datasets list the number of full-time police officers per 100,000 citizens along with homicides per 100,000 citizens for the city of Detroit, Michigan, during the period from 1961 to 1973.[6]
| 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 | 1970 | 1971 | 1972 | 1973 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Police | 260.35 | 269.8 | 272.04 | 272.96 | 272.51 | 261.34 | 268.89 | 295.99 | 319.87 | 341.43 | 356.59 | 376.69 | 390.19 |
| Homicides | 8.6 | 8.9 | 8.52 | 8.89 | 13.07 | 14.57 | 21.36 | 28.03 | 31.49 | 37.39 | 46.26 | 47.24 | 52.33 |
Figure 2.72
-
- Construct a double time series graph using a common x-axis for both sets of data.
- Which variable increased the fastest? Explain.
- Did Detroit’s increase in police officers have an impact on the murder rate? Explain.
2.5 Measures of Location and Outliers
1. Test scores for a college statistics class held during the day are 99, 56, 78, 55.5, 32, 90, 80, 81, 56, 59, 45, 77, 84.5, 84, 70, 72, 68, 32, 79, and 90. Test scores for a college statistics class held during the evening are 98, 78, 68, 83, 81, 89, 88, 76, 65, 45, 98, 90, 80, 84.5, 85, 79, 78, 98, 90, 79, 81, and 25.5.[7]
- Find the smallest and largest values, the median, and the first and third quartile for the day class.
- Find the smallest and largest values, the median, and the first and third quartile for the night class.
- For each dataset, what percentage of the data is between the smallest value and the first quartile? The first quartile and the median? The median and the third quartile? The third quartile and the largest value? What percentage of the data is between the first quartile and the largest value?
- Create a box plot for each set of data. Use one number line for both box plots.
- Which box plot has the widest spread for the middle 50% of the data (the data between the first and third quartiles)? What does this mean for that set of data in comparison to the other set of data?
2. The following dataset shows the heights in inches for the boys in a class of 40 students: 66, 66, 67, 67, 68, 68, 68, 68, 68, 69, 69, 69, 70, 71, 72, 72, 72, 73, 73, 74. The following dataset shows the heights in inches for the girls in a class of 40 students: 61, 61, 62, 62, 63, 63, 63, 65, 65, 65, 66, 66, 66, 67, 68, 68, 68, 69, 69, 69. Construct a box plot using a graphing calculator for each dataset, and state which box plot has the wider spread for the middle 50% of the data.
3. Graph a box-and-whisker plot for the data values shown.
10, 10, 10, 15, 35, 75, 90, 95, 100, 175, 420, 490, 515, 515, 790
The five numbers used to create a box-and-whisker plot are:
- Min: 10
- Q1: 15
- Med: 95
- Q3: 490
- Max: 790
4. Graph a box-and-whisker plot for the data values shown.
0, 5, 5, 15, 30, 30, 45, 50, 50, 60, 75, 110, 140, 240, 330
5. Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. Fourteen people answered that they generally sell three cars, 19 generally sell four cars, 12 generally sell five cars, 9 generally sell six cars, and 11 generally sell seven cars.
- Construct a box plot. Use a ruler to measure and scale accurately.
- Looking at your box plot, does it appear that the data are concentrated together, spread out evenly, or concentrated in some areas but not in others? How can you tell?
6. In a survey of 20-year-olds in China, Germany, and the United States, people were asked the number of foreign countries they had visited in their lifetimes. The following box plots display the results.
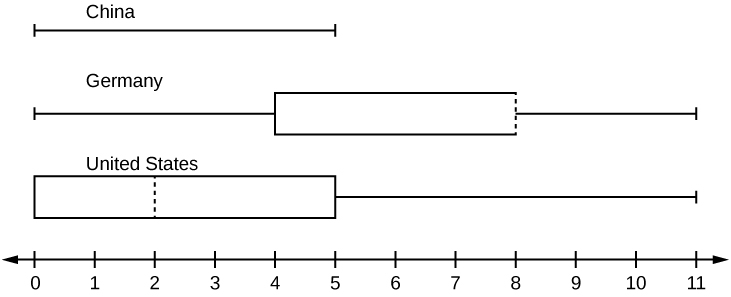
- In complete sentences, describe what the shape of each box plot implies about the distribution of the data collected.
- Have more Americans or more Germans surveyed been to over eight foreign countries?
- Compare the three box plots. What do the comparisons imply about the foreign travel of 20-year-old residents of the three countries?
7. Given the following box plot, answer the questions.

- Think of an example (in words) where the data might fit into the above box plot. In two-to-five sentences, write down the example.
- What does it mean to have the first and second quartiles so close together, while the second and third quartiles are far apart?
8. Given the following box plots, answer the questions.
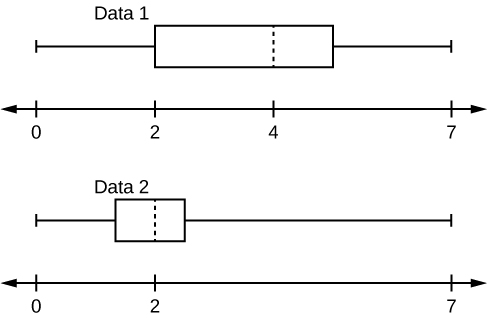
- In complete sentences, explain why each statement is false.
- Data 1 has more data values above two than Data 2 has above two.
- The datasets cannot have the same mode.
- For Data 1, there are more data values below four than there are above four.
- For which group, Data 1 or Data 2, is the value of 7 more likely to be an outlier? Explain why in complete sentences.
9. A survey was conducted of 130 purchasers of new BMW 3 Series cars, 130 purchasers of new BMW 5 Series cars, and 130 purchasers of new BMW 7 Series cars. In it, people were asked the age they were when they purchased their cars. The following box plots display the results.
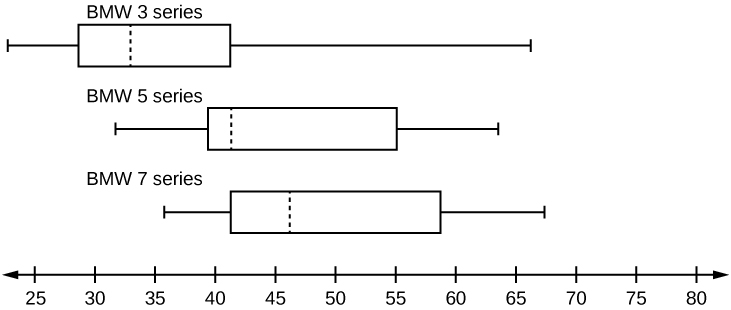
- In complete sentences, describe what the shape of each box plot implies about the distribution of the data collected for that car series.
- Which group is most likely to have an outlier? Explain.
- Compare the three box plots. What do they imply about ages when purchasing BMWs from different series?”
- Look at the BMW 5 Series. Which quarter has the smallest spread of data? What is the spread?
- Look at the BMW 5 Series. Which quarter has the largest spread of data? What is the spread?
- Look at the BMW 5 Series. Estimate the interquartile range (IQR).
- Look at the BMW 5 Series. Are there more data in the interval 31 to 38 or in the interval 45 to 55? How do you know this?
- Look at the BMW 5 Series. Which interval has the fewest data in it? How do you know this?
- 31–35
- 38–41
- 41–64
10. Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are as follows:
| Number of movies | Frequency |
|---|---|
| 0 | 5 |
| 1 | 9 |
| 2 | 6 |
| 3 | 4 |
| 4 | 1 |
Figure 2.77
Construct a box plot of the data.
11. Santa Clara County, CA, has approximately 27,873 Japanese-Americans. Their ages are as follows:
| Age group | Percent of community |
|---|---|
| 0–17 | 18.9 |
| 18–24 | 8.0 |
| 25–34 | 22.8 |
| 35–44 | 15.0 |
| 45–54 | 13.1 |
| 55–64 | 11.9 |
| 65+ | 10.3 |
Figure 2.78
- Construct a histogram of the Japanese-American community in Santa Clara County, CA. The bars will not be the same width for this example. Why not? What impact does this have on the reliability of the graph?
- What percentage of the community is under the age of 35?
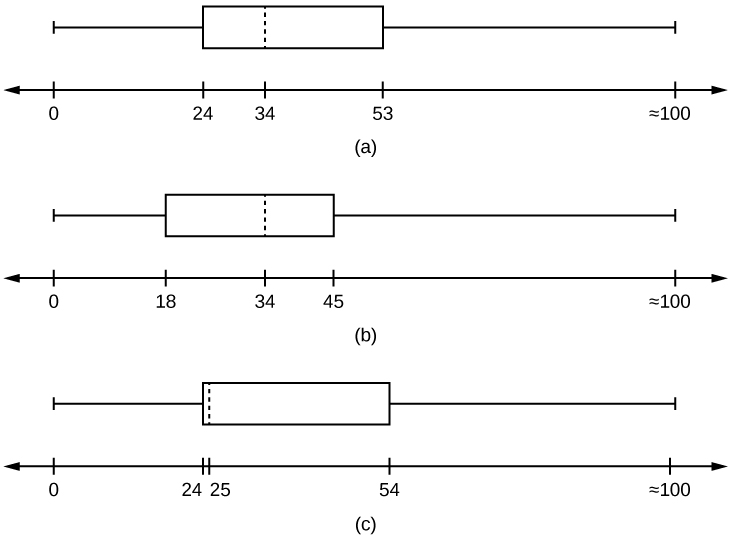
- Which box plot most resembles the information above?
12. For the following 13 real estate prices, calculate the IQR and determine if any prices are potential outliers. Prices are in dollars.
Data: 389,950; 230,500; 158,000; 479,000; 639,000; 114,950; 5,500,000; 387,000; 659,000; 529,000; 575,000; 488,800; 1,095,000
13. For the following 11 salaries, calculate the IQR and determine if any salaries are outliers. The salaries are in dollars.
$33,000, $64,500, $28,000, $54,000, $72,000, $68,500, $69,000, $42,000, $54,000, $120,000, $40,500
14. For the two datasets about test scores in the first question of this section, find the following:
- Both interquartile ranges. Compare the two.
- Any outliers in either set.
15. Find the interquartile range for the following two datasets and compare them.
Test Scores for Class A:
69, 96, 81, 79, 65, 76, 83, 99, 89, 67, 90, 77, 85, 98, 66, 91, 77, 69, 80, 94
Test Scores for Class B:
90, 72, 80, 92, 90, 97, 92, 75, 79, 68, 70, 80, 99, 95, 78, 73, 71, 68, 95, 100
16. Fifty statistics students were asked how much sleep they get per school night (rounded to the nearest hour). The results were:
| Amount of sleep per school night (hours) | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 4 | 2 | 0.04 | 0.04 |
| 5 | 5 | 0.10 | 0.14 |
| 6 | 7 | 0.14 | 0.28 |
| 7 | 12 | 0.24 | 0.52 |
| 8 | 14 | 0.28 | 0.80 |
| 9 | 7 | 0.14 | 0.94 |
| 10 | 3 | 0.06 | 1.00 |
Figure 2.80
- Find the 28th percentile.
- Find the median.
- Find the third quartile.
17. Forty bus drivers were asked how many hours they spend each day running their routes (rounded to the nearest hour). Find the 65th percentile.
| Amount of time spent on route (hours) | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 2 | 12 | 0.30 | 0.30 |
| 3 | 14 | 0.35 | 0.65 |
| 4 | 10 | 0.25 | 0.90 |
| 5 | 4 | 0.10 | 1.00 |
Figure 2.81
18. Using the table below:
| Amount of sleep per school night (hours) | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 4 | 2 | 0.04 | 0.04 |
| 5 | 5 | 0.10 | 0.14 |
| 6 | 7 | 0.14 | 0.28 |
| 7 | 12 | 0.24 | 0.52 |
| 8 | 14 | 0.28 | 0.80 |
| 9 | 7 | 0.14 | 0.94 |
| 10 | 3 | 0.06 | 1.00 |
Figure 2.82
- Find the 80th percentile.
- Find the 90th percentile.
- Find the first quartile. What is another name for the first quartile?
19. Refer to the table below. Find the third quartile. What is another name for the third quartile?
| Amount of time spent on route (hours) | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 2 | 12 | 0.30 | 0.30 |
| 3 | 14 | 0.35 | 0.65 |
| 4 | 10 | 0.25 | 0.90 |
| 5 | 4 | 0.10 | 1.00 |
Figure 2.83
20. Twenty-nine ages of winners of the Academy Award for Best Actor are listed below in order from smallest to largest.
18, 21, 22, 25, 26, 27, 29, 30, 31, 33, 36, 37, 41, 42, 47, 52, 55, 57, 58, 62, 64, 67, 69, 71, 72, 73, 74, 76, 77
- Find the 40th percentile.
- Find the 78th percentile.
21. Twenty-nine ages of winners of the Academy Award for Best Actor are listed below in order from smallest to largest.
18, 18, 21, 22, 25, 26, 27, 29, 30, 31, 31, 33, 36, 37, 37, 41, 42, 47, 52, 55, 57, 58, 62, 64, 67, 69, 71, 72, 73, 74, 76, 77
- Find the percentile of 37.
- Find the percentile of 72.
22. Jesse was ranked 37th in his graduating class of 180 students. At what percentile is Jesse’s ranking?
23. For runners in a race, a low time means a faster run. The winners in a race have the shortest running times.
- Is it more desirable to have a finish time with a high or a low percentile when running a race?
- The 20th percentile of run times in a particular race is 5.2 minutes. Write a sentence interpreting the 20th percentile in the context of the situation.
- A bicyclist in the 90th percentile of a bicycle race completed the race in 1 hour and 12 minutes. Is he among the fastest or slowest cyclists in the race? Write a sentence interpreting the 90th percentile in the context of the situation.
24. For runners in a race, a higher speed means a faster run.
- Is it more desirable to have a speed with a high or a low percentile when running a race?
- The 40th percentile of speeds in a particular race is 7.5 miles per hour. Write a sentence interpreting the 40th percentile in the context of the situation.
25. On an exam, would it be more desirable to earn a grade with a high or low percentile? Explain.
26. Mina is waiting in line at the Department of Motor Vehicles (DMV). Her wait time of 32 minutes is the 85th percentile of wait times. Is that good or bad? Write a sentence interpreting the 85th percentile in the context of this situation.
27. In a survey collecting data about the salaries earned by recent college graduates, Li found that her salary was in the 78th percentile. Should Li be pleased or upset by this result? Explain.
28. In a study collecting data about the repair costs of damage to automobiles in a certain type of crash tests, a certain model of car sustained $1,700 in damage and was in the 90th percentile. Should the manufacturer and the consumer be pleased or upset by this result? Explain, and write a one-sentence interpretation of the 90th percentile in the context of this problem.
29. The University of California has two criteria used to set admission standards for freshman to be admitted to a college in the UC system:
- Students’ GPAs and scores on standardized tests (SATs and ACTs) are entered into a formula that calculates an “admissions index” score. The admissions index score is used to set eligibility standards intended to meet the goal of admitting the top 12% of high school students in the state. In this context, what percentile does the top 12% represent?
- Students whose GPAs are at or above the 96th percentile of all students at their high school are eligible (called “eligible in the local context”), even if they are not in the top 12% of all students in the state. What percentage of students from each high school are eligible in the local context?
30. Suppose that you are buying a house. You and your realtor have determined that the most expensive house you can afford is in the 34th percentile. The 34th percentile of housing prices is $240,000 in the town to which you want to move. In this town, can you afford 34% of the houses or 66% of the houses?
31. Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. 14 people answered that they generally sell three cars, 19 generally sell four cars, 12 generally sell five cars, 9 generally sell six cars, and 11 generally sell seven cars. Identify the following:
- First quartile
- Second quartile = median = 50th percentile
- Third quartile
- Interquartile range (IQR)
- 10th percentile
- 70th percentile
32. The median age for Black US citizens is 30.9 years; for White US citizens, it is 42.3 years.
- Based upon this information, give two reasons why the Black median age could be lower than the White median age.
- Does the lower median age for Black citizens necessarily mean that Black citizens die younger than White citizens? Why or why not?
- How might it be possible for Black and White citizens to die at approximately the same age, even though the median age for White citizens is higher?
33. Six hundred adult Americans were asked by telephone poll, “What do you think constitutes a middle-class income?” The results are in the figure below.
| Salary ($) | Relative frequency |
|---|---|
| < 20,000 | 0.02 |
| 20,000–25,000 | 0.09 |
| 25,000–30,000 | 0.19 |
| 30,000–40,000 | 0.26 |
| 40,000–50,000 | 0.18 |
| 50,000–75,000 | 0.17 |
| 75,000–99,999 | 0.02 |
| 100,000+ | 0.01 |
Figure 2.84
- What percentage of the survey answered “not sure”?
- What percentage think that middle-class is from $25,000 to $50,000?
- Construct a histogram of the data. Include left endpoint, but not the right endpoint.
- Should all bars have the same width, based on the data? Why or why not?
- How should the < 20,000 and the 100,000+ intervals be handled? Why?
- Find the 40th and 80th percentiles.
- Construct a bar graph of the data.
34. Given the following box plot:

- Which quarter has the smallest spread of data? What is that spread?
- Which quarter has the largest spread of data? What is that spread?
- Find the interquartile range (IQR).
- Are there more data in the 5-10 interval or in the 10-13 interval? How do you know this?
- Which interval has the fewest data in it? How do you know this?
- 0–2
- 2–4
- 10–12
- 12–13
- need more information
35. The following box plot shows the US population for 1990.
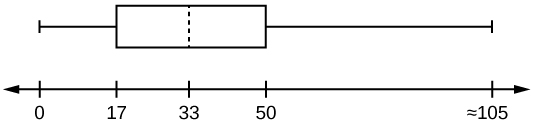
- Are there fewer or more children (age 17 and under) than senior citizens (age 65 and over)? How do you know?
- Of the population, 12.6% are age 65 and over. Approximately what percentage of the population are working age adults between the ages of 17 and 65?
36. On a 20-question math test, the 70th percentile for number of correct answers was 16. Interpret the 70th percentile in the context of this situation.
37. On a 60-point written assignment, the 80th percentile for the number of points earned was 49. Interpret the 80th percentile in the context of this situation.
38. At a community college, it was found that the 30th percentile of number of credit units for which students are enrolled is seven units. Interpret the 30th percentile in the context of this situation.
39. During a season, the 40th percentile for points scored per player in a game is eight. Interpret the 40th percentile in the context of this situation.
40. Thirty people spent two weeks around Mardi Gras in New Orleans. Their two-week weight gain is below. Note that a loss is shown by a negative weight gain.
| Weight gain | Frequency |
|---|---|
| -2 | 3 |
| -1 | 5 |
| 0 | 2 |
| 1 | 4 |
| 4 | 13 |
| 6 | 2 |
| 11 | 1 |
Figure 2.87
- Calculate the following values:
- the average weight gain for the two weeks
- the standard deviation
- the first, second, and third quartiles
- Construct a histogram and box plot of the data.
41. The figure below shows the amount, in inches, of annual rainfall in a sample of towns.
| Rainfall (Inches) | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 2.95–4.97 | 6 | 0.12 | |
| 4.97–6.99 | 7 | 0.12 + 0.14 = 0.26 | |
| 6.99–9.01 | 15 | 0.26 + 0.30 = 0.56 | |
| 9.01–11.03 | 8 | 0.56 + 0.16 = 0.72 | |
| 11.03–13.05 | 9 | 0.72 + 0.18 = 0.90 | |
| 13.05–15.07 | 5 | 0.90 + 0.10 = 1.00 | |
| Total = 50 | Total = 1.00 |
Figure 2.88
a. From the figure above, find the percentage of rainfall that is less than 9.01 inches.
b. Find the percentage of rainfall that is between 6.99 and 13.05 inches.
c. Find the number of towns that have rainfall between 2.95 and 9.01 inches.
d. What fraction of towns surveyed get between 11.03 and 13.05 inches of rainfall each year?
42. Nineteen people were asked how many miles, to the nearest mile, they commute to work each day. The data are as follows: 2, 5, 7, 3, 2, 10, 18, 15, 20, 7, 10, 18, 5, 12, 13, 12, 4, 5, 10. The following table was produced:
| Data | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 3 | 3 | 0.1579 | |
| 4 | 1 | 0.2105 | |
| 5 | 3 | 0.1579 | |
| 7 | 2 | 0.2632 | |
| 10 | 3 | 0.4737 | |
| 12 | 2 | 0.7895 | |
| 13 | 1 | 0.8421 | |
| 15 | 1 | 0.8948 | |
| 18 | 1 | 0.9474 | |
| 20 | 1 | 1.0000 |
Figure 2.89
- Is the table correct? If it is not correct, what is wrong?
- True or False: Three percent of the people surveyed commute three miles. If the statement is not correct, what should it be? If the table is incorrect, make the corrections.
- What fraction of the people surveyed commute five or seven miles?
- What fraction of the people surveyed commute 12 miles or more? Fewer than 12 miles? Between five and 13 miles (not including five and 13 miles)?
43. Sixty adults with gum disease were asked the number of times per week they used to floss before being diagnosed. The (incomplete) results are shown in the figure below:
| Times flossing per week | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 0 | 27 | 0.4500 | |
| 1 | 18 | ||
| 3 | 0.9333 | ||
| 6 | 3 | 0.0500 | |
| 7 | 1 | 0.0167 |
Figure 2.90
- Fill in the blanks in the figure above.
- What percent of adults flossed six times per week?
- What percent flossed at most three times per week?
44. Nineteen immigrants to the US were asked how many years, to the nearest year, they have lived in the US. The data are as follows: 2, 5, 7, 2, 2, 10, 20, 15, 0, 7, 0, 20, 5, 12, 15, 12, 4, 5, 10.
| Data | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 0 | 2 | 0.1053 | |
| 2 | 3 | 0.2632 | |
| 4 | 1 | 0.3158 | |
| 5 | 3 | 0.4737 | |
| 7 | 2 | 0.5789 | |
| 10 | 2 | 0.6842 | |
| 12 | 2 | 0.7895 | |
| 15 | 1 | 0.8421 | |
| 20 | 1 | 1.0000 |
Figure 2.91
- Fix the errors in the figure above. In addition, explain how someone might have arrived at the incorrect number(s).
- Explain what is wrong with this statement: “47 percent of the people surveyed have lived in the US for 5 years.”
- Fix the statement in b. to make it correct.
- What fraction of the people surveyed have lived in the US five or seven years?
- What fraction of the people surveyed have lived in the US at most 12 years?
- What fraction of the people surveyed have lived in the US fewer than 12 years?
- What fraction of the people surveyed have lived in the US from five to 20 years, inclusive?
45. The population in Park City is made up of children, working-age adults, and retirees. The figure below shows the three age groups, the number of people in the town from each age group, and the proportion (%) of people in each age group. Construct a bar graph showing the proportions.
| Age groups | Number of people | Proportion of population |
|---|---|---|
| Children | 67,059 | 19% |
| Working-age adults | 152,198 | 43% |
| Retirees | 131,662 | 38% |
Figure 2.92
46. The following data are the distances (in kilometers) from a home to local supermarkets:
1.1, 1.5, 2.3, 2.5, 2.7, 3.2, 3.3, 3.3, 3.5, 3.8, 4.0, 4.2, 4.5, 4.5, 4.7, 4.8, 5.5, 5.6, 6.5, 6.7, 12.3
- Create a stemplot using the data.
- Do the data seem to have any concentration of values?
47. The following data show the distances (in miles) from the homes of off-campus statistics students to the college:
0.5, 0.7, 1.1, 1.2, 1.2, 1.3, 1.3, 1.5, 1.5, 1.7, 1.7, 1.8, 1.9, 2.0, 2.2, 2.5, 2.6, 2.8, 2.8, 2.8, 3.5, 3.8, 4.4, 4.8, 4.9, 5.2, 5.5, 5.7, 5.8, 8.0
Create a stem plot using the data, and identify any outliers.
48. For the Park City basketball team, scores for the last 30 games were as follows (smallest to largest):
32, 32, 33, 34, 38, 40, 42, 42, 43, 44, 46, 47, 47, 48, 48, 48, 49, 50, 50, 51, 52, 52, 52, 53, 54, 56, 57, 57, 60, 61
Construct a stem plot for the data.
49. The table below shows the number of wins and losses the Atlanta Hawks have had in 42 seasons. Create a side-by-side stem-and-leaf plot of these wins and losses.
| Losses | Wins | Year | Losses | Wins | Year |
|---|---|---|---|---|---|
| 34 | 48 | 1968–1969 | 41 | 41 | 1989–1990 |
| 34 | 48 | 1969-1970 | 39 | 43 | 1990–1991 |
| 46 | 36 | 1970-1971 | 44 | 38 | 1991–1992 |
| 46 | 36 | 1971-1972 | 39 | 43 | 1992–1993 |
| 36 | 46 | 1972-1973 | 25 | 57 | 1993–1994 |
| 47 | 35 | 1973-1974 | 40 | 42 | 1994–1995 |
| 51 | 31 | 1974-1975 | 36 | 46 | 1995–1996 |
| 53 | 29 | 1975-1976 | 26 | 56 | 1996–1997 |
| 51 | 31 | 1976-1977 | 32 | 50 | 1997–1998 |
| 41 | 41 | 1977-1978 | 19 | 31 | 1998–1999 |
| 36 | 46 | 1978-1979 | 54 | 28 | 1999–2000 |
| 32 | 50 | 1979-1980 | 57 | 25 | 2000–2001 |
| 51 | 31 | 1980-1981 | 49 | 33 | 2001–2002 |
| 40 | 42 | 1981-1982 | 47 | 35 | 2002–2003 |
| 39 | 43 | 1982-1983 | 54 | 28 | 2003–2004 |
| 42 | 40 | 1983-1984 | 69 | 13 | 2004–2005 |
| 48 | 34 | 1984-1985 | 56 | 26 | 2005–2006 |
| 32 | 50 | 1985-1986 | 52 | 30 | 2006–2007 |
| 25 | 57 | 1986-1987 | 45 | 37 | 2007–2008 |
| 32 | 50 | 1987-1988 | 35 | 47 | 2008–2009 |
| 30 | 52 | 1988-1989 | 29 | 53 | 2009–2010 |
Figure 2.93
50. In a survey, 40 people were asked how many times per year their car was in the shop for repairs. The results are shown in the table below. Construct a line graph.
| Number of times in shop | Frequency |
|---|---|
| 0 | 7 |
| 1 | 10 |
| 2 | 14 |
| 3 | 9 |
Figure 2.94
51. Using the following dataset, construct a histogram.
| Number of hours my classmates spent playing video games on weekends | ||||
|---|---|---|---|---|
| 9.95 | 10 | 2.25 | 16.75 | 0 |
| 19.5 | 22.5 | 7.5 | 15 | 12.75 |
| 5.5 | 11 | 10 | 20.75 | 17.5 |
| 23 | 21.9 | 24 | 23.75 | 18 |
| 20 | 15 | 22.9 | 18.8 | 20.5 |
Figure 2.95
52. The following data represent the number of employees at various restaurants in New York City:
22, 35, 15, 26, 40, 28, 18, 20, 25, 34, 39, 42, 24, 22, 19, 27, 22, 34, 40, 20, 38, 28
Using this data, create a histogram. Use 10–19 as the first interval.
53. Suppose 111 people who shopped in a special T-shirt store were asked the number of T-shirts they own that cost more than $19 each.
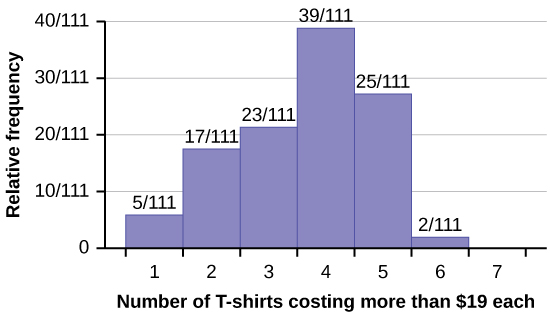
a. The percentage of people who own at most three t-shirts costing more than $19 each is approximately:
- 21
- 59
- 41
- Cannot be determined
b. If the data were collected by asking the first 111 people who entered the store, then the type of sampling is:
- cluster
- simple random
- stratified
- convenience
54. Following are the 2010 obesity rates of the US states and Washington, DC.[8]
| State | Percent (%) | State | Percent (%) | State | Percent (%) |
|---|---|---|---|---|---|
| Alabama | 32.2 | Kentucky | 31.3 | North Dakota | 27.2 |
| Alaska | 24.5 | Louisiana | 31.0 | Ohio | 29.2 |
| Arizona | 24.3 | Maine | 26.8 | Oklahoma | 30.4 |
| Arkansas | 30.1 | Maryland | 27.1 | Oregon | 26.8 |
| California | 24.0 | Massachusetts | 23.0 | Pennsylvania | 28.6 |
| Colorado | 21.0 | Michigan | 30.9 | Rhode Island | 25.5 |
| Connecticut | 22.5 | Minnesota | 24.8 | South Carolina | 31.5 |
| Delaware | 28.0 | Mississippi | 34.0 | South Dakota | 27.3 |
| Washington, DC | 22.2 | Missouri | 30.5 | Tennessee | 30.8 |
| Florida | 26.6 | Montana | 23.0 | Texas | 31.0 |
| Georgia | 29.6 | Nebraska | 26.9 | Utah | 22.5 |
| Hawaii | 22.7 | Nevada | 22.4 | Vermont | 23.2 |
| Idaho | 26.5 | New Hampshire | 25.0 | Virginia | 26.0 |
| Illinois | 28.2 | New Jersey | 23.8 | Washington | 25.5 |
| Indiana | 29.6 | New Mexico | 25.1 | West Virginia | 32.5 |
| Iowa | 28.4 | New York | 23.9 | Wisconsin | 26.3 |
| Kansas | 29.4 | North Carolina | 27.8 | Wyoming | 25.1 |
Figure 2.97
Construct a bar graph of obesity rates of your state and the four states closest to your state, labeling the x-axis with the states. Answers will vary.
55. Student grades on a chemistry exam were 77, 78, 76, 81, 86, 51, 79, 82, 84, and 99.
- Construct a stem-and-leaf plot of the data.
- Are there any potential outliers? If so, which scores are they? Why do you consider them outliers?
56. The table below contains the 2010 obesity rates of US states and Washington, DC.[9]
| State | Percent (%) | State | Percent (%) | State | Percent (%) |
|---|---|---|---|---|---|
| Alabama | 32.2 | Kentucky | 31.3 | North Dakota | 27.2 |
| Alaska | 24.5 | Louisiana | 31.0 | Ohio | 29.2 |
| Arizona | 24.3 | Maine | 26.8 | Oklahoma | 30.4 |
| Arkansas | 30.1 | Maryland | 27.1 | Oregon | 26.8 |
| California | 24.0 | Massachusetts | 23.0 | Pennsylvania | 28.6 |
| Colorado | 21.0 | Michigan | 30.9 | Rhode Island | 25.5 |
| Connecticut | 22.5 | Minnesota | 24.8 | South Carolina | 31.5 |
| Delaware | 28.0 | Mississippi | 34.0 | South Dakota | 27.3 |
| Washington, DC | 22.2 | Missouri | 30.5 | Tennessee | 30.8 |
| Florida | 26.6 | Montana | 23.0 | Texas | 31.0 |
| Georgia | 29.6 | Nebraska | 26.9 | Utah | 22.5 |
| Hawaii | 22.7 | Nevada | 22.4 | Vermont | 23.2 |
| Idaho | 26.5 | New Hampshire | 25.0 | Virginia | 26.0 |
| Illinois | 28.2 | New Jersey | 23.8 | Washington | 25.5 |
| Indiana | 29.6 | New Mexico | 25.1 | West Virginia | 32.5 |
| Iowa | 28.4 | New York | 23.9 | Wisconsin | 26.3 |
| Kansas | 29.4 | North Carolina | 27.8 | Wyoming | 25.1 |
Figure 2.98
- Use a random number generator to randomly pick eight states. Construct a bar graph of the obesity rates of those eight states.
- Construct a bar graph for all the states beginning with the letter “A.”
- Construct a bar graph for all the states beginning with the letter “M.”
57. For each of the following datasets, create a stem plot and identify any outliers.
- The miles per gallon rating for 30 cars are shown below (lowest to highest).
19, 19, 19, 20, 21, 21, 25, 25, 25, 26, 26, 28, 29, 31, 31, 32, 32, 33, 34, 35, 36, 37, 37, 38, 38, 38, 38, 41, 43, 43 - The height (in feet) of 25 trees is shown below (lowest to highest).
25, 27, 33, 34, 34, 34, 35, 37, 37, 38, 39, 39, 39, 40, 41, 45, 46, 47, 49, 50, 50, 53, 53, 54, 54 - The data are the prices of different laptops at an electronics store. Round each value to the nearest ten.
249, 249, 260, 265, 265, 280, 299, 299, 309, 319, 325, 326, 350, 350, 350, 365, 369, 389, 409, 459, 489, 559, 569, 570, 610 - The data are daily high temperatures in a town for one month.
61, 61, 62, 64, 66, 67, 67, 67, 68, 69, 70, 70, 70, 71, 71, 72, 74, 74, 74, 75, 75, 75, 76, 76, 77, 78, 78, 79, 79, 95
58. The students in Ms. Ramirez’s math class have birthdays in each of the four seasons. The figure below shows the four seasons, the number of students who have birthdays in each season, and the percentage (%) of students in each group. Construct a bar graph showing the number of students.
| Seasons | Number of students | Proportion of population |
|---|---|---|
| Spring | 8 | 24% |
| Summer | 9 | 26% |
| Autumn | 11 | 32% |
| Winter | 6 | 18% |
Figure 2.99
Using the data from Ms. Ramirez’s math class, construct a bar graph showing the percentages.
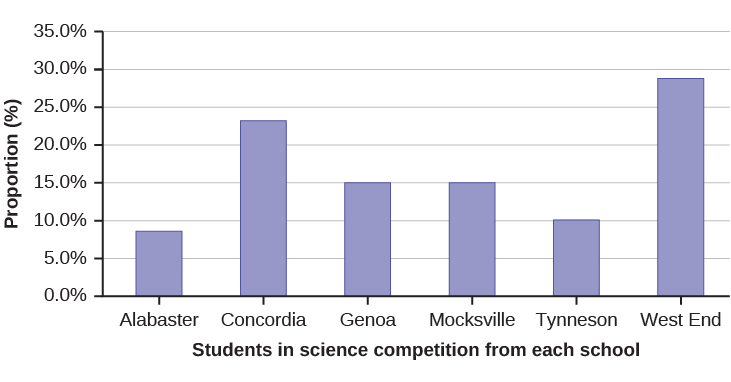
59. David County has six high schools. Each school sent students to participate in a county-wide science competition. The figure below shows the percentage breakdown of competitors from each school and the percentage of the entire student population of the county that goes to each school. Construct a bar graph that shows the population percentage of competitors from each school.
| High school | Science competition population | Overall student population |
|---|---|---|
| Alabaster | 28.9% | 8.6% |
| Concordia | 7.6% | 23.2% |
| Genoa | 12.1% | 15.0% |
| Mocksville | 18.5% | 14.3% |
| Tynneson | 24.2% | 10.1% |
| West End | 8.7% | 28.8% |
Figure 2.100
Use the data from the David County science competition supplied above to construct a bar graph that shows the county-wide population percentage of students at each school.
2.6 Measures of Center
1. The following data show the number of months patients typically wait on a transplant list before getting surgery. The data are ordered from smallest to largest. Calculate the mean and median.
3, 4, 5, 7, 7, 7, 7, 8, 8, 9, 9, 10, 10, 10, 10, 10, 11, 12, 12, 13, 14, 14, 15, 15, 17, 17, 18, 19, 19, 19, 21, 21, 22, 22, 23, 24, 24, 24, 24
2. In a sample of 60 households, one house is worth $2,500,000. Half of the rest are worth $280,000, and all the others are worth $315,000. Which is the better measure of the “center,” the mean or the median?
3. The number of books checked out from the library from 25 students are as follows:
0, 0, 0, 1, 2, 3, 3, 4, 4, 5, 5, 7, 7, 7, 7, 8, 8, 8, 9, 10, 10, 11, 11, 12, 12
Find the mode.
4. Find the mean for the following frequency tables.
-
Grade Frequency 49.5–59.5 2 59.5–69.5 3 69.5–79.5 8 79.5–89.5 12 89.5–99.5 5 Figure 2.102
-
Daily low temperature Frequency 49.5–59.5 53 59.5–69.5 32 69.5–79.5 15 79.5–89.5 1 89.5–99.5 0 Figure 2.103
-
Points per game Frequency 49.5–59.5 14 59.5–69.5 32 69.5–79.5 15 79.5–89.5 23 89.5–99.5 2 Figure 2.104
5. The following data show the lengths of boats moored in a marina. The data are ordered from smallest to largest: 16, 17, 19, 20, 20, 21, 23, 24, 25, 25, 25, 26, 26, 27, 27, 27, 28, 29, 30, 32, 33, 33, 34, 35, 37, 39, 40
- Calculate the mean.
- Identify the median.
- Identify the mode.
6. Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. 14 people answered that they generally sell three cars, 19 generally sell four cars, 12 generally sell five cars, 9 generally sell six cars, and 11 generally sell seven cars. Calculate the following:
- Calculate the sample mean.
- Identify the median.
- Identify the mode.
7. The most obese countries in the world have obesity rates that range from 11.4% to 74.6%. This data is summarized in the following table.[10]
| Percent of population obese | Number of countries |
|---|---|
| 11.4–20.45 | 29 |
| 20.45–29.45 | 13 |
| 29.45–38.45 | 4 |
| 38.45–47.45 | 0 |
| 47.45–56.45 | 2 |
| 56.45–65.45 | 1 |
| 65.45–74.45 | 0 |
| 74.45–83.45 | 1 |
Figure 2.105
- What is the best estimate of the average obesity percentage for these countries?
- The United States has an average obesity rate of 33.9%. Is this rate above average or below?
- How does the United States compare to other countries?
8. The following figure gives the percent of children under five considered to be underweight. What is the best estimate for the mean percentage of underweight children?[11]
| Percent of children underweight | Number of countries |
|---|---|
| 16–21.45 | 23 |
| 21.45–26.9 | 4 |
| 26.9–32.35 | 9 |
| 32.35–37.8 | 7 |
| 37.8–43.25 | 6 |
| 43.25–48.7 | 1 |
Figure 2.106
The mean percentage, ![]() =
= ![]() = 26.75
= 26.75
9. Discuss the mean, median, and mode for each of the following problems. Is there a pattern between the shape and measure of the center?
-

Figure 2.107. Figure description available at the end of the section. -
The ages former US presidents died 4 6 9 5 3 6 7 7 7 8 6 0 0 3 3 4 4 5 6 7 7 7 8 7 0 1 1 2 3 4 7 8 8 9 8 0 1 3 5 8 9 0 0 3 3 Key: 8|0 means 80. Figure 2.108
10. State whether the data are symmetrical, skewed to the left, or skewed to the right.
- 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 5
- 16, 17, 19, 22, 22, 22, 22, 22, 23
- 87, 87, 87, 87, 87, 88, 89, 89, 90, 91
11. When the data are skewed left, what is the typical relationship between the mean and median?
12. When the data are symmetrical, what is the typical relationship between the mean and median?
13. What word describes a distribution that has two modes?
14. Use the following graph to answer a.-c.
- Describe the shape of this distribution.
- Describe the relationship between the mode and the median of this distribution.
- Describe the relationship between the mean and the median of this distribution.
15. Data: 11, 11, 12, 12, 12, 12, 13, 15, 17, 22, 22, 22
- Is the data perfectly symmetrical? Why or why not?
- Which is the largest, the mean, the mode, or the median of the dataset?
16. Data: 56, 56, 56, 58, 59, 60, 62, 64, 64, 65, 67
- Is the data perfectly symmetrical? Why or why not?
- Which is the largest, the mean, the mode, or the median of the dataset?
17. Of the three measures, which tends to reflect skewing the most, the mean, the mode, or the median? Why?
18. In a perfectly symmetrical distribution, when would the mode be different from the mean and median?
19. The median age of the US population in 1980 was 30.0 years. In 1991, the median age was 33.1 years.
- What does it mean for the median age to rise?
- Give two reasons why the median age could rise.
- Does the median age rising mean the actual age of children in 1991 was less than in 1980? Why or why not?
20. Javier and Ercilia are supervisors at a shopping mall. Each was given the task of estimating the mean distance that shoppers live from the mall. They each randomly surveyed 100 shoppers. The samples yielded the following information.
| Javier | Ercilia | |
|---|---|---|
| 6.0 miles | 6.0 miles | |
| 4.0 miles | 7.0 miles |
Figure 2.111
- How can you determine which survey was correct?
- Explain what the difference in the results of the surveys implies about the data.
- If the following two histograms depict the distribution of values for each supervisor, which one depicts Ercilia’s sample? How do you know?
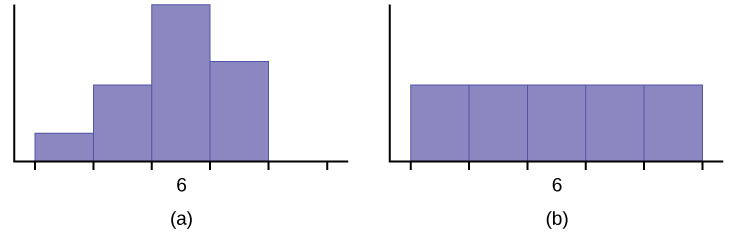
Figure 2.112. Figure description available at the end of the section. - If the two box plots depict the distribution of values for each supervisor, which one depicts Ercilia’s sample? How do you know?
21. We are interested in the number of years students in a particular elementary statistics class have lived in California. The information in the following table is from the entire section.
| Number of years | Frequency |
|---|---|
| 7 | 1 |
| 14 | 3 |
| 15 | 1 |
| 18 | 1 |
| 19 | 4 |
| 20 | 3 |
| 22 | 1 |
| 23 | 1 |
| 26 | 1 |
| 40 | 2 |
| 42 | 2 |
| Total = 20 |
Figure 2.114
What is the IQR?
- 11
- 35
- 15
- 8
What is the mode?
- 19
- 19.5
- 14 and 20
- 22.65
Is this a sample or the entire population?
- sample
- entire population
- neither
22. How much time does it take to travel to work? The figure below shows the mean commute time by state for workers at least 16 years old who are not working at home. Find the mean travel time, and round off the answer properly.
| Mean commute times (by state) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 24.0 | 24.3 | 25.9 | 18.9 | 27.5 | 17.9 | 21.8 | 20.9 | 16.7 | 27.3 |
| 18.2 | 24.7 | 20.0 | 22.6 | 23.9 | 18.0 | 31.4 | 22.3 | 24.0 | 25.5 |
| 24.7 | 24.6 | 28.1 | 24.9 | 22.6 | 23.6 | 23.4 | 25.7 | 24.8 | 25.5 |
| 21.2 | 25.7 | 23.1 | 23.0 | 23.9 | 26.0 | 16.3 | 23.1 | 21.4 | 21.5 |
| 27.0 | 27.0 | 18.6 | 31.7 | 23.3 | 30.1 | 22.9 | 23.3 | 21.7 | 18.6 |
Figure 2.115
23. Find the midpoint for each class. These will be graphed on the x-axis. The frequency values will be graphed on the y-axis values.
2.7 Measures of Spread
1. Use the following data (first exam scores) from Susan Dean’s spring pre-calculus class:
33, 42, 49, 49, 53, 55, 55, 61, 63, 67, 68, 68, 69, 69, 72, 73, 74, 78, 80, 83, 88, 88, 88, 90, 92, 94, 94, 94, 94, 96, 100
- Create a chart containing the data, frequencies, relative frequencies, and cumulative relative frequencies to three decimal places.
- Calculate the following to one decimal place:
- The sample mean
- The sample standard deviation
- The median
- The first quartile
- The third quartile
- IQR
- Construct a box plot and a histogram on the same set of axes. Make comments about the box plot, the histogram, and the chart.
2. The following data show the different types of pet food that stores in the area carry:
6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 9, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12
Calculate the sample mean and the sample standard deviation to one decimal place.
3. The following data are the distances (in miles) between 20 retail stores and a large distribution center:
29, 37, 38, 40, 58, 67, 68, 69, 76, 86, 87, 95, 96, 96, 99, 106, 112, 127, 145, 150
- Use a graphing calculator or computer to find the standard deviation and round to the nearest tenth.
- Find the value that is one standard deviation below the mean.
4. Fredo and Karl, two baseball players on different teams, wanted to find out who had the higher batting average when compared to his team. Which baseball player had the higher batting average when compared to his team?
| Baseball player | Batting average | Team batting average | Team standard deviation |
|---|---|---|---|
| Fredo | 0.158 | 0.166 | 0.012 |
| Karl | 0.177 | 0.189 | 0.015 |
Figure 2.117
For Fredo:
z = ![]() = –0.67
= –0.67
For Karl:
z = ![]() = –0.8
= –0.8
Fredo’s z-score of –0.67 is higher than Karl’s z-score of –0.8. For batting average, higher values are better, so Fredo has a better batting average compared to his team.
Use the table above to find the value that is three standard deviations (a) above the mean and (b) below the mean.
5. Find the standard deviation for the following frequency tables using the formula. Check the calculations with the TI 83/84.
| Grade | Frequency |
|---|---|
| 49.5–59.5 | 2 |
| 59.5–69.5 | 3 |
| 69.5–79.5 | 8 |
| 79.5–89.5 | 12 |
| 89.5–99.5 | 5 |
Figure 2.118
| Daily low temperature | Frequency |
|---|---|
| 49.5–59.5 | 53 |
| 59.5–69.5 | 32 |
| 69.5–79.5 | 15 |
| 79.5–89.5 | 1 |
| 89.5–99.5 | 0 |
Figure 2.119
| Points per game | Frequency |
|---|---|
| 49.5–59.5 | 14 |
| 59.5–69.5 | 32 |
| 69.5–79.5 | 15 |
| 79.5–89.5 | 23 |
| 89.5–99.5 | 2 |
Figure 2.120
6. The population parameters below describe the number of full-time equivalent students (FTES) each year at ABC University from 1976–1977 through 2004–2005.
μ = 1,000 FTES
Median = 1,014 FTES
σ = 474 FTES
First quartile = 528.5 FTES
Third quartile = 1,447.5 FTES
n = 29 years
- A sample of 11 years is taken. About how many are expected to have a FTES of 1,014 or above? Explain how you determined your answer.
- 75% of all years have an FTES:
- At or below:
- At or above:
- What is the population standard deviation?
- What percent of the FTES were from 528.5 to 1447.5? How do you know?
- What is the IQR? What does the IQR represent?
- How many standard deviations away from the mean is the median? Additional Information: The population FTES for 2005–2006 through 2010–2011 was given in an updated report. The data are reported here:
FTES population Year 2005-06 2006–07 2007–08 2008–09 2009–10 2010–11 Total FTFS 1,585 1,690 1,735 1,935 2,021 1,890 Figure 2.121
- Calculate the mean, median, standard deviation, the first quartile, the third quartile and the IQR. Round to one decimal place.
- What additional information is needed to construct a box plot for the FTES for 2005-2006 through 2010-2011 and a box plot for the FTES for 1976-1977 through 2004-2005?
- Compare the IQR for the FTES for 1976–77 through 2004–2005 with the IQR for the FTES for 2005-2006 through 2010–2011. Why do you suppose the IQRs are so different? Hint: Think about the number of years covered by each time period and what happened to higher education during those periods.
7. Three students are applying to the same graduate school. They come from schools with different grading systems. Which student had the best GPA when compared to other students at his school? Explain how you determined your answer.
| Student | GPA | School average GPA | School standard deviation |
|---|---|---|---|
| Thuy | 2.7 | 3.2 | 0.8 |
| Vichet | 87 | 75 | 20 |
| Kamala | 8.6 | 8 | 0.4 |
Figure 2.122
8. A music school has budgeted to purchase three musical instruments. They plan to purchase a piano costing $3,000, a guitar costing $550, and a drum set costing $600. The mean cost for a piano is $4,000 with a standard deviation of $2,500. The mean cost for a guitar is $500 with a standard deviation of $200. The mean cost for drums is $700 with a standard deviation of $100. Which cost is the lowest when compared to other instruments of the same type? Which cost is the highest when compared to other instruments of the same type? Justify your answer.
9. An elementary school class ran one mile with a mean of 11 minutes and a standard deviation of three minutes. Rachel, a student in the class, ran one mile in eight minutes. A junior high school class ran one mile with a mean of nine minutes and a standard deviation of two minutes. Kenji, a student in the class, ran one mile in 8.5 minutes. A high school class ran one mile with a mean of seven minutes and a standard deviation of four minutes. Nedda, a student in the class, ran one mile in eight minutes.
- Why is Kenji considered a better runner than Nedda, even though Nedda ran faster than he?
- Who is the fastest runner with respect to their class? Explain why.
10. The most obese countries in the world have obesity rates that range from 11.4% to 74.6%. This data is summarized in figure 2.123.[12]
| Percent of population obese | Number of countries |
|---|---|
| 11.4–20.45 | 29 |
| 20.45–29.45 | 13 |
| 29.45–38.45 | 4 |
| 38.45–47.45 | 0 |
| 47.45–56.45 | 2 |
| 56.45–65.45 | 1 |
| 65.45–74.45 | 0 |
| 74.45–83.45 | 1 |
Figure 2.123
- What is the best estimate of the average obesity percentage for these countries?
- What is the standard deviation for the listed obesity rates?
- The United States has an average obesity rate of 33.9%. Is this rate above average or below?
- How “unusual” is the United States’ obesity rate compared to the average rate? Explain.
11. The figure below gives the percent of children under five considered to be underweight.[13]
| Percent of children underweight | Number of countries |
|---|---|
| 16–21.45 | 23 |
| 21.45–26.9 | 4 |
| 26.9–32.35 | 9 |
| 32.35–37.8 | 7 |
| 37.8–43.25 | 6 |
| 43.25–48.7 | 1 |
Figure 2.124
What is the best estimate for the mean percentage of underweight children? What is the standard deviation? Which interval(s) could be considered unusual? Explain.
12. Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are shown in figure 2.125.
| Number of movies | Frequency |
|---|---|
| 0 | 5 |
| 1 | 9 |
| 2 | 6 |
| 3 | 4 |
| 4 | 1 |
Figure 2.125
- Find the sample mean,
 .
. - Find the approximate sample standard deviation, s.
13. Forty randomly selected students were asked the number of pairs of sneakers they owned. Let X represent the number of pairs of sneakers owned. The results are as follows:
| X | Frequency |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 8 |
| 4 | 12 |
| 5 | 12 |
| 6 | 0 |
| 7 | 1 |
Figure 2.126
- Find the sample mean,
 .
. - Find the sample standard deviation, s.
- Construct a histogram of the data.
- Complete the columns of the chart.
- Find the first quartile.
- Find the median.
- Find the third quartile.
- Construct a box plot of the data.
- What percent of the students owned at least five pairs?
- Find the 40th percentile.
- Find the 90th percentile.
- Construct a line graph of the data.
- Construct a stemplot of the data.
14. Following are the published weights (in pounds) of all of the team members of the San Francisco 49ers from a previous year:
177, 205, 210, 210, 232, 205, 185, 185, 178, 210, 206, 212, 184, 174, 185, 242, 188, 212, 215, 247, 241, 223, 220, 260, 245, 259, 278, 270, 280, 295, 275, 285, 290, 272, 273, 280, 285, 286, 200, 215, 185, 230, 250, 241, 190, 260, 250, 302, 265, 290, 276, 228, 265
- Organize the data from smallest to largest value.
- Find the median.
- Find the first quartile.
- Find the third quartile.
- Construct a box plot of the data.
- The middle 50% of the weights are from to .
- If our population were all professional football players, would the above data be a sample of weights or the population of weights? Why?
- If our population included every team member who ever played for the San Francisco 49ers, would the above data be a sample of weights or the population of weights? Why?
- Assume the population was the San Francisco 49ers. Find:
- the population mean, μ.
- the population standard deviation, σ.
- the weight that is two standard deviations below the mean.
- When Steve Young, quarterback, played football, he weighed 205 pounds. How many standard deviations above or below the mean was he?
- That same year, the mean weight for the Dallas Cowboys was 240.08 pounds with a standard deviation of 44.38 pounds. Emmit Smith weighed in at 209 pounds. With respect to his team, who was lighter, Smith or Young? How did you determine your answer?
15. One hundred teachers attended a seminar on mathematical problem solving. The attitudes of a representative sample of 12 of the teachers were measured before and after the seminar. A positive number for change in attitude indicates that a teacher’s attitude toward math became more positive. The 12 change scores are as follows:
3, 8, –1, 2, 0, 5, –3, 1, –1, 6, 5, –2
- What is the mean change score?
- What is the standard deviation for this population?
- What is the median change score?
- Find the change score that is 2.2 standard deviations below the mean.
16. Refer to the figures below and determine which of the following (a.-d.) are true and which are false. Explain your solution to each part in complete sentences.
- The medians for all three graphs are the same.
- We cannot determine if any of the means for the three graphs is different.
- The standard deviation for Graph (b) is larger than the standard deviation for Graph (a).
- We cannot determine if any of the third quartiles for the three graphs is different.
17. In a recent issue of the IEEE Spectrum, 84 engineering conferences were announced. Four conferences lasted two days. Thirty-six lasted three days. Eighteen lasted four days. Nineteen lasted five days. Four lasted six days. One lasted seven days. One lasted eight days. One lasted nine days. Let X represent the length (in days) of an engineering conference.
- Organize the data in a chart.
- Find the median, the first quartile, and the third quartile.
- Find the 65th percentile.
- Find the 10th percentile.
- Construct a box plot of the data.
- The middle 50% of the conferences last from days to days.
- Calculate the sample mean of days of engineering conferences.
- Calculate the sample standard deviation of days of engineering conferences.
- Find the mode.
- If you were planning an engineering conference, which would you choose as the length of the conference, mean, median, or mode? Explain.
- Give two reasons why you think that three-to-five days seem to be popular lengths for engineering conferences.
18. A survey of enrollment at 35 community colleges across the United States yielded the following figures:
6,414, 1,550, 2,109, 9,350, 21,828, 4,300, 5,944, 5,722, 2,825, 2,044, 5,481, 5,200, 5,853, 2,750, 10,012, 6,357, 27,000, 9,414, 7,681, 3,200, 17,500, 9,200, 7,380, 18,314, 6,557, 13,713, 17,768, 7,493, 2,771, 2,861, 1,263, 7,285, 28,165, 5,080, 11,622
- Organize the data into a chart with five intervals of equal width. Label the two columns “Enrollment” and “Frequency.”
- Construct a histogram of the data.
- If you were to build a new community college, which piece of information would be more valuable: the mode or the mean?
- Calculate the sample mean.
- Calculate the sample standard deviation.
- A school with an enrollment of 8,000 would be how many standard deviations away from the mean?
19. Let X represent the number of days per week that 100 clients use a particular exercise facility.
| x | Frequency |
|---|---|
| 0 | 3 |
| 1 | 12 |
| 2 | 33 |
| 3 | 28 |
| 4 | 11 |
| 5 | 9 |
| 6 | 4 |
Figure 2.128
a. What is the 80th percentile?
-
- 5
- 80
- 3
- 4
b. The number that is 1.5 standard deviations BELOW the mean is approximately .
-
- 0.7
- 4.8
- –2.8
- Cannot be determined
20. Suppose that a publisher conducted a survey asking adult consumers the number of fiction paperback books they had purchased in the previous month. The results are summarized in the figure below.
| Number of books | Frequency | Relative frequency |
|---|---|---|
| 0 | 18 | |
| 1 | 24 | |
| 2 | 24 | |
| 3 | 22 | |
| 4 | 15 | |
| 5 | 10 | |
| 7 | 5 | |
| 9 | 1 |
Figure 2.129
- Are there any outliers in the data? Use an appropriate numerical test involving the IQR to identify outliers, if any, and clearly state your conclusion.
- If a data value is identified as an outlier, what should be done about it?
- Are any data values further than two standard deviations away from the mean? In some situations, statisticians may use this criteria to identify data values that are unusual compared to the other data values. (Note that this criteria is most appropriate to use for data that is mound-shaped and symmetric, rather than for skewed data.)
- Do parts a. and c. of this problem give the same answer?
- Examine the shape of the data. Which part, a. or c., of this question gives a more appropriate result for this data?
- Based on the shape of the data which is the most appropriate measure of center for this data, mean, median or mode?
21. This figure contains the total number of deaths worldwide as a result of earthquakes for the period from 2000 to 2012.
| Year | Total number of deaths |
|---|---|
| 2000 | 231 |
| 2001 | 21,357 |
| 2002 | 11,685 |
| 2003 | 33,819 |
| 2004 | 228,802 |
| 2005 | 88,003 |
| 2006 | 6,605 |
| 2007 | 712 |
| 2008 | 88,011 |
| 2009 | 1,790 |
| 2010 | 320,120 |
| 2011 | 21,953 |
| 2012 | 768 |
| Total | 823,856 |
Figure 2.130
Answer each of the following questions and check your answers below.
- What is the frequency of deaths measured from 2006 through 2009?
- What percentage of deaths occurred after 2009?
- What is the relative frequency of deaths that occurred in 2003 or earlier?
- What is the percentage of deaths that occurred in 2004?
- What kind of data are the numbers of deaths?
- The Richter scale is used to quantify the energy produced by an earthquake. Examples of Richter scale numbers are 2.3, 4.0, 6.1, and 7.0. What kind of data are these numbers?
22. The following figure contains the total number of fatal motor vehicle traffic crashes in the United States for the period from 1994 to 2011.
| Year | Total number of crashes | Year | Total number of crashes |
|---|---|---|---|
| 1994 | 36,254 | 2004 | 38,444 |
| 1995 | 37,241 | 2005 | 39,252 |
| 1996 | 37,494 | 2006 | 38,648 |
| 1997 | 37,324 | 2007 | 37,435 |
| 1998 | 37,107 | 2008 | 34,172 |
| 1999 | 37,140 | 2009 | 30,862 |
| 2000 | 37,526 | 2010 | 30,296 |
| 2001 | 37,862 | 2011 | 29,757 |
| 2002 | 38,491 | Total | 653,782 |
| 2003 | 38,477 |
Figure 2.131
Answer the following questions.
- What is the frequency of deaths measured from 2000 through 2004?
- What percentage of deaths occurred after 2006?
- What is the relative frequency of deaths that occurred in 2000 or before?
- What is the percentage of deaths that occurred in 2011?
- What is the cumulative relative frequency for 2006? Explain what this number tells you about the data.
23. Fifty part-time students were asked how many courses they were taking this term. The (incomplete) results are shown below:
| Number of courses | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 1 | 30 | 0.6 | |
| 2 | 15 | ||
| 3 |
Figure 2.132
Fill in the blanks in the figure above.
- What percent of students take exactly two courses?
- What percent of students take one or two courses?
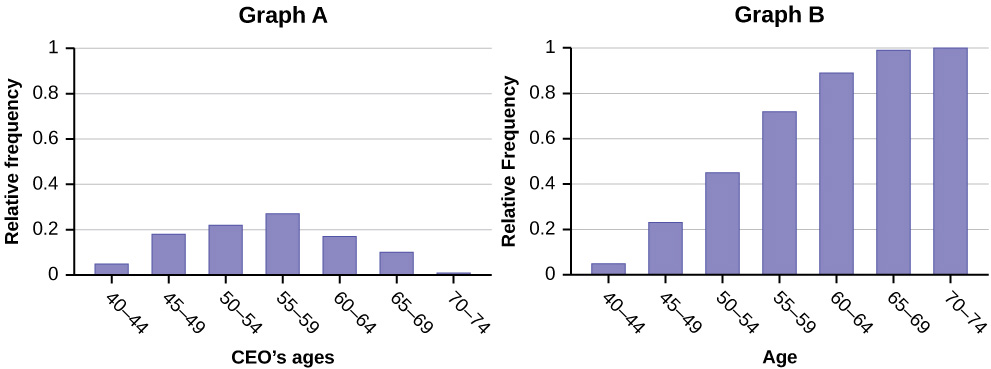
24. Forbes magazine published data on the best small firms in 2012. These were firms which had been publicly traded for at least a year, had a stock price of at least $5 per share, and had reported annual revenue between $5 million and $1 billion. The figure below shows the ages of the chief executive officers for the top 60 ranked firms.
| Age | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 40–44 | 3 | ||
| 45–49 | 11 | ||
| 50–54 | 13 | ||
| 55–59 | 16 | ||
| 60–64 | 10 | ||
| 65–69 | 6 | ||
| 70–74 | 1 |
Figure 2.133
- What is the frequency for CEO ages between 54 and 65?
- What percentage of CEOs are 65 years or older?
- What is the relative frequency of ages under 50?
- What is the cumulative relative frequency for CEOs younger than 55?
- Which graph shows the relative frequency, and which shows the cumulative relative frequency?
25. The figure below contains data on hurricanes that have made direct hits on the US between 1851 and 2004. A hurricane is given a strength category rating based on the minimum wind speed generated by the storm.
| Category | Number of direct hits | Relative frequency | Cumulative frequency |
|---|---|---|---|
| 1 | 109 | 0.3993 | 0.3993 |
| 2 | 72 | 0.2637 | 0.6630 |
| 3 | 71 | 0.2601 | |
| 4 | 18 | 0.9890 | |
| 5 | 3 | 0.0110 | 1.0000 |
| Total = 273 |
Figure 2.135
a. What is the relative frequency of direct hits that were Category 4 hurricanes?
-
- 0.0768
- 0.0659
- 0.2601
- Not enough information to calculate
b. What is the relative frequency of direct hits that were AT MOST a Category 3 storm?
-
- 0.3480
- 0.9231
- 0.2601
- 0.3370
26. The following data are the shoe sizes of 50 male students. The sizes are discrete data since shoe size is measured in whole and half units only. Construct a histogram, and calculate the width of each bar or class interval, supposing you choose six bars.
9, 9, 9.5, 9.5, 10, 10, 10, 10, 10, 10, 10.5, 10.5, 10.5, 10.5, 10.5, 10.5, 10.5, 10.5
11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11.5, 11.5, 11.5, 11.5, 11.5, 11.5, 11.5
12, 12, 12, 12, 12, 12, 12, 12.5, 12.5, 12.5, 12.5, 14
27. The following data are the number of sports played by 50 student athletes. The number of sports is discrete data since sports are counted.
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2
3, 3, 3, 3, 3, 3, 3, 3
20 student athletes play one sport. 22 student athletes play two sports. 8 student athletes play three sports.
Fill in the blanks for the following sentence. Since the data consist of the numbers 1, 2, 3, and the starting point is 0.5, a width of one places the 1 in the middle of the interval 0.5 to , the 2 in the middle of the interval from to , and the 3 in the middle of the interval from to .
28. Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. 14 people answered that they generally sell three cars, 19 generally sell four cars, 12 generally sell five cars, 9 generally sell six cars, and 11 generally sell seven cars. Complete the table.
| Data value (number of cars) | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
Figure 2.136
- What does the frequency column sum to? Why?
- What does the relative frequency column sum to? Why?
- What is the difference between relative frequency and frequency for each data value?
- What is the difference between cumulative relative frequency and relative frequency for each data value?
- To construct the histogram for the data, determine appropriate minimum and maximum x and y values and the scaling. Sketch the histogram. Label the horizontal and vertical axes with words. Include numerical scaling.
29. Suppose that three book publishers were interested in the number of fiction paperbacks adult consumers purchase per month. Each publisher conducted a survey. In the survey, adult consumers were asked the number of fiction paperbacks they had purchased the previous month. The results are as follows:
| Number of books | Frequency | Relative frequency |
|---|---|---|
| 0 | 10 | |
| 1 | 12 | |
| 2 | 16 | |
| 3 | 12 | |
| 4 | 8 | |
| 5 | 6 | |
| 6 | 2 | |
| 8 | 2 |
Figure 2.137: Publisher A
| Number of books | Frequency | Relative frequency |
|---|---|---|
| 0 | 18 | |
| 1 | 24 | |
| 2 | 24 | |
| 3 | 22 | |
| 4 | 15 | |
| 5 | 10 | |
| 7 | 5 | |
| 9 | 1 |
Figure 2.138: Publisher B
| Number of books | Frequency | Relative frequency |
|---|---|---|
| 0-1 | 20 | |
| 2-3 | 35 | |
| 4-5 | 12 | |
| 6-7 | 2 | |
| 8-9 | 1 |
Figure 2.139: Publisher C
- Find the relative frequencies for each survey. Write them in the charts.
- Using either a graphing calculator, computer, or by hand, use the frequency column to construct a histogram for each publisher’s survey. For Publishers A and B, make bar widths of one. For Publisher C, make bar widths of two.
- In complete sentences, give two reasons why the graphs for Publishers A and B are not identical.
- Would you have expected the graph for Publisher C to look like the other two graphs? Why or why not?
- Make new histograms for Publisher A and Publisher B. This time, make bar widths of two.
- Now compare the graph for Publisher C to the new graphs for Publishers A and B. Are the graphs more similar or more different? Explain your answer.
30. Often, cruise ships conduct all on-board transactions (with the exception of gambling) on a cashless basis. At the end of the cruise, guests pay one bill that covers all onboard transactions. Suppose that 60 single travelers and 70 couples were surveyed as to their on-board bills for a seven-day cruise from Los Angeles to the Mexican Riviera. The following table is a summary of the bills for each group.
| Amount ($) | Frequency | Relative frequency |
|---|---|---|
| 51–100 | 5 | |
| 101–150 | 10 | |
| 151–200 | 15 | |
| 201–250 | 15 | |
| 251–300 | 10 | |
| 301–350 | 5 |
Figure 2.140: Singles
| Amount ($) | Frequency | Relative frequency |
|---|---|---|
| 100–150 | 5 | |
| 201–250 | 5 | |
| 251–300 | 5 | |
| 301–350 | 5 | |
| 351–400 | 10 | |
| 401–450 | 10 | |
| 451–500 | 10 | |
| 501–550 | 10 | |
| 551–600 | 5 | |
| 601–650 | 5 |
Figure 2.141: Couples
- Fill in the relative frequency for each group.
- Construct a histogram for the singles group. Scale the x-axis by $50 widths. Use relative frequency on the y-axis.
- Construct a histogram for the couples group. Scale the x-axis by $50 widths. Use relative frequency on the y-axis.
- Compare the two graphs:
- List two similarities between the graphs.
- List two differences between the graphs.
- Overall, are the graphs more similar or different?
- Construct a new graph by hand for the couples. Since each couple is paying for two individuals, instead of scaling the x-axis by $50, scale it by $100. Use relative frequency on the y-axis.
- Compare the graph for the singles with the new graph for the couples:
- List two similarities between the graphs.
- Overall, are the graphs more similar or different?
- How did scaling the couples graph differently change the way you compared it to the singles graph?
- Based on the graphs, do you think that single individuals spend the same amount, more, or less than individuals who are part of a couple? Explain why in one or two complete sentences.
31. Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are shown in Figure 2.142.
| Number of movies | Frequency | Relative frequency | Cumulative relative frequency |
|---|---|---|---|
| 0 | 5 | ||
| 1 | 9 | ||
| 2 | 6 | ||
| 3 | 4 | ||
| 4 | 1 |
Figure 2.142
- Construct a histogram of the data.
- Complete the columns of the chart.
32. Use the data to construct a line graph.
- In a survey, 40 people were asked how many times they visited a store before making a major purchase. The results are shown below.
Number of times in store Frequency 1 4 2 10 3 16 4 6 5 4 Figure 2.143
- In a survey, several people were asked how many years it has been since they purchased a mattress. The results are shown below.
Years since last purchase Frequency 0 2 1 8 2 13 3 22 4 16 5 9 Figure 2.144
- Several children were asked how many TV shows they watch each day. The results of the survey are shown below.
Number of TV shows Frequency 0 12 1 18 2 36 3 7 4 2 Figure 2.145
Figure Descriptions
Figure 2.59: Histogram consists of six bars with the y-axis in increments of two from zero through 16 and the x-axis in intervals of one from 0.5-6.5. Bars taper off to the right.
Figure 2.62: This is an overlay frequency polygon that matches the supplied data. The x-axis shows the grades, and the y-axis shows the frequency. Both lines follow the same pattern, peaking around grade=84.5.
Figure 2.73: This shows three box plots graphed over a number line from zero to 11. The box plots match the supplied data, and compare the countries’ results. The China box plot has a single whisker from zero to five. The Germany box plot’s median is equal to the third quartile, so there is a dashed line at right edge of box. The America box plot does not have a left whisker.
Figure 2.74: This is a box plot graphed over a number line from zero to 150. There is no first, or left, whisker. The box starts at the first quartile, zero, and ends at the third quartile, 80. A vertical, dashed line marks the median, 20. The second whisker extends the third quartile to the largest value, 150.
Figure 2.75: This shows two box plots graphed over number lines from zero to seven. The first whisker in the data one box plot extends from zero to two. The box begins at the firs quartile, two, and ends at the third quartile, five. A vertical, dashed line marks the median at four. The second whisker extends from the third quartile to the largest value, seven. The first whisker in the data two box plot extends from zero to 1.3. The box begins at the first quartile, 1.3, and ends at the third quartile, 2.5. A vertical, dashed line marks the medial at two. The second whisker extends from the third quartile to the largest value, seven.
Figure 2.76: This shows three box plots graphed over a number line from 25 to 80. The first whisker on the BMW 3 plot extends from 25 to 30. The box begins at the firs quartile, 30 and ends at the third quartile, 41. A vertical, dashed line marks the median at 34. The second whisker extends from the third quartile to 66. The first whisker on the BMW 5 plot extends from 31 to 40. The box begins at the firs quartile, 40, and ends at the third quartile, 55. A vertical, dashed line marks the median at 41. The second whisker extends from 55 to 64. The first whisker on the BMW 7 plot extends from 35 to 41. The box begins at the first quartile, 41, and ends at the third quartile, 59. A vertical, dashed line marks the median at 46. The second whisker extends from 59 to 68.
Figure 2.79: Three box plots with values between 0 and 100. Plot one has Q1 at 24, M at 34, and Q3 at 53; Plot two has Q1 at 18, M at 34, and Q3 at 45; Plot three has Q1 at 24, M at 25, and Q3 at 54.
Figure 2.85: This is a horizontal box plot graphed over a number line from zero to 13. The first whisker extends from the smallest value, zero, to the first quartile, two. The box begins at the first quartile and extends to third quartile, 12. A vertical, dashed line is drawn at median, 10. The second whisker extends from the third quartile to largest value, 13.
Figure 2.86: A box plot with values from zero to 105, with Q1 at 17, M at 33, and Q3 at 50.
Figure 2.96: A histogram showing the results of a survey. Of 111 respondents, five own one t-shirt costing more than $19, 17 own two, 23 own three, 39 own four, 25 own five, two own six, and no respondents own seven.
Figure 2.101: This is a bar graph that matches the supplied data. The x-axis shows the county high schools, and the y-axis shows the proportion of county students. Alabaster: 9%, Concordia: 24%, Genoa: 15%, Mocksville: 15%, Tynneson: 10%, West End: 29%
Figure 2.107: This dot plot matches the supplied data. The plot uses a number line from zero to 14. It shows two x’s over zero, four x’s over one, three x’s over two, one x over three, two x’s over the numbers four, five, six, and nine, and one x each over 10 and 14. There are no x’s over the numbers seven, eight, 11, 12, and 13.
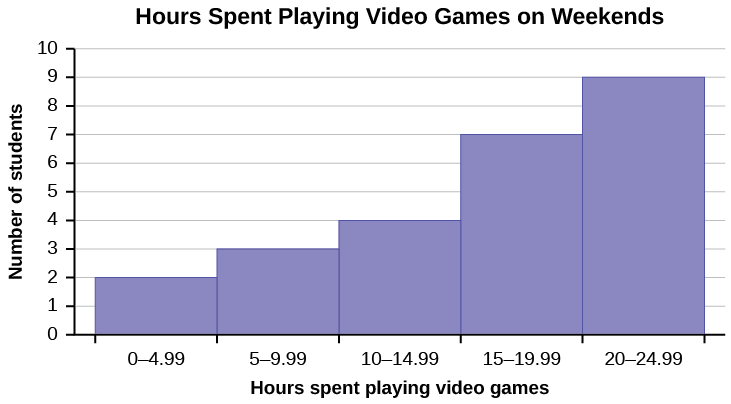
Figure 2.109: This is a histogram titled Hours Spent Playing Video Games on Weekends. The x-axis shows the number of hours spent playing video games with bars showing values at intervals of five. The y-axis shows the number of students. The first bar for 0 – 4.99 hours has a height of two. The second bar from 5 – 9.99 has a height of three. The third bar from 10 – 14.99 has a height of four. The fourth bar from 15 – 19.99 has a height of seven. The fifth bar from 20 – 24.99 has a height of nine.
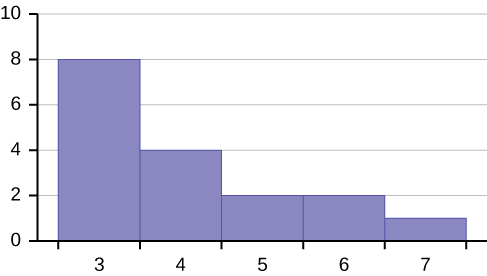
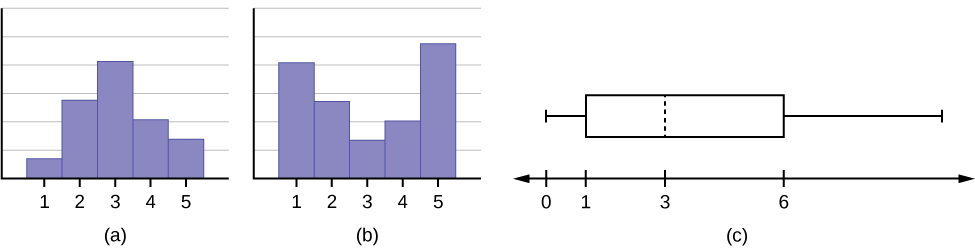
Figure 2.110: This is a histogram which consists of five adjacent bars with the x-axis split into intervals of one from three to seven. The bar heights peak at the first bar and taper lower to the right.
Figure 2.112: This shows two histograms. The first histogram shows a fairly symmetrical distribution with a mode of 6. The second histogram shows a uniform distribution.
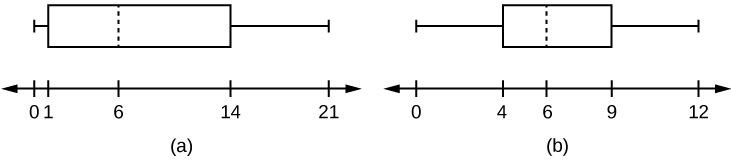
Figure 2.113: This shows two horizontal box plots. The first box plot is graphed over a number line from zero to 21. The first whisker extends from zero to one. The box begins at the first quartile, one, and ends at the third quartile, 14. A vertical, dashed line marks the median at six. The second whisker extends from the third quartile to the largest value, 21. The second box plot is graphed over a number line from zero to 12. The first whisker extends from zero to four. The box begins at the first quartile, four, and ends at the third quartile, nine. A vertical, dashed line marks the median at six. The second whisker extends from the third quartile to the largest value, 12.
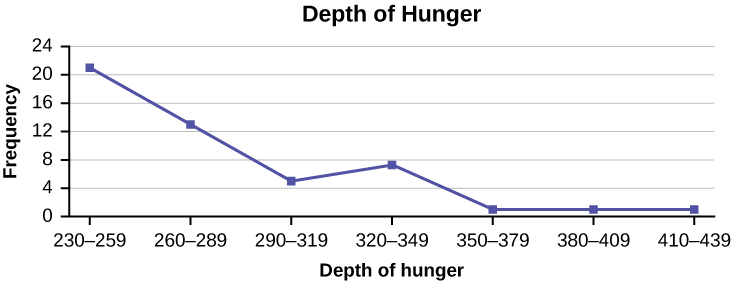
Figure 2.116: This is a frequency polygon that matches the supplied data. The x-axis shows the depth of hunger, and the y-axis shows the frequency. Values decrease, slightly increase, and then decrease and flatten out.
Figure 2.127: This shows three graphs. The first is a histogram with a mode of three and fairly symmetrical distribution between one (minimum value) and five (maximum value). The second graph is a histogram with peaks at one (minimum value) and five (maximum value) with three having the lowest frequency. The third graph is a box plot. The first whisker extends from zero to one. The box begins at the firs quartile, one, and ends at the third quartile, six. A vertical, dashed line marks the median at three. The second whisker extends from six on.
Figure 2.134: Graph A is a bar graph with seven bars. The x-axis shows CEO’s ages in intervals of five years starting with 40 – 44. The y-axis shows the relative frequency in intervals of 0.2 from zero to one. The highest relative frequency shown is 0.27. Graph B is a bar graph with seven bars. The x-axis shows CEO’s ages in intervals of five years starting with 40 – 44. The y-axis shows relative frequency in intervals of 0.2 from zero to one. The highest relative frequency shown is one.
References
Figures
Figure 2.59: Figure 2.6 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/2-2-histograms-frequency-polygons-and-time-series-graphs
Figure 2.62: Figure 2.9 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-2-histograms-frequency-polygons-and-time-series-graphs
Figure 2.73: Figure 2.45 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-homework
Figure 2.74: Figure 2.46 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-homework
Figure 2.75: Figure 2.47 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-homework
Figure 2.76: Figure 2.46 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/2-homework
Figure 2.79: Figure 2.47 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/2-bringing-it-together-homework
Figure 2.85: Figure 2.43 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-homework
Figure 2.86: Figure 2.44 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-homework
Figure 2.96: Figure from OpenStax Introductory Business Statistics (2012) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-business-statistics/pages/2-homework
Figure 2.101: Figure 2.54 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/2-solutions
Figure 2.107: Figure 2.24 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-6-skewness-and-the-mean-median-and-mode
Figure 2.109: Figure 2.25 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-6-skewness-and-the-mean-median-and-mode
Figure 2.110: Figure 2.7.9 from LibreTexts Introductory Statistics (2020) (CC BY 4.0). Retrieved from https://stats.libretexts.org/Bookshelves/Introductory_Statistics/Book%3A_Introductory_Statistics_(OpenStax)/02%3A_Descriptive_Statistics/2.07%3A_Skewness_and_the_Mean_Median_and_Mode
Figure 2.112: Figure 2.9.1 from LibreTexts Introductory Business Statistics (2020) (CC BY 4.0). Retrieved from https://biz.libretexts.org/Courses/Gettysburg_College/MGT_235%3A_Introductory_Business_Statistics/02%3A_Descriptive_Statistics/2.09%3A_Homework
Figure 2.113: Figure 2.51 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-bringing-it-together-homework
Figure 2.116: Figure 2.58 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-solutions
Figure 2.127: Figure 2.52 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/statistics/pages/2-bringing-it-together-homework
Figure 2.134: Figure 1.11 from OpenStax Introductory Business Statistics (2012) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-business-statistics/pages/1-homework
Text
“State & County QuickFacts: Quick, easy access to facts about people, business, and geography,” U.S. Census Bureau. http://quickfacts.census.gov/qfd/index.html (accessed May 1, 2013).
“Table 5: Direct hits by mainland United States Hurricanes (1851-2004),” National Hurricane Center, http://www.nhc.noaa.gov/gifs/table5.gif (accessed May 1, 2013).
“Levels of Measurement,” http://infinity.cos.edu/faculty/woodbury/stats/tutorial/Data_Levels.htm (accessed May 1, 2013).
David Lane. “Levels of Measurement,” Connexions, http://cnx.org/content/m10809/latest (accessed May 1, 2013).
Dekker, Marcel. Data on annual homicides in Detroit, 1961–73 in Gunst & Mason, Regression Analysis and its Application.
“Timeline: Guide to the U.S. Presidents: Information on every president’s birthplace, political party, term of office, and more.” Scholastic, 2013. Available online at http://www.scholastic.com/teachers/article/timeline-guide-us-presidents (accessed April 3, 2013).
“Presidents.” Fact Monster. Pearson Education, 2007. Available online at http://www.factmonster.com/ipka/A0194030.html (accessed April 3, 2013).
“Food Security Statistics.” Food and Agriculture Organization of the United Nations. Available online at http://www.fao.org/economic/ess/ess-fs/en/ (accessed April 3, 2013).
“Consumer Price Index.” United States Department of Labor: Bureau of Labor Statistics. Available online at http://data.bls.gov/pdq/SurveyOutputServlet (accessed April 3, 2013).
“CO2 emissions (kt).” The World Bank, 2013. Available online at http://databank.worldbank.org/data/home.aspx (accessed April 3, 2013).
“Births Time Series Data.” General Register Office For Scotland, 2013. Available online at http://www.gro-scotland.gov.uk/statistics/theme/vital-events/births/time-series.html (accessed April 3, 2013).
“Demographics: Children under the age of 5 years underweight.” Indexmundi. Available online at http://www.indexmundi.com/g/r.aspx?t=50&v=2224&aml=en (accessed April 3, 2013).
Gunst, Richard, Robert Mason. Regression Analysis and Its Application: A Data-Oriented Approach. CRC Press: 1980.
“Overweight and Obesity: Adult Obesity Facts.” Centers for Disease Control and Prevention. Available online at https://web.archive.org/web/20130917120224/https://www.cdc.gov/obesity/data/adult.html (accessed September 13, 2013).
Burbary, Ken. Facebook Demographics Revisited – 2001 Statistics, 2011. Available online at http://www.kenburbary.com/2011/03/facebook-demographics-revisited-2011-statistics-2/ (accessed August 21, 2013).
“9th Annual AP Report to the Nation.” CollegeBoard, 2013. Available online at http://apreport.collegeboard.org/goals-and-findings/promoting-equity (accessed September 13, 2013).
Data from West Magazine.
Cauchon, Dennis, Paul Overberg. “Census data shows minorities now a majority of U.S. births.” USA Today, 2012. Available online at http://usatoday30.usatoday.com/news/nation/story/2012-05-17/minority-birthscensus/55029100/1 (accessed April 3, 2013).
Data from the United States Department of Commerce: United States Census Bureau. Available online at http://www.census.gov/ (accessed April 3, 2013).
“1990 Census.” United States Department of Commerce: United States Census Bureau. Available online at http://www.census.gov/main/www/cen1990.html (accessed April 3, 2013).
Data from San Jose Mercury News.
Data from Time Magazine; survey by Yankelovich Partners, Inc.
Data from The World Bank, available online at http://www.worldbank.org (accessed April 3, 2013).
“Demographics: Obesity – adult prevalence rate.” Indexmundi. Available online at http://www.indexmundi.com/g/r.aspx?t=50&v=2228&l=en (accessed April 3, 2013).
Data from Microsoft Bookshelf.
King, Bill.“Graphically Speaking.” Institutional Research, Lake Tahoe Community College. Available online at http://www.ltcc.edu/web/about/institutional-research (accessed April 3, 2013).
- “Presidents.” Fact Monster. Pearson Education, 2007. Available online at http://www.factmonster.com/ipka/A0194030.html (accessed April 3, 2013). ↵
- “Food Security Statistics.” Food and Agriculture Organization of the United Nations. Available online at http://www.fao.org/economic/ess/ess-fs/en/ (accessed April 3, 2013). ↵
- Data from West Magazine. ↵
- “CO2 emissions (kt).” The World Bank, 2013. Available online at http://databank.worldbank.org/data/home.aspx (accessed April 3, 2013). ↵
- “Births Time Series Data.” General Register Office For Scotland, 2013. Available online at http://www.gro-scotland.gov.uk/statistics/theme/vital-events/births/time-series.html (accessed April 3, 2013). ↵
- Data on annual homicides in Detroit, 1961–73, from Gunst & Mason’s book ‘Regression Analysis and its Application’, Marcel Dekker ↵
- Data from West Magazine ↵
- “Overweight and Obesity: Adult Obesity Facts.” Centers for Disease Control and Prevention. Available online at https://web.archive.org/web/20130917120224/https://www.cdc.gov/obesity/data/adult.html (accessed September 13, 2013). ↵
- “Overweight and Obesity: Adult Obesity Facts.” Centers for Disease Control and Prevention. Available online at https://web.archive.org/web/20130917120224/https://www.cdc.gov/obesity/data/adult.html (accessed September 13, 2013). ↵
- “Demographics: Obesity – adult prevalence rate.” Indexmundi. Available online at http://www.indexmundi.com/g/r.aspx?t=50&v=2228&l=en (accessed April 3, 2013). ↵
- “Demographics: Children under the age of 5 years underweight.” Indexmundi. Available online at http://www.indexmundi.com/g/r.aspx?t=50&v=2224&aml=en (accessed April 3, 2013). ↵
- “Demographics: Obesity – adult prevalence rate.” Indexmundi. Available online at http://www.indexmundi.com/g/r.aspx?t=50&v=2228&l=en (accessed April 3, 2013). ↵
- “Demographics: Children under the age of 5 years underweight.” Indexmundi. Available online at http://www.indexmundi.com/g/r.aspx?t=50&v=2224&aml=en (accessed April 3, 2013). ↵

