3.5 Cautions about Regression

Adapted by John Morgan Russell; from Barbara Illowsky and Susan Dean, David Diez, Mine Cetinkaya-Rundel and Christopher D. Barr; Julie Vu and David Harrington

3.5 Cautions about Regression

While regression is a very useful and powerful tool, it is also commonly misused. The main things we need to keep in mind when interpreting our results are:

1. Linearity
2. Correlation (or association) does not imply causation
3. Extrapolation
4. Outliers and influential points

Linearity

Remember, it is always important to plot a scatter diagram first. If the scatter plot indicates that there is a linear relationship between the variables, then it is reasonable to use the methods we are discussing.

Correlation Does Not Imply Causation

Even when there is an apparent linear relationship and a reasonable value of r, there can always be confounding or lurking variables at work. Be wary of spurious correlations and make sure the connection you are making makes sense!

There are also often situations where it may not be clear which variables affect each other. Does lack of sleep lead to higher stress levels, or do high stress levels lead to lack of sleep? Which came first, the chicken or the egg? Sometimes these may not be answerable, but at least we are able to show an association there.

Extrapolation

Remember, it is always important to plot a scatter diagram first. If the plot suggests the variables have a linear relationship, then it is reasonable to use a best-fit line to make predictions for y given x within the domain of x values in the sample data, though not necessarily for x values outside that domain. The process of predicting inside of the observed x values observed in the data is called interpolation. The process of predicting outside of the observed x values observed in the data is called extrapolation.

Recall our example from the previous section. You could use the line to predict the final exam score for a student who earned a grade of 73 on the third exam. You should NOT use the line to predict the final exam score for a student who earned a grade of 50 on the third exam, because 50 is not within the domain of the x values in the sample data, which are between 65 and 75.

To understand just how unreliable the prediction can be outside of the observed x values observed in the data, make the substitution x = 90 in the equation:

$\stackrel{^}{y}=-173.51+4.83\left(90\right)=261.19$

The final exam score is predicted to be 261.19. The largest a final exam score could be is 100.

Outliers and Influential Points

In some scatter plots, there may be points that stick out. How they stick out is important in the bivariate case. Outliers are points that stick out from the rest of the group in a single variable. We can identify outliers in univariate data using the fence rules.

In addition to outliers, a sample may contain one or more points that are called influential points. Influential points are observed data points that do not follow the trend of the rest of the data. These points could have a big effect on the slope of the regression line calculation. To begin to identify an influential point, you can remove it from the dataset and see if the slope of the regression line changes significantly.

If a point is an outlier, does that necessarily make it an influential point (or vice versa)? The left graph of Figure 3.19 shows two points that stick out. One point is likely an outlier in y, but it still fits the trend. Therefore, it is not an influential point. The second point is influential (does not fit the trend) but does not appear to be an outlier in x or y. The right graph of Figure 3.19 shows a point that is both and outlier and an influential point. In summary, outliers are a univariate idea, influential points are bivariate ideas, and one does not imply the other.

Figure 3.19: Outliers and influential points. Figure description available at the end of the section.

How do we handle these unusual points? Sometimes, they should not be included in the analysis of the data. It is possible that an outlier or influential point is a result of erroneous data. Other times, they may hold valuable information about the population under study and should remain included in the data—especially when an outlier that is not an influential point may help us to not have to extrapolate. The key is to examine carefully what causes a data point to be an outlier and/or influential point.

Identifying Outliers and/or Influential Points

Many computers and calculators can be used to identify outliers from the data. Computer output for regression analysis will often identify both outliers and influential points so that you can examine them.

We know how to find outliers in a single variable using fence rules and box plots. However, we would like some guidelines as to how far away a point needs to be in order to be considered an influential point. Outliers also have large “errors,” where the error, also known as the residual, is the vertical distance from the line to the point. As a rough rule of thumb, we can flag any point that is located further than two standard deviations above or below the best-fit line as an outlier. The standard deviation used is the regression standard error of the residuals or errors. Another method used can be to “standardize” (more on this in CH4) the residuals, essentially calculating a Z-score. We already know that Z-scores outside of ±2 are “unusual” and we can say the same about standardized residuals.

We can do this visually in the scatter plot by drawing an extra pair of lines that are two standard deviations above and below the best-fit line. Any data points that are outside this extra pair of lines are flagged as potential outliers. We can also do this numerically by calculating each residual and comparing it to twice the standard deviation. The graphical procedure is shown in the example below, followed by the numerical calculations in the next example. You would generally need to use only one of these methods.

Example

Continuing with the example from the previous section, you can determine whether there are outliers in the student exam scores If there is an outlier, as an exercise, delete it and fit the remaining data to a new line. For this example, the new line ought to fit the remaining data better. This means the SSE should be smaller and the correlation coefficient ought to be closer to 1 or –1.

Here it is easy to identify the outliers graphically and visually. If we were to measure the vertical distance from any data point to the corresponding point on the line of best fit and that distance were equal to two or more standard deviations (±2s), then we would consider the data point to be “too far” from the line of best fit. We need to find and graph the lines that are two standard deviations below and above the regression line. Any points that are outside these two lines are outliers. We will call these lines Y2 and Y3:

ŷ = –173.5 + 4.83x is the line of best fit.
Let Y2 = –173.5 + 4.83x –2(16.4)
Let Y3 = –173.5 + 4.83x + 2(16.4)

Notice Y2 and Y3 have the same slope as the line of best fit.

If we graph the scatter plot with the best-fit line in equation and two dotted lines (Y2 and Y3) representing ±2s from the line, you will find the point x = 65, y = 175, which is the only data point that is not between lines. The outlier is the student who had a grade of 65 on the third exam and 175 on the final exam; this point is further than two standard deviations away from the best-fit line.

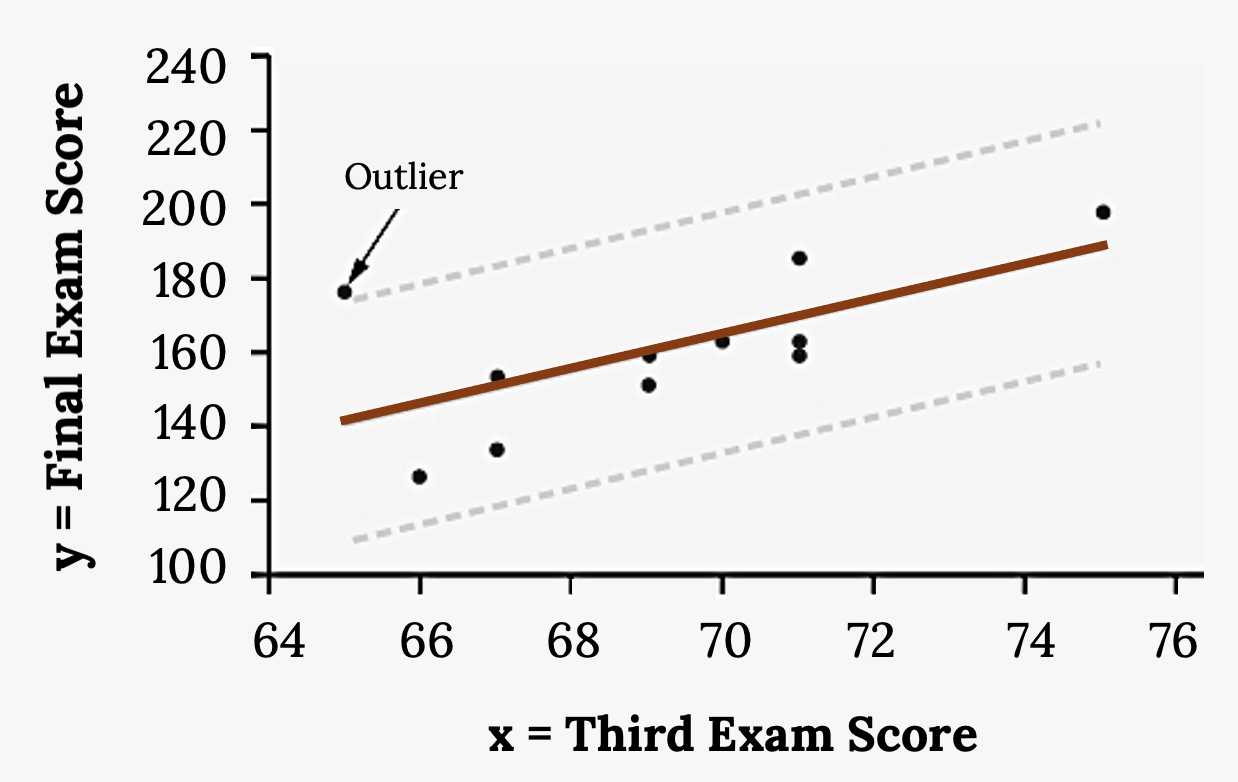
Your Turn!

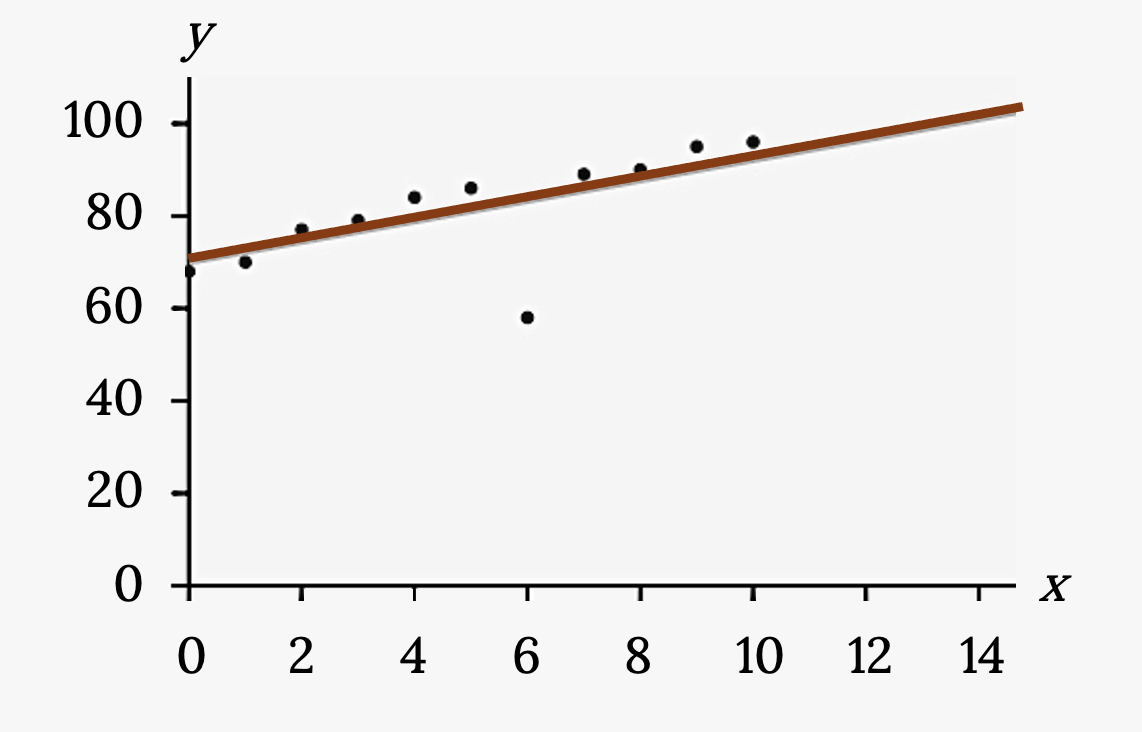
Identify the potential outlier in the scatter plot by drawing two separate lines. Suppose the standard deviation of the residuals or errors (s) is approximately s = 8.6.

Residuals

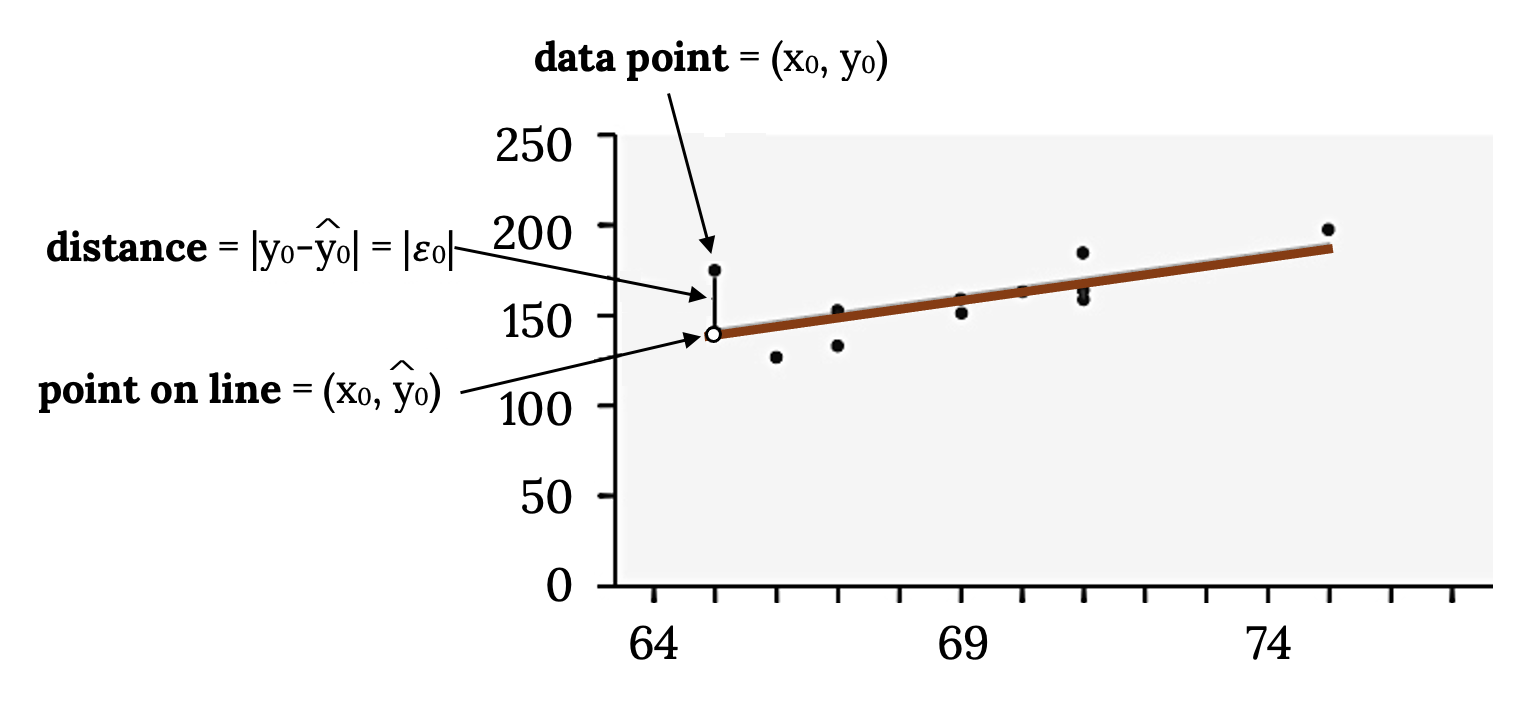
In the process of numerically identifying outliers and influential points, residuals are one of the most important tools and are found with the formula y₀ – ŷ₀ = ε₀ (ε = the Greek letter epsilon). Though the residual is often called the error, it is not an error in the sense of a mistake. The absolute value of a residual measures the vertical distance between the actual value of y and the estimated value of y. In other words, it measures the vertical distance between the actual data point and the predicted point on the line.

If the observed data point lies above the line, the residual is positive, and the line underestimates the actual data value for y. If the observed data point lies below the line, the residual is negative, and the line overestimates that actual data value for y.

In the diagram below, y0 – ŷ0 = ε0 is the residual for the point shown. Here the point lies above the line, and the residual is positive.

Points that fall far from the line are points of high leverage; these points can strongly influence the slope of the least-squares line. If one of these high leverage points does appear to actually invoke its influence on the slope of the line, then we consider it an influential point. Usually we can say a point is influential if, had we fitted the line without it, the influential point would have been unusually far from the least-squares line. Let’s see how to do this mathematically.

Example

For each data point, you can calculate the residuals or errors as y_i – ŷ_i = ε_i for i = 1, 2, 3, …, 11. Each |ε| is a vertical distance. In the following table, the first two columns are the third exam and final exam data. The third column shows the predicted ŷ values calculated from the line of best fit: ŷ = –173.5 + 4.83x. The residuals have been calculated in the fourth column of the table using this formula: observed y value − predicted y value = y − ŷ.

$x$	$y$	$\hat{y}$	$y - \hat{y}$
65	175	140	175 – 140 = 35
67	133	150	133 – 150= –17
71	185	169	185 – 169 = 16
71	163	169	163 – 169 = –6
66	126	145	126 – 145 = –19
75	198	189	198 – 189 = 9
67	153	150	153 – 150 = 3
70	163	164	163 – 164 = –1
71	159	169	159 – 169 = –10
69	151	160	151 – 160 = –9
69	159	160	159 – 160 = –1

Figure 3.23: Calculating residuals

For this example, there are 11 ε values. If you square each ε and add, you get:

${\left({\epsilon }_{1}\right)}^{2}+{\left({\epsilon }_{2}\right)}^{2}+...+{\left({\epsilon }_{11}\right)}^{2}=\stackrel{11}{\underset{i\text{ }=\text{ }1}{\Sigma }}{\epsilon }^{2}$

This is called the sum of squared errors (SSE).

For our example, the calculation is as follows:

1. First, square each |y – ŷ|.

The squares are 35², 17², 16², 6², 19², 9², 3², 1², 10², 9², and 1².

2. Then, add (sum) all the |y – ŷ| squared terms. Recall that y_i – ŷ_i = ε_i.

$\stackrel{11}{\underset{i = 1}{\Sigma }}{\left(|{y}_{i}-{\stackrel{^}{y}}_{i}|\right)}^{2}=\stackrel{11}{\underset{i = 1}{\Sigma }}{\epsilon }_{i}{}^{2}$

= 352 + 172 + 162 + 62 + 192 + 92 + 32 + 12 + 102 + 92 + 12

= 2440 = SSE

The result, SSE, is the sum of squared errors.

s is the standard deviation of all the y − ŷ = ε values where n = the total number of data points. If each residual is calculated and squared, and the results are added, we get the SSE. The standard deviation of the residuals is calculated from the SSE as:

$s=\sqrt{\frac{SSE}{n-2}}$

NOTE: We divide by (n – 2) as the degrees of freedom (df) because the regression model involves two estimates.

For our example:

$s=\sqrt{\frac{2440}{11-2}}=16.47$

NOTE: Rather than calculate these ourselves, we can find s using the computer or calculator.

More on Influential Points

If we were to measure the vertical distance from any data point to the corresponding point on the line of best fit and that distance is at least 2s, then we would consider the data point to be “too far” from the line of best fit. We call that point a potential influential point.

Back to our example, multiply s by two:

(2)(16.47) = 32.94

This reveals that 32.94 is two standard deviations away from the mean of the y – ŷ values.

So for this example, if any of the |y – ŷ| values are at least 32.94, the corresponding (x, y) data point is a potential outlier.

We are looking for all data points for which the residual is greater than 2s = 2(16.4) = 32.8 or less than –32.8. Compare these values to the residuals in column four of the table. It appears all the |y – ŷ|’s are less than 31.29 except for the first one which is 35.

The formula |y – ŷ| ≥ (2)(s) gives us 35 > 31.29.

The only such data point is the student who had a grade of 65 on the third exam and 175 on the final exam; the residual for this student is 35.

How does the outlier affect the best-fit line? Numerically and graphically, we have identified the point (65, 175) as an outlier. We should re-examine the data for this point to see if there are any problems with the data. If there is an error, we should fix the error if possible or delete the data. If the data is correct, we would leave it in the dataset. For this problem, we will suppose that we examined the data and found that this outlier data was an error. As a learning experience, we will continue on and delete the outlier so that we can explore how it affects the results.

The next step is to compute a new best-fit line using the ten remaining points. The new line of best fit is ŷ = –355.19 + 7.39x, and the correlation coefficient (r) is 0.9121.

The new line with r = 0.9121 is a stronger correlation than the original (r = 0.6631) because r = 0.9121 is closer to one. This means that the new line is a better fit to the ten remaining data values. The line can better predict the final exam score given the third exam score. The point we deleted appears to be an influential point

It is often tempting to remove outliers and influential points. Don’t do this without a very good reason. Models that ignore exceptional (and interesting) cases often perform poorly. For instance, if a financial firm ignored the largest market swings—the “outliers”—they would soon go bankrupt from poorly thought-out investments.

When outliers are deleted, the researcher should either record that data was deleted and why, or the researcher should provide results both with and without the deleted data. If data is erroneous and the correct values are known (e.g., student one actually scored a 70 instead of a 65), then this correction can be made to the data.

With this new line of best fit in mind, let’s revisit the remaining ten data points from the exam score example in previous sections. What would a student who receives a 73 on the third exam expect to receive on the final exam? Is this the same as the prediction made using the original line?

Using the new line of best fit, ŷ = –355.19 + 7.39(73) = 184.28, a student who scored 73 points on the third exam would expect to earn 184 points on the final exam.
The original line predicted ŷ = –173.51 + 4.83(73) = 179.08, so the prediction using the new line with the outlier eliminated differs from the original prediction.

Your Turn!

The Consumer Price Index (CPI) measures the average change over time in the prices paid by urban consumers for consumer goods and services. The CPI affects nearly all Americans because of the many ways it is used. One of its biggest uses is as a measure of inflation. By providing information about price changes in the nation’s economy to government, business, and labor, the CPI helps them to make economic decisions. The President, Congress, and the Federal Reserve Board use the CPI’s trends to formulate monetary and fiscal policies. In the following table, x is the year and y is the CPI.

$x$	$y$	$x$	$y$
1915	10.1	1969	36.7
1926	17.7	1975	49.3
1935	13.7	1979	72.6
1940	14.7	1980	82.4
1947	24.1	1986	109.6
1952	26.5	1991	130.7
1964	31.0	1999	166.6

Figure 3.24: CPI Values

Draw a scatter plot of the data.
Calculate the least-squares line. Write the equation in the form ŷ = a + bx.
Draw the line on the scatter plot.
Find the correlation coefficient.

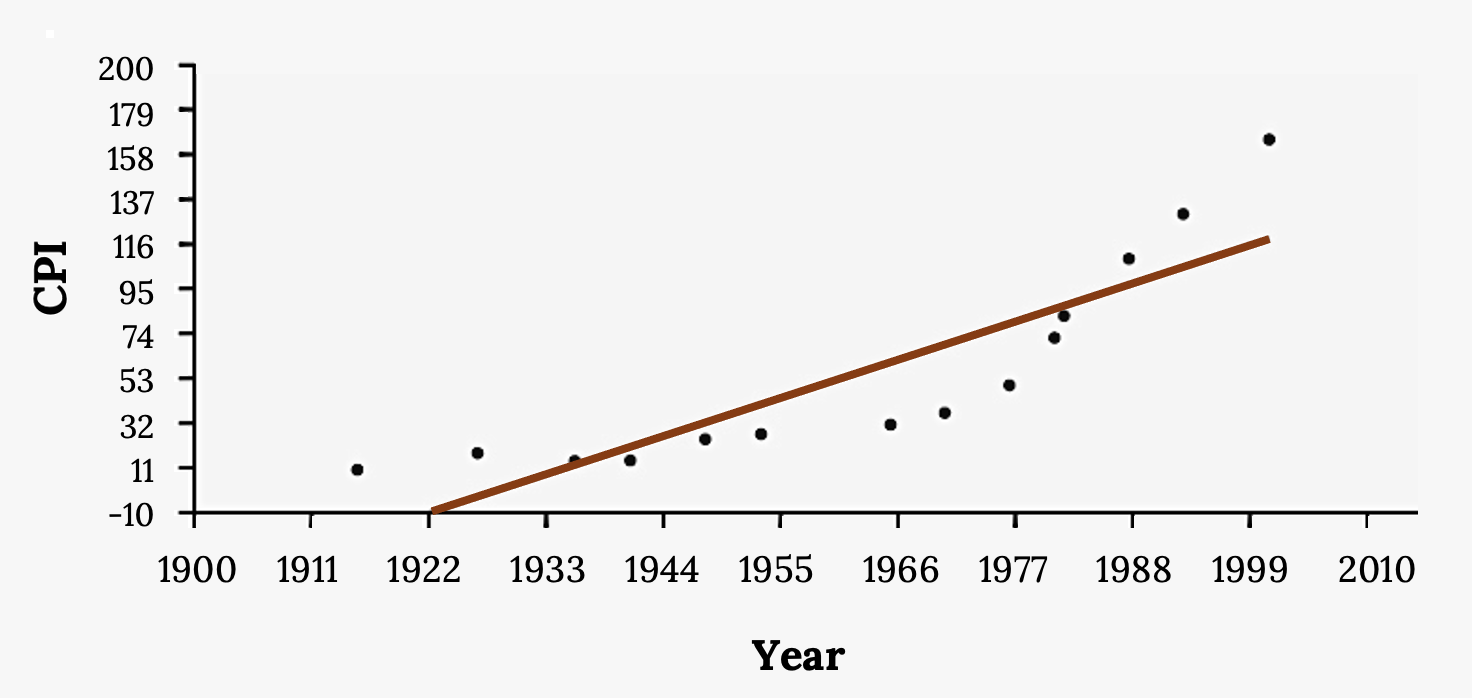
Figure 3.25: Scatter plot of CPI values. Figure description available at the end of the section.
What is the average CPI for the year 1990?
Comment on the appropriateness of this linear model. Do there appear to be any outliers or influential points?

Solution

a. The scatter plot should look similar to the one in (d).

b. ŷ = –3204 + 1.662x is the equation of the line of best fit.

c. [See image]

d. r = 0.8694

e. ŷ = –3204 + 1.662(1990) = 103.4 CPI

f. There are no outliers or influential points in the example. Notice the pattern of the points compared to the line. Although the correlation coefficient is significant, the pattern in the scatterplot indicates that a curve would be a more appropriate model to use than a line. In this example, a statistician should use other methods to fit a curve to this data, rather than model the data with a line. In addition to doing the calculations, it is always important to look at the scatterplot when deciding whether a linear model is appropriate.

Click here for more multimedia resources, including podcasts, videos, lecture notes, and worked examples.

Figure References

Figure 3.19: Kindred Grey (2024). Outliers and influential points. CC BY-SA 4.0.

Figure 3.20: Kindred Grey (2020). One method of identifying outliers in scatter plots. CC BY-SA 4.0. Adaptation of Figure 12.18 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/12-6-outliers

Figure 3.21: Kindred Grey (2020). Identify the outlier. CC BY-SA 4.0. Adaptation of Figure 12.19 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/12-6-outliers

Figure 3.22: Kindred Grey (2020). Residuals diagram. CC BY-SA 4.0. Adaptation of Figure 12.10 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/12-3-the-regression-equation

Figure 3.25: Kindred Grey (2020). Scatter plot of CPI values. CC BY-SA 4.0. Adaptation of Figure 12.20 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/12-6-outliers

Figure Descriptions

Figure 3.19: Left: scatterplot with an outlier in Y (there’s a point way high up above the rest) and an influential point (one that is not in line with the other points). Right: scatterplot where one point is both an outlier in x and an influential point

Figure 3.20: The same scatter plot of exam scores with a line of best fit. Two dashed lines run parallel to the line of best fit. The dashed lines run above and below the best fit line at equal distances. One data point falls outside the boundary created by the dashed lines—it is an outlier.

Figure 3.21: Scatterplot with dots in an almost perfect line from bottom left corner to top right corner of graph. There is one dot that does not follow this linear pattern.

Figure 3.22: The same scatter plot of exam scores with a line of best fit. One data point is highlighted along with the corresponding point on the line of best fit directly beneath it. Both points have the same x-coordinate. The distance between these two points illustrates how to compute the sum of squared errors.

Figure 3.25: Scatter plot and line of best fit of the consumer price index data, on the y-axis, and year data, on the x-axis. Moderately strong positive linear correlation.

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Significant Statistics: An Introduction to Statistics Copyright © 2024 by John Morgan Russell is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.