6.5 Behavior of Confidence Intervals for a Proportion

Confidence intervals (CI) for p behave similarly to intervals for μ, though there are a few subtle differences.

Calculating the Sample Size

If researchers desire a specific margin of error, then they can use the margin of error formula to calculate the required sample size, n.

Recall the margin of error for a population proportion is:

MoE = {z}_{\frac{\alpha }{2}} (\sqrt{\frac{\hat{p}\hat{q}}{n}})

Solving for n gives you an equation for the sample size:

n = (\frac{{z}_{\frac{\alpha }{2}}}{MoE})^{2} p(1 – p)

Recall the objective of a CI. If we are looking to estimate p, then we do not know what it is, even though it appears in this formula. So what do we plug in for p? We have a few options:

  • If you have prior information, such as a previous sample, and can calculate a point estimate 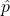\hat{p}, plug it in!
  • You can use your best guess at p.
  • You can use a “conservative” estimate of p, 0.5.

NOTE: Remember that \hat{q} = (1 – \hat{p}), though we do not know \hat{p} yet. Since we multiply \hat{p} and \hat{q} together, we make them both equal to 0.5. Why? Because \hat{p} \hat{q} = (0.5)(0.5) = 0.25 results in the largest possible product. (Try other products: (0.6)(0.4) = 0.24; (0.3)(0.7) = 0.21; (0.2)(0.8) = 0.16; and so on.) The largest possible product gives us the largest n. This gives us a large enough sample to be CL% confident that we are within three percentage points of the true population proportion.

 

 

Example

Suppose a mobile phone company wants to determine the current percentage of customers aged 50+ who use text messaging on their cell phones. How many customers aged 50+ should the company survey in order to be 90% confident that the estimated (sample) proportion is within three percentage points of the true population proportion of customers aged 50+ who use text messaging on their cell phones?

Solution

From the problem, we know that the margin of error is 0.03 (3% = 0.03) and zα/2 = z0.05 = 1.645 because the confidence level is 90%.

n = (\frac{z}{MoE})^{2} \hat{p} \hat{q} gives n = (\frac{1.645}{0.03})^{2} (0.5)(0.5)

Round the answer to the next higher value. The sample size should be 752 cell phone customers aged 50+ in order to be 90% confident that the estimated (sample) proportion is within three percentage points of the true population proportion of all customers aged 50+ who use text messaging on their cell phones.

Your Turn!

Suppose an internet marketing company wants to determine the current percentage of customers who click on ads on their smartphones. How many customers should the company survey in order to be 90% confident that the estimated proportion is within five percentage points of the true population proportion of customers who click on ads on their smartphones?

“Plus Four” Confidence Interval for p 

This is an alternative optional method for constructing a CI for p stemming from the continuity correction of the binomial approximation.

There is a certain amount of error introduced into the process of calculating a confidence interval for a proportion. Because we do not know the true proportion for the population, we are forced to use point estimates to calculate the appropriate standard deviation of the sampling distribution. Studies have shown that the resulting estimation of the standard deviation can be flawed.

 

Fortunately, there is a simple adjustment that allows us to produce more accurate confidence intervals. We simply pretend that we have four additional observations. Two of these observations are successes, and two are failures. The new sample size is then n + 4, and the new count of successes is x + 2.

Computer studies have demonstrated the effectiveness of this method. It should be used when the confidence level desired is at least 90% and the sample size is at least ten.

Example

A random sample of 25 statistics students was asked: “Have you smoked a cigarette in the past week?” Six students reported smoking within the past week. Use the “plus-four” method to find a 95% confidence interval for the true proportion of statistics students who smoke.

Solution

Six students out of 25 reported smoking within the past week, so x = 6 and n = 25. Because we are using the “plus-four” method, we will use x = 6 + 2 = 8 and n = 25 + 4 = 29.

\hat{p} = \frac{x}{n} = \frac{8}{29} ≈ 0.276

\hat{q} = 1 – \hat{p} = 1 – 0.276 = 0.724

Since CL = 0.95, we know α = 1 – 0.95 = 0.05 and α/2 = 0.025.

z0.025 = 1.96

Margin of error = ({z}_{\frac{\alpha }{2}}) (\sqrt{\frac{\hat{p}\hat{q}}{n}}) = (1.96)\sqrt{\frac{(0.276)(0.724)}{29}} ≈ 0.163.

\hat{p} – MoE = 0.276 – 0.163 = 0.113

\hat{p} + MoE = 0.276 + 0.163 = 0.439

We are 95% confident that the true proportion of all statistics students who smoke cigarettes is between 0.113 and 0.439.

Your Turn!

Out of a random sample of 65 freshmen at State University, 31 students have declared a major. Use the “plus-four” method to find a 96% confidence interval for the true proportion of freshmen at State University who have declared a major.

Additional Resources

QR code

Click here for additional multimedia resources, including podcasts, videos, lecture notes, and worked examples.

If you are using an offline version of this text, access the resources for this section via the QR code, or by visiting https://doi.org/10.7294/26207456.

definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Significant Statistics: An Introduction to Statistics Copyright © 2024 by John Morgan Russell is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book