7.2 Inference for Two Independent Sample Means
Suppose we have two independent samples of quantitative data. If there is no apparent relationship between the means, our parameter of interest is the difference in means, μ1-μ2, with a point estimate of ![]() –
– ![]() .
.
The comparison of two population means is very common. A difference between the two samples depends on both the means and their respective standard deviations. Very different means can occur by chance if there is great variation among the individual samples. In order to account for the variation, we take the difference of the sample means and divide by the standard error, standardizing the difference. We know that when conducting an inference for means, the sampling distribution we use (Z or t) depends on our knowledge of the population standard deviation.
Both Population Standard Deviations Known (Z)
Even though this situation is unlikely since population standard deviations are rarely known, we will begin demonstrating these ideas under the ideal circumstances. If we know both means’ sampling distributions are normal, the sampling distribution for the difference between the means is normal, and both populations must be normal. We can combine the standard errors of each sampling distribution to get a standard error of:
![]()
So the sampling distribution of ![]() –
– ![]() , assuming we know both standard deviations, is approximately:
, assuming we know both standard deviations, is approximately:
N ![]()
Therefore, the z-test statistic would be:
z = ![]()
Our confidence interval would be in the form (PE – MoE, PE + MoE), where our point estimate is ![]() –
– ![]() , and the margin of error is made up of:
, and the margin of error is made up of:
MoE = ![]()
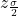 is the z critical value with area to the right equal to
is the z critical value with area to the right equal to 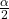
- SE is
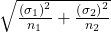
Since we rarely know one population’s standard deviation, much less two, the only situation where we might consider using this in practice is for two very large samples.
Both Population Standard Deviations Unknown (t)
Most likely, we will not know the population standard deviations, but we can estimate them using the two sample standard deviations from our independent samples. In this case, we will use a t sampling distribution with the following standard error:
![]()
Assumptions for the Difference in Two Independent Sample Means
Recall that we need to be able to assume an underlying normal distribution and no outliers or skewness in order to use the t-distribution. We can relax these assumptions as our sample sizes get bigger and can typically just use the Z distribution for very large sample sizes.
The remaining question concerns what we do for degrees of freedom when comparing two groups. One method requires a somewhat complicated calculation, but if you have access to a computer or calculator, this isn’t an issue. We can find a precise df for two independent samples as follows:
df = 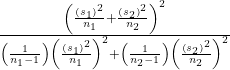
NOTE: The df are not always a whole number; you usually want to round down. It is not necessary to compute this by hand. Find a reliable technology to do this.
If you are working on your own without access to technology, the above formula could be daunting. Another method is to use a conservative estimate of the df: min(n1-1, n2-1).
Hypothesis Tests for the Difference in Two Independent Sample Means
Recall that the steps to a hypothesis test never change. When our parameter of interest is μ1-μ2, we are often interested in an effect between the two groups. In order to show an effect, we will have to first assume there is no difference by stating it in the null hypothesis as:
- Ho: μ1 – μ2 = 0 OR Ho: μ1 = μ2
- Ha: μ1 – μ2 (<, >, ≠) 0 OR Ha: μ1 (<, >, ≠) μ2
The t-test statistic is calculated as follows:
![]()
where:
- s1 and s2, the sample standard deviations, are estimates of σ1 and σ2, respectively.
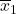 and
and 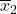 are the sample means. μ1 and μ2 are the population means. (NOTE: in the null, we are typically assuming μ1 – μ2 = 0.)
are the sample means. μ1 and μ2 are the population means. (NOTE: in the null, we are typically assuming μ1 – μ2 = 0.)
Confidence Intervals for the Difference in Two Independent Sample Means
Once we have identified a difference in a hypothesis test, we may want to estimate it. Our confidence interval would be of the form (PE – MoE, PE + MoE), where our point estimate is ![]() –
– ![]() , and the MoE is made up of:
, and the MoE is made up of:
MoE = ![]()
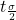 is the t critical value with area to the right equal to
is the t critical value with area to the right equal to 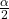
- SE is
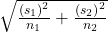
Additional Resources
The occurrence of one event has no effect on the probability of the occurrence of another event.
The standard deviation of a sampling distribution
The facet of statistics dealing with using a sample to generalize (or infer) about the population
The probability distribution of a statistic at a given sample size
The value that is calculated from a sample used to estimate an unknown population parameter
The number of objects in a sample that are free to vary
An interval built around a point estimate for an unknown population parameter

