Introduction
From the Author
There are numerous textbooks on aircraft aerodynamics and performance. Many of these do wonderful jobs of starting from the basics of physics and math and deriving all of the important fluid dynamic and flight dynamics equations that ultimately determine the way an airplane flies and behaves. These are, however, often written with so much mathematical and scientific rigor that students get lost in the math and fail to appreciate the physical importance of the assumptions made along the way and, therefore, don’t understand how to use the results. Other texts seek to simplify the rigor of the derivations and emphasize only the final equations, even to the point of inserting numerical values for many constants in the equations to such an extent that they only work when used with predetermined sets of assumptions and units. A common result is student misuse of the equations in situations where the assumptions are not valid or with inappropriate sets of units. In this book I will attempt a different approach, discussing the physics and mathematical bases while stressing the assumptions made in the development of the relationships that are presented, but I will do this without dwelling on all the little steps along the way. It will be assumed that the reader who wants more rigor in developing these relationships can go to the many other texts that do a very admirable job of presenting that level of detail.
The statement above does not mean I will avoid all derivations of equations but it does mean I will not go into a lot of detail, especially where derivations can get bogged down in mathematical detail that serves little purpose beyond appealing to math aficionados.
This book will seek to look into the basics of both airplane aerodynamics and aircraft performance. While we will occasionally look at other parts of the flight regime, the emphasis will be on subsonic flight and its associated incompressible flow. We will examine and emphasize the limitations of looking at flight in this manner and discuss a few of the consequences of venturing beyond these limits into the compressible flow regime, but we will not look in any detail into flight and performance at higher speeds. We will also keep our discussion of many important elements of aerodynamics at a very basic level, emphasizing general results more than detailed methods used to get those results. There are many fine textbooks in aerodynamics that are available to the reader who wishes to go beyond the level of this book and the student of aeronautical or aerospace engineering will undoubtedly use one or more of those texts in future courses.
The two primary areas of concern in this text are aerodynamics and performance. In general, aerodynamics involves studying the relationships of pressure and flow speed as air flows around a streamlined shape such as an airplane or a wing. If a flow over a wing gives a lower pressure on top of the wing than on the bottom, we have lift, and aerodynamics seeks to explain that phenomenon and examine how shaping the wing in both two and three dimensions can create more lift in a more efficient way. If the pressures on the front of the airplane or wing are greater than those at the back, we get drag, and the aerodynamicist wants to minimize this drag at the same time as the lift is maximized. It is also important to look at how those pressures are distributed over the wing because that distribution can influence the likelihood of the flow breaking away from the wing and causing higher drag or wing stall. The pressure distribution can also determine the nature of the flow over the wing or airplane right at the surface and this influences the kind of drag that results from the friction of the air moving over the surface. These forces (lift and drag) are the fundamental forces that will concern us when we look at airplane performance.
The pressure distributions over the wing and other parts of an airplane also determine the tendency of the plane to rotate around its center of gravity (center of mass) in ways that we refer to as pitch (nose up or down), roll (one wing up, the other down), or yaw (nose left or right). These types of motion are important to an entirely different subject, that of airplane dynamics, stability and control.
A third subject for later study that is strongly affected by these aerodynamic forces on the aircraft and its wing is structures. Obviously, the airplane must be designed to hold together under the stresses caused by these forces. The airplane structure must be as light as possible while giving the strength needed to resist damage under the worst of the aerodynamic loads for which the plane was designed. And we sometimes forget that the other primary role of the structure is to give the shape that is needed to produce the desired pressure and friction forces.
One thing we will attempt to do as we look at basic aerodynamics and performance is to make sure that we do not look at these topics in isolation, but consider their impact on aircraft dynamics and structural design. For example, we will find that a certain type of distribution of aerodynamic lift forces along the span of the wing from one tip to the other will produce an “ideal” or “minimum drag” loading. However, this ideal aerodynamic loading is not the ideal structural loading, and in the design of a real airplane, both needs must be considered. We will also find that a high “aspect ratio”, or a large ratio of wing span for a given wing area, will give both better aerodynamic performance and better airplane performance than a wing with a low “aspect ratio”. On the other hand, the wing that is best for lift and drag and overall airplane performance may not be very good for optimum aircraft dynamic performance in such things as roll maneuvers.
Two other very important things that will be emphasized in this text will be a rigorous attention to units and the need for continual reality checks to make sure we are getting results that are “in the ballpark”; i.e., that they make sense in the real world. Too often, it is inattention to these two subjects that cause students the most woe in getting the “right answers” on tests and in homework, and it was inattention to one of these subjects that resulted in a very expensive space mission to Mars missing the entire planet a couple of years ago.
Many engineering textbooks merely assume that all work will always be done in a particular unit system (usually SI) and that the equations developed include constants appropriate to the chosen system and no other. We will not do that. All equations in this text will be completely generic with respect to units, with no assumptions about the use of SI or English (American) or any other system of units. This is meant to force the student to carry appropriate units with every number and resolve those units as needed for the solution of the equation. This should, in fact, be helpful in assuring that the “answer” to the calculation is correct since, if the units come out wrong, it is a pretty good indication that the numbers are also wrong.
This approach will undoubtedly bother avid proponents of one unit system of another, those people who believe that only one unit system is “politically correct” and should always be used even if its users have absolutely no feel for the meaning or values of the units used. I believe that it is, nonetheless, important to have equations that force the user to take care to resolve both numbers and units for two reasons. First, resolving the units in the equations is, as mentioned above, a rather easy and important way to make sure that the “answer” is, indeed, correct. Second, regardless of how ideal our world would be if everyone used the same unit system for everything they do, that is not the case, and it is my experience after working with engineering faculty and students in Europe and Asia that few people really have a good physical feel for many of the basic SI units. I have been asked by French engineers what a Pascal is, and many fail to grasp that the Newton is a proper unit of weight because much of the world prefers to ignore the effects of gravity and work only with mass. Until I find a handful of people anywhere in the world who can tell me their weight in Newtons, without doing mental conversions from pounds (in the U. S.) or “stones” (in England) or converting from kilograms of mass, I will not be convinced that we can just assume that the use of SI units in textbooks eliminates unit problems.
This also relates to the important idea of gaining an appreciation for proper magnitudes of the properties that we will study in this text. I am always amazed when a student is perfectly happy turning in a paper in which she or he has calculated that a single engine, propeller driven airplane is cruising at Mach 2! It would seem apparent that the answer is very wrong. In reality, the student probably has done a calculation without paying attention to units and has come up with an answer of something like 2000 feet per second and hasn’t bothered to think that this is about twice the speed of sound. Perhaps if the answer had been calculated in miles per hour, the magnitude of the value would have made a bigger impression and set off a mental alarm. On the other hand, had the answer been found as 600 meters (metres?) per second, most American students would have no idea how fast this really is. Even in Britain, where highway speeds are still posted in miles per hour, students may not have immediately recognized that this answer violated an incompressible flow assumption. So, just as we would suspect that we had been cheated if we stepped on a coin operated scale and were told that we weighed 2500 pounds because we have a physical feel for the proper range of human weights, we need to develop a sense of “ballpark” answers for aerodynamic forces, speeds, aircraft ranges and endurance and similar parameters that we will encounter in this text.
The objective of this text is to provide a “stand alone” coverage of basic, subsonic, aircraft performance preceded by an introduction to the basics of aerodynamics that will provide a background sufficient to the understanding of the subjects to be studied in aircraft performance. Aircraft performance calculations are essentially the result of simply balancing the forces on an airplane, lift against weight and thrust against drag, and looking at how these balances work together and how they are affected by things like speed and altitude. To understand this balance we must know something about these aerodynamic forces that we call lift and drag and understand something about how they vary with speed and altitude. This will be our objective in the first three chapters, to learn about aerodynamics and to learn about how the properties of the atmosphere change with altitude. We will also try to gain some sense of how the pilot sees his or her operating environment using the instrumentation available in the cockpit and how that might relate to the performance and operation of the airplane.
Once we have looked at some aerodynamics we will begin to use our knowledge to explore the way an airplane performs. How fast or slow can it fly? How high can it climb and what is the rate of climb? How far can it glide? How far can it fly on a tank of fuel? All of these can be determined by just balancing forces. We will then look at a couple of cases where we must consider acceleration. These are takeoff/landing and turning.
Finally, we will take a look at how to try to balance all of the things we have learned about performance in order to design an airplane that will do everything we want; i.e., to takeoff and land in a desired distance and also climb at the desired rate, cruise at the target speed, etc.
Homework Problems
The homework problems at the end of each chapter build on the examples in the text to provide experience in working with the materials and theoretical methods presented in the text. Many of the problems ask for the plotting of graphs and graph paper is provided for that purpose. The first question many students will ask is: “Do I have to use the graph paper? Can’t I plot these using Excel or some other computer package?”
It is my feeling that there is value in learning to plot by hand and, in using these predimensioned plot axes, the student is shown some limit on the scope of the solution; i.e., if his or her graph won’t fit the provided scale, it is wrong! Plotting the data by hand offers the “opportunity” for the person doing the plotting to think a little about the points being plotted and to determine whether they make sense physically. Many aircraft performance calculations are related to flight “within the envelope” where the “envelope” is literally the area inside the curve on a plot and the visualization of such an envelope can help one understand what is happening. It is my experience that for some reason those who have their computer do the plot are much more likely to be perfectly happy with results that make no sense at all (that Mach 3 Cessna 152!) than are those who plot the results by hand, perhaps simply because hand plotting of results forces one to take the time to look at those results and not assume they are correct just because they were generated by a computer program.
In plotting data the actual data points which are calculated ( or obtained from experiment) should be shown with a small symbol such as a square or a circle or a triangle. The general curve should be faired through those points following a smooth curve or path and not as a game of connect the dots as computers are prone to do.
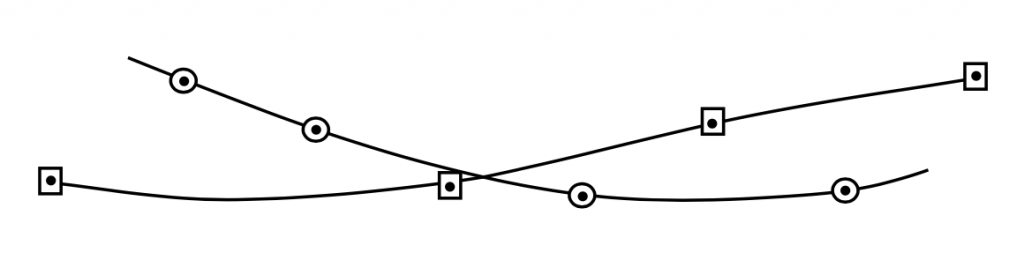
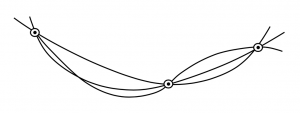
It should also be remembered that a minimum number of points are necessary to define a curve. Two data points tells nothing about the trends and three points are marginal. The student should remember that when plotting performance data he or she must plot enough points to get a good definition of the curve in the region where information is sought. For example, there is no way to tell from the three data points below where the minimum might lie.
References
Figure P1: Kindred Grey (2021). “Example Data Sets and Plotting Styles.” CC BY 4.0. Adapted from James F. Marchman (2004). CC BY 4.0. Available from https://archive.org/details/intro-hw-1
Figure P2: Kindred Grey (2021). “Curvature Uncertainty Due to Insufficient Data Points.” CC BY 4.0. Adapted from James F. Marchman (2004). CC BY 4.0. Available from https://archive.org/details/intro-hw-2

