5 The Wrecking Ball: Bias, Confounding, Interaction and Effect Modification
5.1 Sources of Study Errors
Studies will never be perfect. We start all of our work knowing this, but we should also control everything we can to make it the best it can be. We want a study with the best validity and reliability available. There are three things that can completely destroy or derail a study:
- Bias: A systematic error in how a study is designed.
- Confounding: A third related factor that distorts the relationship between exposure and outcome for all participants.
- Interaction and effect modification: Another third factor that distorts the relationship of exposure and outcome but does it differently for different participants.
Each of these concepts is better defined and explained on the following pages. Figure 5.1 shows us what could explain any association (e.g., a relative risk of 4.1 in a study) between a risk factor for disease and getting the disease. In statistics as in life, things can vary randomly. We might also see true causal associations. This is most often what we really want to see. For example, in the famous 1950 British Medical Journal paper “Smoking and Carcinoma of the Lung,” Drs. Doll and Hill specifically showed a causal and temporal relationship between smoking and lung cancer.[1] This was one of the first times this was proven and has served as the basis for tobacco policy around the world. However, even in their article, Drs. Doll and Hill had to consider whether bias or confounding skewed their study results. They concluded that was not the case.
| What can explain an association? | How can we look for or take care of it? |
|---|---|
| Random variability | Statistical precision estimates: p-value, confidence interval |
| Causal relationship | Bradford Hill criteria, randomization, regression, path analysis, rule out other possible explanations |
| Bias | Standardize questions, clear definitions, use objective data sources instead of or to supplement subjective data sources, plan ahead for attrition of participants, use validated measures |
| Confounding | Adjustment, restriction of study population, randomization, matching, regression |
| Interaction or effect modification | Present group specific results, restriction of study population |
Figure 5.1: Possible explanations for an association between a risk factor and a disease.
You recall validity from chapter 4. When we are talking about designing and carrying out different studies, strong study validity comes down to how you planned each study.
- If you design it right and follow the right steps, your study is valid and will have unbiased results. On average, the results will be correct.
- If you do not design it right and/or do not follow the right steps, it will be invalid and have biased results. On average, the results will be incorrect.
5.1.1 Bias
Bias is a systematic error in how a study is designed. Bias results from a design error, including the method of choosing participants or gathering information to define whether a participant has the exposure or disease. Bias is one thing that can alter the measure you created and make you think the answer to it is A when it is really B. This is also known as a false difference in a relationship between factors. As we can only do our own study, it is hard to determine whether our result is accurate. To determine if bias is confirmed to be present or how it may have influenced the answer we see would require infinite studies to see the truth. Instead we prevent bias best by:
- Using the appropriate study design
- Establishing valid and reliable methods of data collection
- Using appropriate analytic procedures
Most types of bias are either selection or information (figure 5.2):
- Selection: Error in how we picked participants
- Information: Error in how we obtain information (data) from participants
Types of bias can overlap, and rarely are we concerned with just one type of bias during a study. More specifically, selection bias is when individuals have different probabilities of being selected in the study sample according to their exposure and outcome. Selection bias means that the study does not have external validity (i.e., the results cannot be applied to any other population) and that the results will inaccurately represent the actual relationship being studied (i.e., compromised internal validity).
Information bias is when people systematically get placed in the wrong classification group for exposure and/or outcome (misclassification). When we make this mistake with everyone in the study, no matter their disease or exposure group, we consider it to be non-differential. Non-differential misclassification is when the misclassification of the exposure category is unrelated to the disease status and/or the misclassification of the disease category is unrelated to the exposure status.[2] When it makes a difference which group a subject is in (e.g., we only collect information incorrectly for controls), the bias is differential. Differential misclassification is when the misclassification of the exposure category is related to the disease status of the participant and/or if the misclassification of the disease status is related to the exposure category.[3] Information bias can also be failure to appropriately interpret the results or relationships seen in the data. Some people consider confounding to be a type of bias, so we have included it in figure 5.2. Misclassification can happen often in case-control and cohort studies. This concept is related to our prior discussion of sensitivity, specificity, validity, and reliability. If misclassification is present, we will not correctly calculate sensitivity or specificity. We also will have a false idea of the true validity or reliability of the answer from the study. Knowing how the misclassification or confounding occurs helps us decide what to do next analytically but certainly should involve a consultation with an epidemiologist or biostatistician to make sure the analysis is appropriate.
| Type | Definition | Example |
|---|---|---|
| Selection Bias | ||
| Selection bias | A bias that results in a sample population that is not representative of the population of interest and affects the internal validity of the study | Failure to confirm the age of participants prior to enrollment in the study results in needing to exclude 40 percent of the surveys captured |
| Volunteer bias / Self-selection bias | Those who volunteer for a study are clinically different than those who do not volunteer for the study. | People with a family history of cancer are more likely to volunteer for a study on breast cancer prevention. |
| Sampling bias | A bias that results in certain people having a greater chance of being selected than others and affects the external validity of the study | Choosing participants for a study of medical students by conveniently picking your friends to participate due to your relationship |
| Survivorship bias | A bias that results in only those who survived a disease being selected for a study | Patients who have few complications to COVID-19 may survive longer than patients who were hospitalized and so a study ten years later would capture people who had had milder disease. |
| Attrition bias | Participants who leave the study are different than the participants who stay. | Participants with comorbid conditions may leave the study early due to complications from those comorbidities, leaving the researcher with participants who have fewer comorbidities |
| Non-Response bias | Participants who do not respond to participate are different than the participants who choose to respond. | Participants who are older and less computer savvy are less likely to respond to requests by email to participate in a study. |
| Recall bias | Participants have difficulty remembering information or events from the past. | Patients may not recall whether they have ever had an exposure that is required to participate in the study. |
| Information Bias | ||
| Performing study | ||
| Recall bias | Participants have difficulty remembering information or events from the past. | Participants may not recall their blood type when asked and randomly select one that is incorrect. |
| Measurement bias | Data about the outcome, exposure, or other study factors are not accurately measured or categorized. | Study interviewers know a participant is an athlete and select “yes, concussion” no matter what the participant says. |
| Procedure bias | The administration of the study puts undue pressure on the participants, such as not enough time to complete a survey or too long a distance to complete a needed task. This could also mean that researchers or participants self-assign or nonrandomly assign people to study groups. | Participants at a factory are asked to fill out a survey about their supervisor in front of their supervisor at the beginning of a shift. |
| Observer-expectancy bias | Researchers influence respondents to answer a particular way to questions. | The researcher knows the patient is a case and asks the question in a way that suggests the correct answer is that there was an exposure. |
| Response bias | Participants are worried about social acceptability of their answer and may respond differently than is true. | Patients say that they eat 6–11 servings of fruits and vegetables daily when they actually eat fewer. |
| Interpreting results | ||
| Confounding bias | A factor that makes you misinterpret the relationship between the exposure and the outcome | The association between teenage smoking and packaging/store placement is not independent of the influence of growing up seeing their parents smoke. |
| Lead-time bias | Disease is diagnosed earlier but the true course of disease is the same length as those who did not have early diagnosis. | Minoritized patients have breast cancer detected later than nonminoritized patients and appear to have a shorter life expectancy than those who have their cancer detected earlier. |
| Length-time bias | Disease that develops slowly is more likely to be detected early and have a better prognosis. | Slow-growing fibroids are able to be detected earlier at annual visits and monitored or removed compared to fast-growing fibroids. |
| Reading about the study | ||
| Publication bias | When negative study results or very novel ideas are not published in favor of positive study results and “more interesting” topics | A manuscript is rejected by multiple journals for publication because none of the hypotheses was found to be true. |
Figure 5.2: Bias.
In a textbook from the International Agency for Research on Cancer and the World Health Organization, dos Santos Silva provided a series of questions (figure 5.3) that researchers should ask themselves to determine whether selection or information bias exists in their study.[4] These questions should optimally be asked prior to study execution and regularly during the course of study implementation, analysis, and reporting. Chapter 13 of the Cancer Epidemiology text by dos Santos Silva[5] provides more detail on the importance of these questions and other factors to consider to minimize bias. Note that many questions about selection relate to making sure that the same procedures are used for enrolling participants in a study, the process does not differ based on who is doing the recruitment or the disease or exposure status of the participant, and that the inclusion and exclusion criteria are very clear. Both are necessary to best define who should be in the study population and who you actually want to exclude.
Inclusion criteria is a definitive list of characteristics of participants that you want to enroll in the study and can be very minimal or very detailed. For example:
- Children who go to Alpha Elementary School
- Children between the ages of five and seven who go to Alpha Elementary School, are in kindergarten or first grade, have lived in town Alpha since birth, and who bring their own lunch to school
Exclusion criteria is a list of characteristics that participants should not have. These can also be minimal or very detailed. For example:
- Children in town Alpha who attend any school other than Alpha Elementary School at the present time
- Children younger than five or older than seven years, children who were not born in town Alpha or have not lived in town Alpha their entire lives, and children who eat prepared school meals or do not eat meals
| Selection bias | • Was the study population clearly defined? • What were the inclusion and exclusion criteria? • Were refusals, losses to follow-up, etc., kept to a minimum? • In cohort and intervention studies: Were the groups similar except for the exposure/intervention status? Was the follow-up adequate? Was it similar for all groups? • In case-control studies: Did the controls represent the population from which the cases arose? Was the identification and selection of cases and controls influenced by their exposure status? |
| Measurement bias | • Were the measurements as objective as possible? • Were the measurements as objective as possible? • Were the subjects and observers blind? • Were the observers and interviewers rigorously trained? • Were clearly written protocols used to standardize procedures in data collection? • Were the study subjects randomized to observers or interviewers? • Was information provided by the patient validated against any existing records? • Were the methods used for measuring the exposure(s) and outcome(s) of interest (e.g., questionnaire, laboratory assays) validated? |
| Were strategies built into the study design to allow assessment of the likely direction and magnitude of the bias? | |
Figure 5.3: How to check for bias in epidemiological studies.
One way to minimize selection bias is called case-based control selection. People who participate in health screenings such as mammograms are generally different from people who do not participate in these health screenings. They are more likely to have characteristics that are different (e.g., family history of disease or age), so comparing them to other people is akin to comparing apples and oranges. If we select our controls from the same pool of people that cases come from (i.e., case-based controls), the two groups will be more similar (e.g., Granny Smith apples compared to Gala apples). Our next example shows how we might avoid selection and information bias using case-based control selection.
Example: Selection bias and information bias avoidance
We want to do a study about long-term effects of ankle injuries from sport. As we work to define our specific study population, we think we want to select participants from emergency (ER) records. If we are not more specific about our study, we will have bias in our participant selection because our study answer will not apply to all people with ankle injuries from sport, just those who are seen in the ER. From what we know about SRI, people who go to the ER are more likely to have more severe injuries than those who do not go to the ER. They are also much more likely to have health insurance than those who do not go to the ER.
If the severity of the ankle injury is the same in the population that seeks treatment at the ER as in the population that did not seek treatment at the ER, there is limited selection bias due to where our cases come from. Severity is not the deciding factor in where to seek treatment.
However, because people are likely to select where and how they get treatment due to the severity of the injury, there is going to be selection bias in our study. To reduce the problem, we should reframe our research question to be the long-term effects of ankle injuries from sport that seek treatment in the ER. We selected a specific population. We might still end up with bias in our study, but the effect of it is lessened. This is also known as compensating bias, or the attempt to equalize the bias in the populations being compared (e.g., choosing to compare patients in the ER to other patients in the ER rather than those outside of the ER).
We further define our inclusion and exclusion criteria, then prepare the questions for participants. We choose to use a survey to ask participants in the ER about the grade of ankle sprain they had the first time they sprained their ankle. If asked the question exactly that way, participants who are in the ER with their first ankle sprain will be able to better recall the grade because that information is new and fresh. However, patients who have had multiple ankle sprains or a long time span between sprains may struggle to recall and will likely be misclassified. We can avoid this type of information bias by providing either different and larger categories for patients to pick from (e.g., “I could not walk on it” or “I needed surgery”) or even potentially selecting patients from the hospital for whom you can obtain prior records to verify their grade sprain. Either of these solutions can introduce biases of their own, making it an important decision to plan out.
5.1.2 Confounding
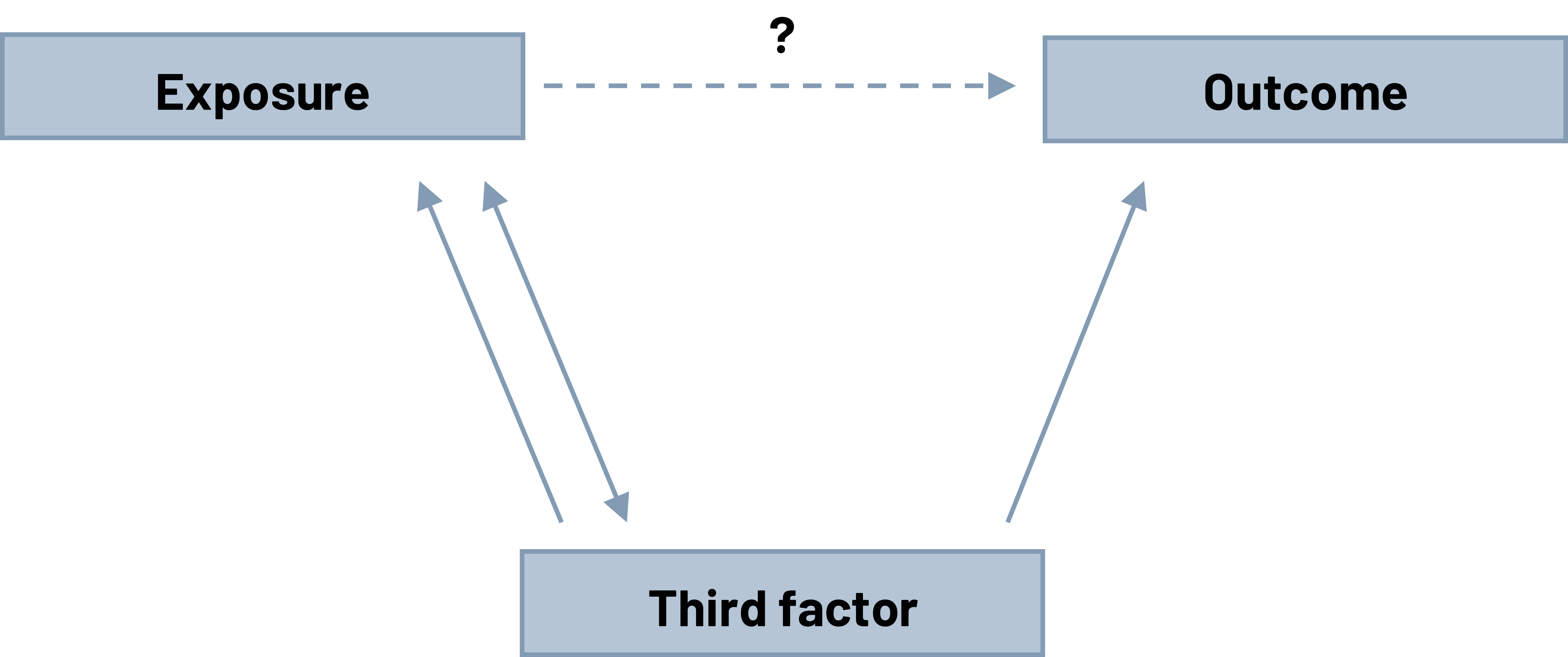
Confounding is a third factor that makes you misinterpret the relationship you see between an exposure and an outcome. The confounder is unequally distributed across the population. The type of influence it has affects everyone involved the same way.
Unlike bias, confounding is a real factor in the relationship between the exposure and the outcome. In order to be a confounder, a factor has to meet three criteria:
- It has to not be in the causal pathway. This means the exposure does not lead to this factor and then leads to the outcome.
- It has to be related to both the exposure and the outcome. The relationship to the exposure could be causal (the third factor causes the exposure) or it could be noncausal (the third factor and the exposure are related, but one doesn’t cause the other). The relationship to the outcome has to be causal (the confounder has to cause the outcome).
- The distribution of the factor among comparison groups has to be unequal. If the level of this factor was the same for everyone, there is no confounding because the influence in the two groups cannot be different (1 = 1).
Any risk factor can be a confounder but it can’t be caused by the disease, it doesn’t have to be a causal risk factor, and it has to predict the future development of the disease. How do you find confounders?
- Find a subject matter expert.
- Look at the literature.
- Think outside the box.
- Draw out all the possible causal relationships using a Directed Acyclic Graph (DAG) or the web of causation or a similar tool. Both are conceptual representations of a series of relationships.
5.1.2.1 Assessing for Confounding
You can assess (i.e., look for) the presence of confounding using a tool called stratification (figure 5.7). Stratification allows us to look at how our answer changes depending on the comparison groups. You can also use stratification to control for or adjust for (i.e., take care of) confounding. Other methods are restriction, matching, and regression. Some of the methods can be used prior to the study (design) and some can be used while you are completing your analysis.
Let’s walk through an example of how we might use stratification to see how family income influences the relationship between school sport participation and ankle sprains.
Example: Stratification
Step one of stratification is to calculate the measure of association, just as shown in chapter 3. The measure considers only the relationship between the exposure and the outcome, so it is considered to be crude or unadjusted. Let’s say we find that there is a positive relationship between school sport participation and ankle sprains (ORcrude = 3.2). Because we need to consider the effect of a third variable on this relationship, we must take that third factor into account at this point. Before we get here, we should have already made sure that this third factor even qualifies as a potential confounding variable. Our comparison groups in this example are people with family income above $100,000 a year (high) and people with a family income at or below $100,000 a year (low).
In Step two, we need to calculate the same measure of association we just calculated in step one but separately for people with a high family income (stratum # 1) and then with a low family income (stratum # 2). We find out that people with a high family income have a high odds for ankle sprain with school sport participation (ORhigh income = 4.0) but so do those with a low income (ORlow income = 3.8).
In Step three we need to compare these estimates to each other and then the crude. If we use the “eyeball method,” meaning we look to see if the numbers are about 10 percent different from each other, we can easily find out that 10 percent of 4.0 is 0.4. Is the value of 3.8 in the range of 4.0 – 0.4 and 4.0 + 0.4?
4.0 – 0.4 = 3.6
4.0 + 0.4 = 4.4
The value 3.8 is in the range of 3.6 to 4.4. We say that the stratum-specific odds ratios are similar because of this. There is a statistical test we could have used called the Breslow-Day Test, but it is beyond the scope of this text. That test can be easily calculated by most software.
We not only want to see if the stratum-specific numbers are similar to each other, we also want to see if they are similar to the crude OR. The crude OR is outside of the range we just calculated, so we know it is different than the estimate for people with high incomes.
3.8 – 0.38 = 3.42
3.8 + 0.38 = 4.18
The crude OR is also outside of the range for the estimate for people with low income. This means we can proceed to our next step. If we had found that the crude OR was similar to both stratum-specific estimates, we would stop here and say confounding is unlikely. There does not seem to be any influence of the third variable on the relationship between school sport participation and ankle sprains. However, if it was similar to one but not the other, we would still continue with our steps to assess for confounding, though perhaps with a little less confidence that it is present. Finally, if the stratum-specific measures were not similar to each other, especially if they were on opposite sides of the crude estimate, we would stop here and say that confounding is not likely, but effect modification or interaction is likely. We would ignore the crude estimate and move forward to discussing just the stratum-specific estimates.
In Step four we calculate a measure that pools together the stratum but in a way to still take into account that the groups are for high income and low income. Many times we calculate the Mantel-Haenszel (M-H) estimate (this can be for OR, RR, or other measures). In this example, we would calculate the M-H OR. This is a new version of the OR that includes all three factors. Say we find that the M-H OR in this example is 3.9.
In Step five we then compare our M-H OR to the crude OR. If they are similar, confounding is likely not present and the third factor does not influence the relationship between our exposure and outcome. If they are different, confounding likely is present, and we use only this adjusted measure from now on.
3.9 – 0.39 = 3.51
3.9 + 0.39 = 4.29
Is the crude OR of 3.2 in the range of 3.51 to 4.29? No. Because of this, we say that confounding is present. Family income confounds the relationship between school sport participation and ankle sprains. We might report this by saying there is a positive association between school sport participation and ankle sprains when adjusting for family income (M-H OR = 3.9).
5.1.3 Interaction and Effect Modification
Interaction and effect modification are similar and the terms are often used interchangeably, but they are actually very different concepts. Why do we tend to use the terms interchangeably? How are these things similar? They both refer to a third factor that influences the relationship of the exposure and outcome but is different for different people. However, there is a big difference about why the relationship is different.
- Effect modification is when the effect of the exposure on the outcome is modified by the level of a third factor (the effect modifier/control variable)
- Biological interaction
- Antagonism and synergy
- Definition is based on homogeneity and heterogeneity
- Biological interaction
- Interaction is when the observed joint effect of a risk factor and the third factor is greater than expected effect from the individual effects
- Statistical interaction
- Additive and multiplicative
- Statistical interaction
In very simple terms, the difference between effect modification and interaction is biology versus statistics. As you read journal articles, know that the terms are used interchangeably, so be careful about how you interpret the results. We use interaction and effect modification to identify differences and disparities in health outcomes between groups of people. We can find out what groups of people have a much higher risk of developing disease or having a poor outcome compared to others. Effect modification is also an important consideration in pharmacology when you consider how two drugs or treatments might interact with each other.
Example: Effect modification
Men and women can develop breast cancer. If we found out that the odds of developing breast cancer if someone lives in the United States is 8.3 (ORcrude = 8.3), we might think that everyone needed the same level of intervention. However, biology plays a role in how breast cancer develops and who it develops in. If we stratify our population by sex, we might see that people assigned female at birth have an OR of 12.3 and that those assigned male at birth have an OR of 2.5. These are very different risk profiles based on sex at birth, and they completely change how we might proceed with interventions or even simple discussions with our patients. It may affect our choice of treatment and prevention methods. If we follow our rules of stratification (section 5.1.2), we stop here and say that confounding does not appear to be present by sex but that we see effect modification. We might say that the probability of developing breast cancer is higher for people assigned female at birth that live in the United States than those that live elsewhere (ORwomen = 12.3). People assigned female at birth have a higher probability of breast cancer than people assigned male at birth, but people assigned male at birth living in the United States also have a higher probability of developing breast cancer compared to those that live elsewhere (ORmen = 2.5).
5.2 Summary
Keep bias to a minimum by setting guidelines for your study and sticking to them.
- Be careful about who you select.
- Be careful about who you compare your subjects to.
- Be careful how you collect information so you don’t misclassify.
Confounding is real. Think about all possible relationships in your data as you design and analyze your information. Failing to do so will result in erroneous conclusions. Interaction and effect modification can help us see if there are patients who will benefit from a particular therapy. If you know this exists, do not combine the groups that are different or you will have errors in analysis and interpretation.
Figure Descriptions
Figure 5.4: Three boxes form upside down triangle shape. Top left box: exposure. Top right box: outcome. Bottom center box: third factor. Third factor points to exposure and outcome. Exposure points back to third factor. Question mark above arrow that points from exposure to outcome. Return to figure 5.4.
Figure 5.5: It’s a confounding factor if…Rule #1: It is not in the causal pathway. Model crossed out with an X indicating that third factor does not influence the exposure or outcome. Rule #2: It is related to both the exposure (causally or non-causally) and the outcome (causally). Two way arrow means non-causally related. Arrow points from the thing that causes to the result! One-way arrow means causally related. Rule #3: The distribution of the factor among comparison groups is unequal. Left: bar graph that shows the third factor as skewed to be around one-third, either injured or outcome. Right: chart that shows the third factor as skewed to be around two thirds of the bar, either non-injured or no outcome. Return to figure 5.5.
Figure 5.6: Theoretical framework used to identify structural and social determinants of maternal and infant mortality in the United States. Structural determinants (slavery, GI bill, Jim Crow, 13th amendment, redlining) shape the distribution of social determinants (food stability, education, income, safety, rates of incarceration, access to care housing, neighborhood demographics). The multiple and interconnected pathways between structural and social determinants lead to increased maternal and infant mortality rates and socially defined inequities in these outcomes. Return to figure 5.6.
Figure 5.7: Step 1: Start with crude analysis (for example the OR or RR represented in 2×2 table with labels crude and OR sub crude). Step 2: Stratify (i.e., separate) the data by comparison groups (i.e., stratum). Two 2×2 tables. Left table is OR1 and stratum 1. Right table is OR2 and stratum 2. Step 3: Compare the stratum specific measures to each other using either the eyeball test (are they within 10-15% of each other?) or the Breslow-Day test. If OR1 and OR2 are not similar, stop (Effect modification/interaction likely. Report the OP for each group and do not report the crude.) If OR1 and OR2 are similar, and they are similar to crude, proceed to step 4. Step 4: Calculate an adjusted measure like the Mantel-Haenszel OR (M-H OR). Step 5: Compare the M-H OR to the crude OR. If they are similar, no confounding (Report the crude OR). If they are not similar, confounding is likely (Report the adjusted OR, the M-H OR). Return to figure 5.7.
Figure References
Figure 5.1: Possible explanations for an association between a risk factor and a disease. Adapted under fair use from USMLE First Aid, Step 1. Gianicolo EAL, Eichler M, Muensterer O, Strauch K, Blettner M. Methods for evaluating causality in observational studies. Dtsch Arztebl Int. 2020;116(7):101–107. Pannucci CJ, Wilkins EG. Identifying and avoiding bias in research. Plast Reconstr Surg. 2010;126(2):619–625. Kestenbaum B. Methods to control for confounding. In: Epidemiology and Biostatistics: An Introduction to Clinical Research. Springer New York; 2009:101–111. Corraini P, Olsen M, Pedersen L, Dekkers OM, Vandenbroucke JP. Effect modification, interaction and mediation: An overview of theoretical insights for clinical investigators. Clin Epidemiol. 2017;9:331–338.
Figure 5.2: Bias. Adapted under fair use from USMLE First Aid, Step 1.
Figure 5.3: How to check for bias in epidemiological studies. Adapted and used for noncommercial education according to IARC terms of use from IARC and dos Santos Silva I. Interpretation of epidemiological studies. In. Cancer epidemiology: principles and methods: IARC; 1999:277-303.
Figure 5.4: Definition of confounding. Kindred Grey. 2022. CC BY 4.0.
Figure 5.5: What is a confounder? Kindred Grey. 2022. CC BY 4.0.
Figure 5.6: Web of causation example of the SDOH. Adapted with permission from J. Roach, 2016. Web of Causation. CC BY NC-SA 4.0.
Figure 5.7: Stratification steps. Kindred Grey. 2022. CC BY 4.0.
- Doll R, Hill AB. Smoking and carcinoma of the lung. BMJ (Clinical research ed). 1950;2(4682):739–748. ↵
- Department of Epidemiology at the Columbia University Mailman School of Public Health, Center for New Media Teaching and Learning. Epiville: Bias Data Analysis Questions. https://epiville.ccnmtl.columbia.edu/bias/data_analysis_questions.html. Published 2022. Accessed 2022. ↵
- Department of Epidemiology at the Columbia University Mailman School of Public Health, Center for New Media Teaching and Learning. Epiville: Bias Data Analysis Questions. https://epiville.ccnmtl.columbia.edu/bias/data_analysis_questions.html. Published 2022. Accessed 2022. ↵
- dos Santos Silva I. Interpretation of epidemiological studies. In. Cancer epidemiology: principles and methods: IARC; 1999:277-303. ↵
- dos Santos Silva I. Interpretation of epidemiological studies. In. Cancer epidemiology: principles and methods: IARC; 1999:277-303. ↵

