3 Study Designs
3.1 Measurement Through Study
There are two primary categories of study designs (figure 3.1), and the primary difference between the two is whether or not we control the study factors.
In observational studies, we do not manipulate any study factors and do not randomize. We observe what happens in a particular group of people—for example, factory workers, children in a preschool, or patients seen in a clinic for primary care. When we say manipulate, we do not mean that we make things up. What we do mean is that we can set the parameters of the study (i.e., control study factors) such as who gets the exposure (e.g., a medication) or who does not (e.g., the placebo or standard of care) in order to see causal effects, if they exist between an exposure and an outcome. When we do this, it is called an experimental study.
In experimental studies, we do control factors and often use randomization to create fairly perfect conditions to see the influence of an exposure on an outcome. For example, we might enroll some cancer patients in a trial to see how a new medication works, or we might test how different the health is in communities with fluoridated water compared to those without fluoridated water. Randomization means that we use some sort of objective criteria to put study participants in whatever groups we establish for our study. For example, we may have one group that gets a sugar pill (i.e., a placebo), one group that gets the standard of care, and one group that gets the drug we are testing. In this scenario, we might assign patients to a group based on the order in which they come to the clinic. We might also choose to assign all patients a number and randomly allocate them to a group using a random number generator. No matter the assignation, we use an objective method to put patients in a study group. This helps us reduce the chance of a biased study result.
As you consider each study design, pay attention to these details:
- Number of observations made
- Directionality of exposure
- Data collection methods
- Timing of data collection
- Unit of observation
- Availability of subjects
All study designs are not created to be equal, but each has a specific purpose. Each study design helps us move closer to an understanding of causality (section 1.2). As you move from in-vitro studies to meta-analyses (figure 3.2), you can see that the evidence each study design provides becomes stronger. It does not mean the designs at the top are weaker or useless, they just provide a different type of evidence. Though there is a general consensus about how valid or strong the evidence is from any particular type of study, the evidence from each design builds on the others.
| Study types | |
|---|---|
| In-vitro | Least strong information. Just as important as the study types below.* |
| Animal research | |
| Anecdotes, opinions, ideas | |
| Case reports, case series | |
| Ecologic study | |
| Cross-sectional | |
| Case control | |
| Cohort | |
| Community trials | |
| Randomized control trials (RCT) | |
| Systematic reviews | |
| Meta-analyses | Strongest information. Just as important as the study types above.* |
| *All study types are important and each level builds on the ones before it. | |
Figure 3.2: How much can we rely on the answers from your study when determining the etiology (cause) of disease or conditions?
Example: Types of study designs
What happens when we approach the same topic and question with different study designs? Let’s find out using osteoarthritis as an example.
- In vitro: In vitro models for the study of osteoarthritis
- Animal: Animal models of osteoarthritis: classification, update, and measurement of outcomes
- Opinion: Current opinion: where are we in our understanding and treatment of osteoarthritis?
- Case report: The effect of knee resizing illusions on pain and swelling in symptomatic knee osteoarthritis: a case report
- Cross-sectional: Is There an Association Between a History of Running and Symptomatic Knee Osteoarthritis? A Cross-Sectional Study From the Osteoarthritis Initiative
- Case control: A case-control study to investigate the relation between low and moderate levels of physical activity and osteoarthritis of the knee using data collected as part of the Allied Dunbar National Fitness Survey
- Cohort: Running does not increase symptoms or structural progression in people with knee osteoarthritis: data from the osteoarthritis initiative
- RCT: Ultrasound-Guided Injection of Platelet-Rich Plasma and Hyaluronic Acid, Separately and in Combination, for Hip Osteoarthritis: A Randomized Controlled Study
- Systematic review: Is Participation in Certain Sports Associated With Knee Osteoarthritis? A Systematic Review
- Meta-analysis: Is Participation in Certain Sports Associated With Knee Osteoarthritis? A Systematic Review
In the real world, study designs are not always clearly distinguishable from each other. There often is overlap such as that seen in the nested case-control, cross-sectional case-control, and case-cohort study designs.
3.2 Study Designs
Beyond the measures presented in chapter 2, epidemiologic studies allow us to create and compare measures across individuals and groups. Because we are really examining the relationship between factors, exposures, and outcomes, we call the majority of these measures of association. Figures 3.3 and 3.4 lay out the different types of studies and some overview details about them. The rest of this chapter is dedicated to explaining and discussing temporality, measures of association, measures of effect, and sampling.
Figure 3.3 describes five types of observational study designs: case series, ecologic studies, cross-sectional studies, case-control studies, and cohort studies. From left to right, the designs are listed in order of the strength of their evidence (weakest to strongest).
| Details | Observational designs (in order of strength) | ||||
|---|---|---|---|---|---|
| Case series | Ecologic | Cross-sectional | Case control | Cohort | |
| Also known as | Case study | Correlational study | Prevalence study | Case-referent study | Follow-up study |
| Descriptive or analytic? | Descriptive | Primarily descriptive | Descriptive | Analytic | Analytic |
| Can temporality be determined? | No | No | No | No | Yes |
| Unit of observation | Individual | Group | Individual | Individual | Individual |
| Major uses of the design/What is the design good for? | Describe interesting cases of disease, injury, or other health issues. | Test or develop etiologic hypotheses (hypotheses about the population). Create hypotheses about causation or identify methods of prevention. | Present the burden of disease, injury, or other health issues (morbidity or mortality). Generate hypotheses. Supports planning health services. | Outbreaks, studying diseases of low prevalence, testing hypotheses. | Studying etiology, providing direct measures of risk, testing hypotheses, showing temporal relationships, looking at rare exposures. |
| What measures or measures of association are used with the design? | None | Correlation, chi-square | Prevalence estimates, prevalence rate ratio (AKA prevalence relative risk) | Odds ratio | Relative risk (most often), odds ratio (sometimes) |
| Formula | N/A | Depends on the design | (Uses prevalence not incidence like the RR) |
This cross-product ratio is the derivative of: |
(Direct Measurement of Risk)
(Indirect Measurement of Risk) This cross-product ratio is the derivative of: |
| Advantages | Able to share information with others to then develop hypotheses or plan studies. | Quick and easy to conduct. Inexpensive. | Sometimes quick and relatively easy to conduct (if using secondary vs primary data). Inexpensive. | Great with rare outcomes. Cheap, efficient. Can be completed rather quickly. | Great with rare exposures. Can show temporal relationships between exposure and disease retrospectively, prospectively, or a combination of the two. |
| Disadvantages | Not enough details to make decisions for treatment. | Ecologic fallacy. Imprecise measurement. | Not good for rare diseases. Shouldn’t be used for etiologic studies. | Not good for rare exposures. Cannot provide a direct measure of risk. Recall bias. | Can cost a lot of money and take a lot of time to complete. Difficult to execute. Selection bias. Not good for rare diseases. |
| Example | We had five patients with hallucinations after taking NSAID A that is not known for causing hallucinations. We will describe their clinical presentation here. | The rate of premature births decreased in West Virginia when Medicaid was expanded. | The prevalence of high adiposity increased in New Mexico during the COVID-19 pandemic amongst people 60 to 65 years of age that were retired. | People that worked in grocery stores during the first four months of the COVID-19 pandemic were more likely to be hospitalized with COVID-19 than the general population. | Soldiers that entered boot camp in 1980 and stayed in the military for 20 years had a higher risk of osteoarthritis at 60 than soldiers that entered at the same time and stayed in the military less than 7 years. |
| PRR: Prevalence Rate Ratio OR: Odds Ratio RR: Relative Risk |
|||||
Figure 3.3: Epidemiological study designs.
Figure 3.4 describes two types of experimental study designs: community trials and clinical trials.
| Details | Experimental designs | |
|---|---|---|
| Community trial | Clinical trial | |
| Also known as | Community intervention study | RCT |
| Descriptive or analytic? | Analytic | Analytic |
| Can temporality be determined? | Yes | Yes |
| Unit of observation | Community | Individual |
| Major uses of the design/What is the design good for? | Useful for seeing how effective community-level interventions are, evaluating policies, or implementing healthier behaviors in the community. | Useful for testing efficacy of new medications, therapies, treatments, or preventative methods (such as vaccines). If a multiphase trial, the steps are: Can I swim? Phase 0: Initial efficacy work (pharmacodynamics and pharmacokinetics) Phase I: Safety assessment Phase II: Does it work? Phase III: Does it lead to any improvement in the condition? Phase IV: Are there any issues that require us to pull it off the market? |
| Formula | Depends on the design | Depends on the design |
| Advantages | Randomization of communities. Researchers can sometimes manipulate the exposure. Can establish causality. | Randomization of subjects. Can manipulate exposure. Can control everything else. Can set up as a cross-over trial (same group of participants serves as both the cases and the controls). Can establish causality. |
| Disadvantages | Hard to control everything such as people moving in and out of the study area. Impossible to make everyone in the area participate. | The fact everything is controlled means it is uncertain whether it will work the same way in the real world. |
| Example | Communities with fluoridated water have better oral health outcomes than communities without fluoridated water. | Drug B is more efficacious at reducing atrial fibrillation than standard of care during a phase III trial. |
Figure 3.4: Community trials and clinical trials.
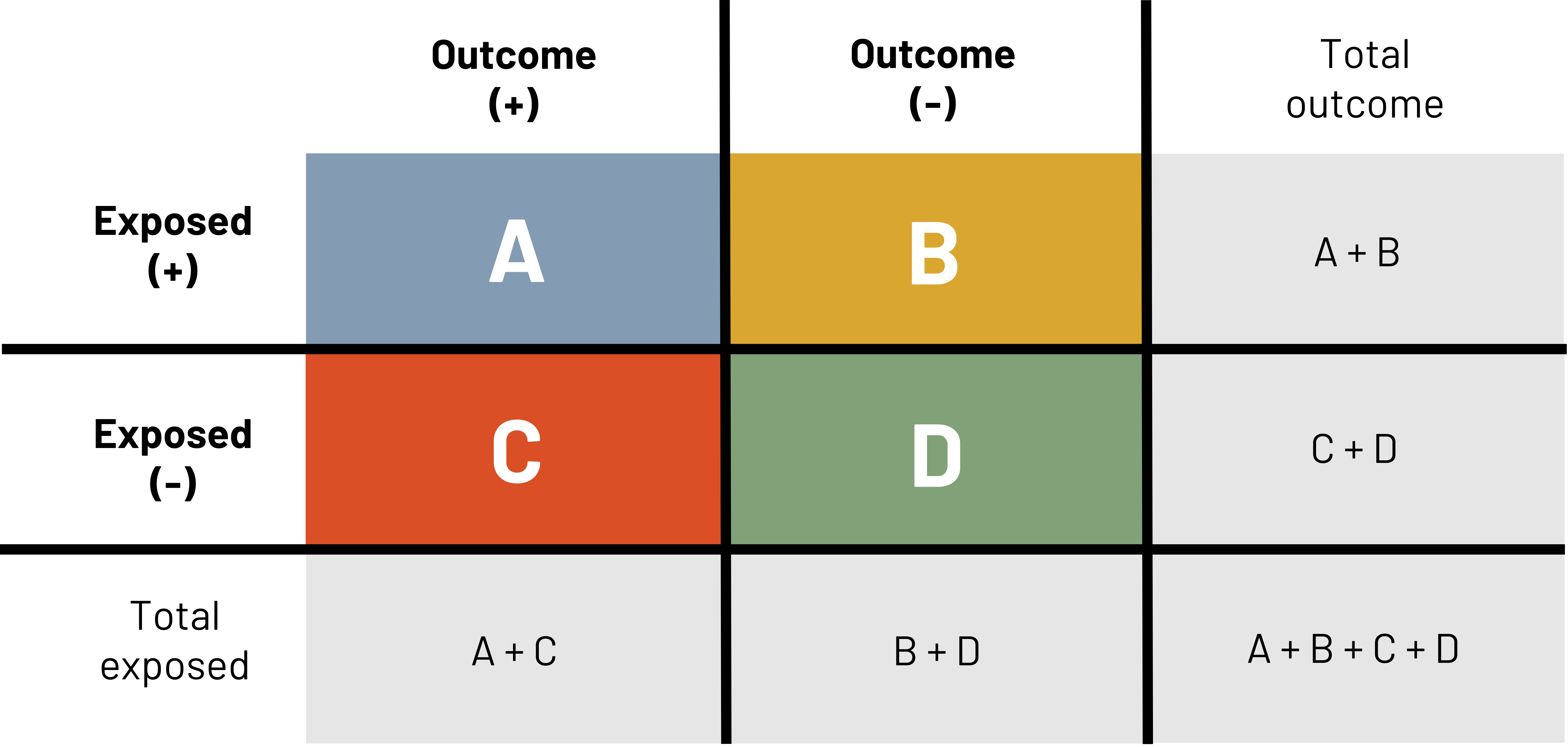
One tool that is used to calculate a number of epidemiological measures is the 2×2 table (figure 3.5). This table is repeated many times in the following text. The primary columns represent the presence (e.g., outcome +) or absence (e.g., outcome –) of the outcome or event of interest (e.g., ACL injury). The primary rows represent the presence (e.g., exposed +) or absence (e.g., exposed –) of the exposure of interest (e.g., being hit). In this example table we also show the total number of those exposed and the total number of those with the outcome. These totals are sometimes needed for different calculations.
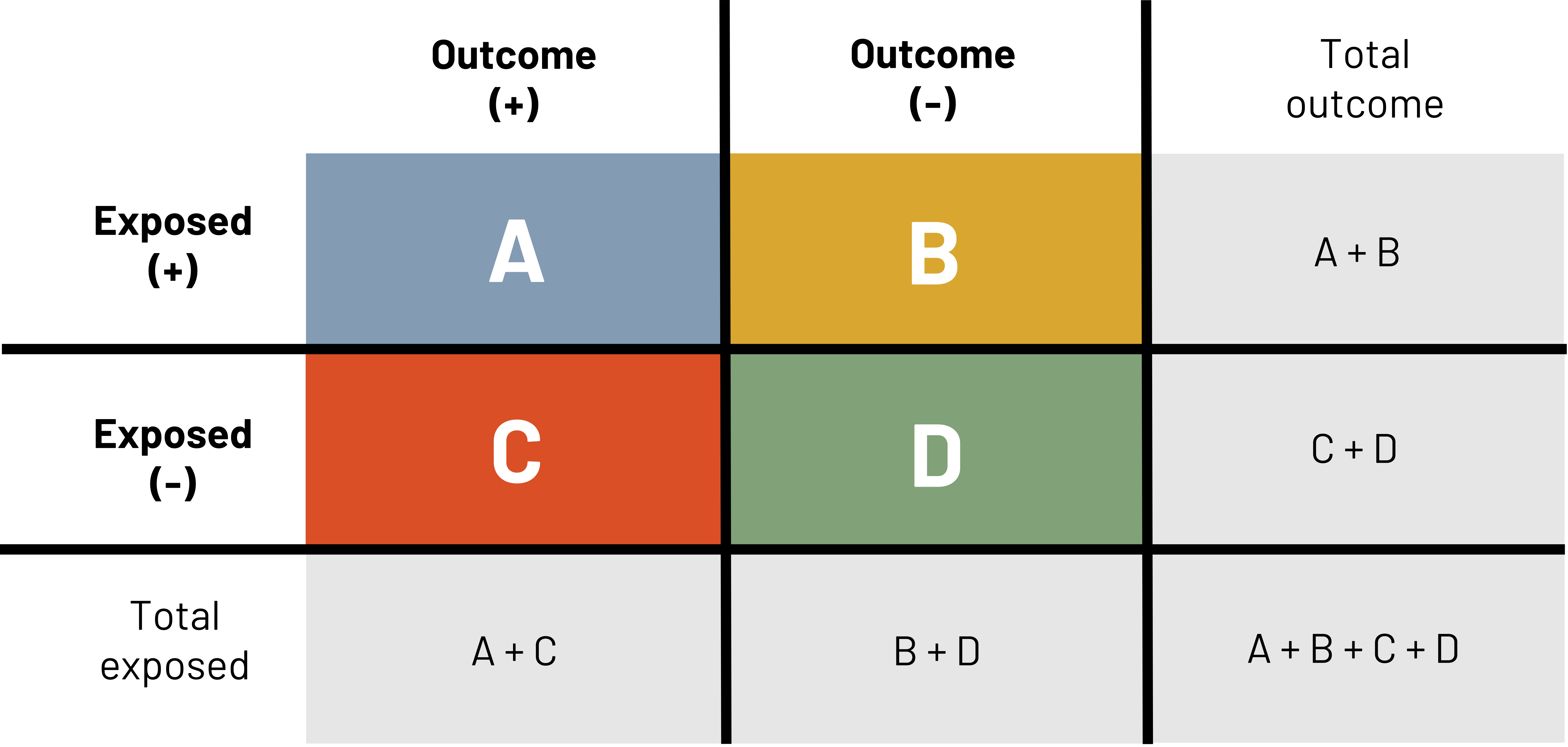
The letters A, B, C, and D represent the number of observations that meet different criteria.
A = The count of observations that have both the outcome and the exposure
B = The count of observations that have the exposure but not the outcome
C = The count of observations that have the outcome but not the exposure
D = The count of observations that have neither the outcome nor the exposure
Using this same logic, the sum of A and B gives us the total number of observations with the exposure and the sum of C and D gives us the total number of observations without the exposure. The sum of A and C gives us the total number of observations with the outcome and the sum of B and D gives us the total number of observations without the outcome.
3.3 Temporality
In order to establish causality, it is important to be able to establish a temporal—or time—relationship between factors. As seen in figures 3.3 and 3.4, all studies are not good at measuring temporality. All studies also are not intended to measure temporality. Studies such as cohort studies or RCTs are the most used when trying to answer questions such as “Did the chicken come first or did the egg?” [Answer to that question![1]]. Figure 3.6 displays at what point in time data collection for different studies starts, the directionality of data collection, and the minimum number of time points captured by the study. For example, in a cross-sectional study all data is captured at the same point in time (the present day) and shows what is happening right now. Cross-sectional studies can be thought of as a snapshot in time, and the time period could vary from something such as a patient’s last visit to patient outcomes over the last year. Because all questions get asked at once and typically involve recalling events from the past, we cannot determine temporality. A cross-sectional study can, however, give us a great perspective about the prevalence of a particular health issue. A retrospective cohort study, on the other hand, starts in the present day but looks backwards to capture information from the past. Oftentimes, there can be confusion about the difference between a retrospective cohort study and a case-control study. Even in a retrospective cohort study, our goal is to determine if a known exposure leads to a disease, such as when we are trying to determine whether playing football leads to developing chronic traumatic encephalopathy (CTE). We have information about the population both before and after diagnosis, which allows us to observe whether the exposure led to the disease. In a case-control study, we are looking to find what exposures could have led to known disease. It is most often used when we need an answer quickly, such as in an outbreak; for example, what caused an outbreak of ringworm in wrestlers. While we start with people we know have the outcome, we have to determine what possible exposures are of interest and then narrow down which one had the higher probability of causing the outcome. We cannot definitively determine temporality. One of the main differences between a prospective cohort study and a randomized control trial is that instead of seeing the natural course of exposure (e.g., choice to smoke or not smoke), we instead randomly allocate participants into our study groups—we choose for them. This means we may give one group the standard of care for an ankle injury and give the other group a new cryotherapy plus standard of care to see the effect the cryotherapy has on the outcome of the injury.
3.4 Observational Study Designs
Ecological studies use group summary measures for exposure and outcome rather than measures about individual people. We would use this type of study to compare populations, such as the rate of disease in France compared to the United States or the rate of disease in the United States in 1950 compared to 2000. Because this type of study compares groups, we cannot assume that the results from this study should apply to individuals. It also means that studies we do using data on individuals should not be assumed to apply to groups. If we were to do that, we would be committing the ecologic fallacy.
Example: Ecologic fallacy
If we find out that the rate of heat-related illnesses during track and field is high in states in the southern United States, that does not automatically mean that individuals in the southern United States have higher risks of heat-related illness than people living other places. It just means that on a group basis, their rates are higher. If we find out that 80 of 100 individual people with heat illness at a track meet are from the southern United States, it does not mean that 80 percent of all heat-related illnesses occur in the southern United States. If we do make these incorrect assumptions, we have just been guilty of the ecological fallacy. We need to do a better job being correct in our inferences, or the meaning we assign to the data that we see. It would be a fallacy to assume that people from the southern United States will experience heat illness based on the presentation of data.
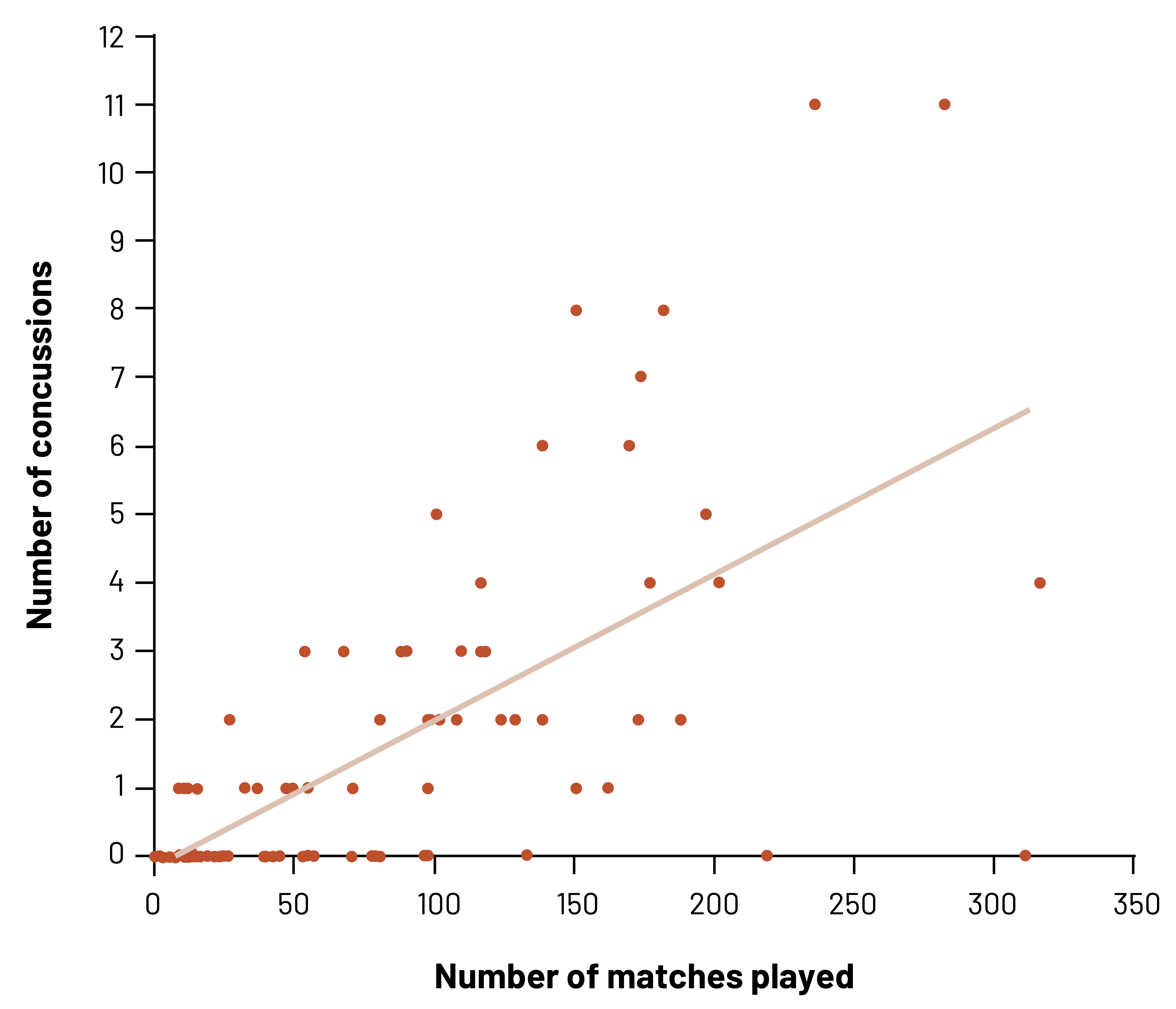
In this example, we see that there is a positive relationship between the number of Professional Australian Football matches played and the number of concussions that were diagnosed.[2] However, we would not want to assume that every player with more matches will have any concussions. As we can see, at least some players with a high number of matches have no concussions. We also can see that some players with few matches have a higher number of concussions than players with more matches. We can only infer what we see, which is the probability (chance) of an increased risk of concussion with more matches.
In a 2006 TED Talk, statistics expert and physician Hans Rosling provided an excellent example of the importance of ecological studies. You can see it in the first 7 minutes of this video.[3]
Cross-sectional studies measure the prevalence of disease and of exposures (i.e., risk factors) at one point in time. Cross-sectional studies are also known as prevalence studies. When we think about what is being measured in a cross-sectional study, we should think about taking a photo or a snapshot: it is a photo of you right now, not what you looked like in the past or what you will look like in the future. We do not know when an exposure happened or when a disease started, we just know they are present right now.
Example: Cross-sectional study
During the COVID-19 pandemic, professional athletes in the United States needed to pass cardiac testing in order to return to play after testing positive for COVID-19. Researchers conducted a study to find out the “prevalence of detectable inflammatory heart disease” among athletes in the National Basketball Association, the Women’s National Basketball Association, National Hockey League, National Football League, Major League Soccer, and Major League Baseball between May and October 2020.[4] They found that 789 athletes tested positive for COVID-19 and, of those, 30 required further screening.[5] Ultimately, 5 athletes had detectable inflammatory heart disease and were held out of play.
Case-control studies are used to find out whether a particular exposure could have been the source or cause of a disease, particularly in urgent health situations. We start by identifying who already has the disease (cases), then we find a set of people who are like the cases in every respect except they do not have disease. These are called controls. We ask these cases and controls questions about their past exposures. Because we start with people who are diseased, case-control studies are great when you are interested in studying people who have rare diseases. This design is explored more in the next section on Outbreak Investigations.
Cohort studies start with a group of individuals based on their exposure status. They are used to find out whether a particular disease comes after a particular exposure or development of a risk factor. If someone does not have the chance of being exposed, they would not be a good selection for a cohort study. You want everyone to have the potential of getting the outcome because of the exposure. Because of this, cohort studies are great when you’re interested in studying people who have rare exposures. Once the exposure status is identified, researchers then identify whether or not the subjects have the outcome of interest already. If they do, they would be removed from a prospective study because our goal is to see if the outcome happens after the exposure, and if they already have both, how would we know? There are roughly three types of cohort studies: prospective, retrospective, and historical. Every cohort study has at least two data collection points and they do not overlap. Prospective means we are setting up the study today and actively following forward into the future. Retrospective means we are setting up the study today but we are looking at information that was previously gathered. So how are retrospective cohort studies different from case-control studies? (See figure 3.6.)
In our next example, we explore how we might approach hospital-acquired infections after anterior cruciate ligament (ACL) reconstruction surgery compared to ACL repair surgery with a cohort study or a case-control study.
Example: Hospital-acquired infections after ACL reconstruction surgery vs ACL repair surgery
Type of question that can be answered with retrospective cohort study: We are interested in identifying whether there are more hospital-acquired infections (the outcome) after ACL reconstruction surgery compared to ACL repair surgery (the exposure).
In a retrospective cohort study, we would start by identifying everyone in the population under study (e.g., all patients seen at hospital A) who was eligible for ACL surgery using hospital records. We would select from this population people who had either the ACL reconstruction or ACL repair surgery at Hospital A. We then go through their records to identify what happened to them prior to having the surgery and then move forward through their records to see whether they developed a hospital-acquired infection after surgery. Measurement 1: Eligibility for study (exposure status) and determination of whether they already had the outcome before the surgery (which would exclude them). Measurement 2: Determination of whether they had the outcome after the surgery. This provides evidence that the hospital-acquired infection came after the surgery but doesn’t rule out that it could have been caused in full or in part by something else postsurgically.
Type of question that can be answered with case-control study: Hospital A has a number of hospital-acquired infections after surgery. We are interested in identifying whether ACL reconstruction surgery or ACL repair surgery is more common (exposure) in people who have hospital-acquired infections (cases).
In a case-control study, we would start by identifying everyone in the population under study (e.g., all patients seen at hospital A) who had a hospital-acquired infection after surgery (the outcome) using hospital records. We would find patients in Hospital A who did not have the hospital-acquired infection but could have gotten it from surgery (controls). We would then use existing records or talk to patients/providers/environmental services to find out more info about the potential places in the hospital where they could have gotten the infection. This would have helped us identify the type of surgery as a potential exposure. We would compare the cases with the exposure (e.g., ACL reconstruction surgery) to those without the exposure to see if there was a difference in the chance of having a hospital-acquired infection. Whatever exposures have the higher OR would be the ones we’d investigate further as the potential place to intervene. Measurement 1: Eligibility for study, exposure status, disease status. No second measurement.
3.5 Measures of Association
As noted in section 3.2, we often use a 2x2 table to analyze data from an epidemiological study (figure 3.5). This table is repeated many times in the following text.
Beware! While one side of the table above has exposure (or risk factors) and the other side has outcomes (such as disease), everyone does not set their table up the same way (see figure 3.10). Before doing any calculations with data from a 2x2 table, pay attention to how it is set up. All examples in this book use the version showing exposure in rows and outcome in columns.
When we calculate our measures of association, we refer to the needed components by referring to different boxes of our 2x2 table using letters.
- A – Has the outcome and is exposed
- B – Does not have the outcome and is exposed
- C – Has the outcome and is not exposed
- D – Does not have the outcome and is not exposed
Examples of the measures of association are the odds ratio and the relative risk. A measure used in cross-sectional studies is the prevalence rate ratio.
| Study design | Measures of disease | Measures of risk | Temporality |
|---|---|---|---|
| Ecological | Prevalence (rough estimate) | Prevalence ratio | Retrospective |
| Proportional mortality | • Proportional mortality • Standardized mortality |
• Proportional mortality ratio • Standardized mortality ratio |
Retrospective |
| Case-crossover | None | Odds ratio | Retrospective |
| Cross-sectional | • Point prevalence • Period prevalence |
• Odds ratio • Prevalence odds ratio • Prevalence ratio • Prevalence difference |
Retrospective |
| Case-control | None | Odds ratio | Retrospective |
| Retrospective and prospective cohort | • Point prevalence • Period prevalence • Incidence |
• Odds ratio • Prevalence odds ratio • Prevalence ratio • Prevalence difference • Attributable risk • Incidence rate ratio • Relative risk • Risk ratio • Hazard ratio |
• Retrospective only • Both retrospective and prospective • Prospective only |
Figure 3.11: The variety of measures that can be calculated from different study designs.
3.5.1 Odds Ratio
The only measure of association that can be calculated in a case-control study is the odds ratio (OR) [the probability of being exposed among cases compared to the probability of being exposed among controls]. This particular odds ratio is referred to as the odds ratio of exposure.
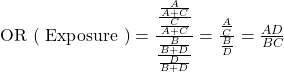
![]() is the ratio of those with the outcome and exposure (A) to those with the outcome but no exposure (C). In other words, what proportion of those that have the outcome have the exposure?
is the ratio of those with the outcome and exposure (A) to those with the outcome but no exposure (C). In other words, what proportion of those that have the outcome have the exposure?
![]() is the ratio of those without the outcome but with the exposure (B) to those without the outcome and with no exposure (D). In other words, what proportion of those that do not have the outcome have the exposure?
is the ratio of those without the outcome but with the exposure (B) to those without the outcome and with no exposure (D). In other words, what proportion of those that do not have the outcome have the exposure?
The shortcut, ![]() , is called the cross-product ratio.
, is called the cross-product ratio.
![]()
The resulting answer is a direct comparison of the ratio of the proportion of those with the exposure who have the outcome to proportion of those with the exposure without the outcome. If this number is equal to 1 (roughly, 0.9 to 1.1), there is no difference in the probability of having the exposure between the outcome groups. If this number is greater than 1 (roughly, greater than 1.1), the group with the outcome is more likely to have the exposure than the group without the outcome. If this number is less than 1 (roughly, less than 0.9), the group with the outcome is less likely to have the exposure than the group without the outcome.

Always be specific when drawing comparisons. Just saying, for example, “Cases are 3.2 times more likely to have the exposure” is an incomplete interpretation of the OR. “Cases are 3.2 times more likely to have the exposure compared to controls” is clear about what you are comparing the odds of cases to. This applies to relative risk interpretations as well.
We can also calculate an OR (of exposure or disease) in other study designs, including cross-sectional, cohort, and RCTs. How it gets interpreted in these cases is often different than how we interpret it in a case-control based on the nature of the study and the difference in the full calculation.
3.5.2 Relative Risk
The primary measure of association that is calculated in a cohort study is the relative risk (the risk or incidence of the outcome in the exposed compared to the risk or incidence of the outcome in the unexposed).
![]() is the incidence (or risk) of disease (A) in the exposed (A+B).
is the incidence (or risk) of disease (A) in the exposed (A+B). ![]() is the incidence (or risk) of disease (C) in the unexposed (C+D). The relative risk is the ratio of the incidence of disease in the exposed to the incidence of disease in the unexposed. In other words, how is the risk of disease in the exposed different than the risk of disease in the unexposed?
is the incidence (or risk) of disease (C) in the unexposed (C+D). The relative risk is the ratio of the incidence of disease in the exposed to the incidence of disease in the unexposed. In other words, how is the risk of disease in the exposed different than the risk of disease in the unexposed?
If this number is equal to 1 (roughly, 0.9 to 1.1), there is no difference in the risk between exposure groups. If this number is greater than 1 (roughly, greater than 1.1), the group with the exposure is more likely to have the disease than the group without the exposure. If this number is less than 1 (roughly, less than 0.9), the group with the exposure is less likely to have the disease than the group without the exposure.

Calculating the odds ratio in a cohort study means that we are calculating the odds ratio of disease. This is calculated differently than the odds ratio of exposure that we calculate in a case-control study (see above). While both formulas result in the cross-product ratio, because they were calculated differently we interpret them differently. Remember that cohort studies are to identify the risk of disease in the exposed compared to the risk of disease in the unexposed.
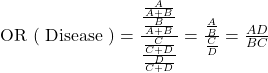
3.5.3 Prevalence Rate Ratio
As noted earlier, prevalence is:
![]()
In cross-sectional studies, a common measure of association we calculate is the prevalence rate ratio. While the name is a misnomer (prevalence is a proportion, not a rate), it still uses a familiar formula to compare things like the prevalence between either two separate groups (e.g., injury prevalence in Oklahoma compared to injury prevalence in Texas) or the same group at different points in time (e.g., injury prevalence in Virginia in 2015 compared to injury prevalence in Virginia in 2020).
![]()
![]()
3.6 Outbreak Investigations
An outbreak is the occurrence of disease in an area at a level exceeding the normally expected number of cases. An outbreak technically differs from an epidemic because an outbreak occurs in a more limited geographic area. Epidemics are declared by country-specific health bodies (e.g., the US Centers for Disease Control and Prevention). A disease is endemic if it is occurring at a level expected. It is normally occurring in that place. An epidemic becomes a pandemic when the World Health Organization decides it has become one. A pandemic is an epidemic that is spread over multiple countries or continents. Epidemics and pandemics can have variable time patterns, as seen in section 2.4.
One of the most common ways that outbreaks are identified is through clinicians paying attention to changes in what they are treating and who they are treating. Figure 3.14 displays the 11 steps to solving an outbreak.[6]

Step 1: Establish the existence of an outbreak.
Step 2: Verify the diagnosis.
Before we expend too many resources and too much time, we want to be sure that we are actually observing an outbreak. Things that could look like an outbreak but are not:
- Misdiagnosis/false report:
- False positive (specificity)
- Laboratory error
- Change in case definition
- Incorrect time or place
- False report
- Changes in:
- Awareness
- Record keeping
- Observation
- Population composition
Sometimes we improve our surveillance systems or other tracking methods and pick up more cases because we are doing a better job. This does not mean we actually have more cases, we just are doing a better job at seeing them. Other times, we simply make mistakes in identification that could make it appear like we have more cases. Besides these things, we start calculating our prevalence and incidence, as well as if there are reasonable explanations for changes in these numbers, to determine whether to proceed. We should calculate prevalence if we need to know the total burden of the problem. We should calculate incidence if we are trying to find the risk of developing a disease in a given time. Sometimes we need to do both. The most important part of steps 1 and 2 is that we must verify that the diagnosis we think is the problem is in fact the correct diagnosis. For example, if we think that we are having an outbreak of meningitis A, we should confirm that all of the people who are sick actually have meningitis A.
Our goal is to identify all of the following:
- Individual: Who is affected?
- Place: Where are they affected?
- Time: When did this start or change?
- Connections: What factors are related?
Moving forward in an outbreak investigation is all about what we think, what we know, and what we can prove.
Step 3: Construct a working case definition.
Taking this information, we move into Step 3 and create a working case definition. Many times, this definition stays in flux. Using our case definition, we identify the individual cases, controls, and possible/suspected cases.
Case definitions include a standard set of criteria used to determine if an individual should be classified as a case. Depending on the condition or disease in question, case definitions may already be established. In other situations, this needs to be developed as the investigation progresses. Sometimes the disease or condition in question is required to be reported to the health department or the Centers for Disease Control and Prevention. Nationally notifiable conditions are reported to the National Notifiable Diseases Surveillance System.[7] Each state also has a separate list of notifiable conditions. For example, Virginia’s conditions are reported to the Virginia Department of Health and the State Board of Health.[8]
A case definition usually includes both:
- Clinical criteria and/or lab test
- Restrictions by time, place, and/or person
When developing the case definition, we tend to emphasize sensitivity (to identify all possible cases) over specificity (to identify only “true” cases). Part of this is because it is better to err with caution and include too many people than not all cases, especially in the beginning of the investigation. Sensitivity and specificity are discussed in more detail in chapter 4.
Example: Case definition
In figure 3.15, we see the diagnostic criteria for hemophagocytic lymphohistiocytosis (HLH), a rare syndrome of excessive immune response. In order to be considered someone who has HLH, a person must have most but not all diagnostic criteria. However, sometimes not all patients will have all tests that are required to be considered a case. If they meet several criteria, they are instead what is known as a possible or probable case.

Step 4: Find cases systematically and record information.
Once we have a case definition, we can then work to find all cases (Step 4). We must do this in a systematic fashion and record data on any cases or potential cases we find. We make every effort to find cases that occurred earlier than when we first realized something might be amiss. We use a line listing to organize the data about our cases. In figure 3.16, we see an example of a line listing from an anthrax outbreak. Each row corresponds to a different case, and we include all the possible details relevant to the case status and demographic information.
| Case no. | Onset date, 2001 | Date of anthrax diagnosis by lab testing | State | Age (years) | Sex | Race | Occupation | Case status | Anthrax presentation | Outcome | Diagnostic tests |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9/22 | 10/19 | NY | 31 | F | W | NY Post employee | Suspect | Cutaneous | Alive | Serum IgG reactive |
| 2 | 9/25 | 10/12 | NY | 38 | F | W | NBC anchor assistant | Confirmed | Cutaneous | Alive | Skin biopsy IHC+/ Serum IgG reactive |
| 3 | 9/26 | 10/18 | NJ | 39 | M | W | USPS machine mechanic | Suspect | Cutaneous | Alive | Serum IgG reactive |
Figure 3.16: Example line listing.
Step 5: Perform descriptive epidemiology.
In Step 5, we perform descriptive epidemiology on the data we have gathered from clinical records, questionnaires, interviews, and so on. Just as with several other conditions, if it is a suspected foodborne outbreak, we can use tools from CDC[9] to gather all the pertinent details. We are specifically looking for patterns and associations between risk factors and disease. All the information we will compare is in our line listing. Our measures of association and effect are very useful at this step.
If it is a foodborne outbreak, instead of calculating incidence as we learned before, we usually reframe risk as the attack rate (figure 3.17).
![]()
We can use this to find what percentage of those at risk are actually ill.
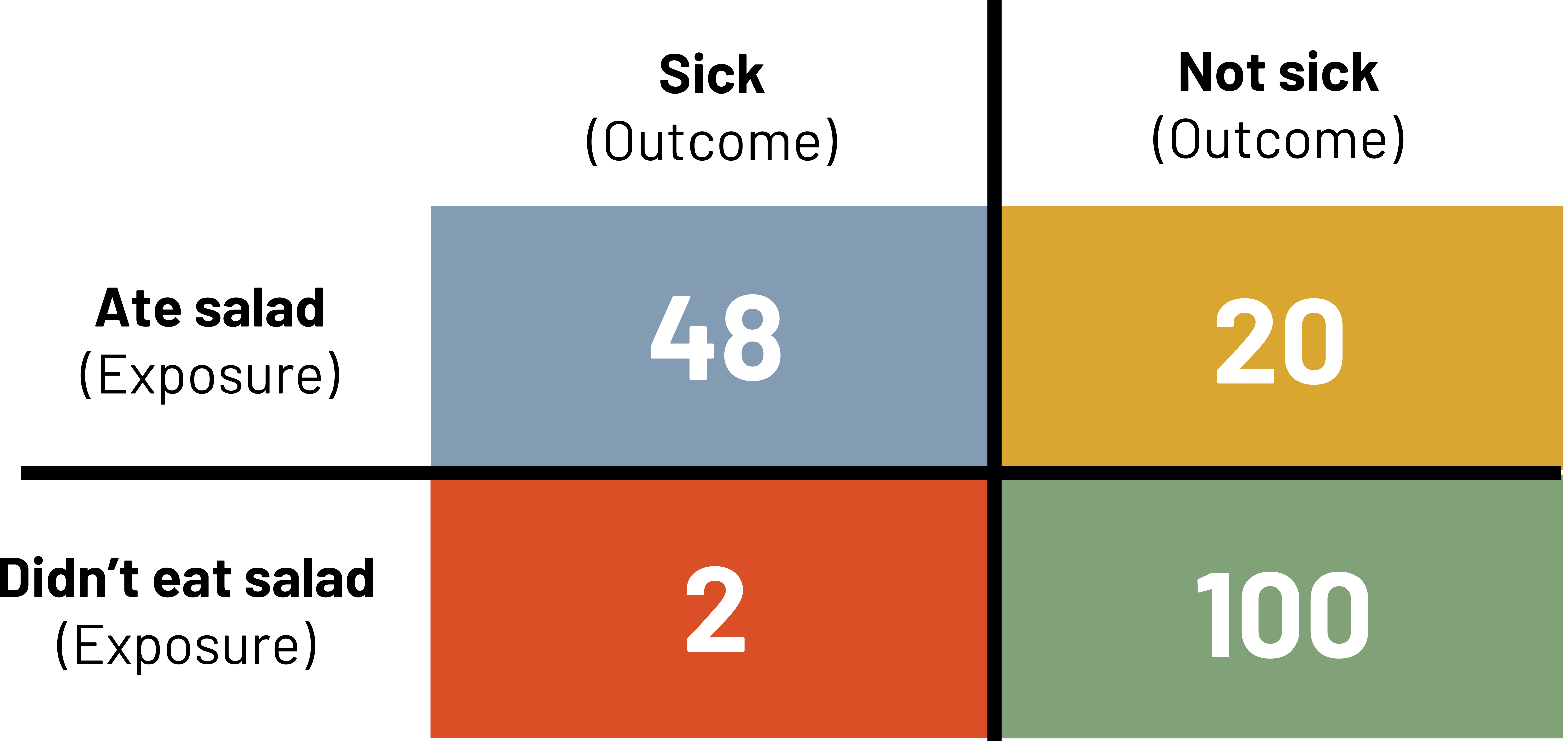
![]()
We interpret the attack rate as the percentage of those with the exposure that are sick. In the above example, 70.6 percent of those that ate salad are sick. We would compare attack rates to determine which exposures deserve more attention as possible causes.
Step 6: Develop hypotheses.
Step 7: Evaluate hypotheses epidemiologically.
In Steps 6 and 7, we form hypotheses based on our existing data and test them. Among other things, our hypotheses may relate to:
- Cause of the outbreak
- Risk factors for disease
- Risk factors for infection
- Intervention to stop spread: quarantine and vaccinate
- Treatment of affected individuals
Step 8: As necessary, reconsider, refine, and reevaluate hypotheses.
Step 9: Compare and reconcile with laboratory and/or environmental studies.
Step 10: Implement control and prevention measures.
Step 11: Initiate or maintain surveillance findings.
Our final steps of an outbreak investigation are to continue refining our hypotheses, compiling more data to support or refute our hypotheses, controlling the outbreak, and performing surveillance to keep an eye on the problem. Sometimes we find the source of the problem but cannot just “solve” it. The cost of treating the problem, the cost of the intervention to fix the problem, and the existence of other alternatives all play into our decision about what to do. Controlling the problem might include vaccine development and distribution, it might be stopping access to a dangerous substance, or recalling food products.
In the case of some problems, like COVID-19 or sickle cell disease, we initiate and maintain an ongoing systematic data collection system. This is known as disease surveillance. The US Centers for Disease Control and Prevention reports on the surveillance of notifiable diseases in both the Morbidity and Mortality Weekly Report[10] (MMWR) and CDC WONDER.[11]
3.7 Measures of Effect
When we are comparing results from our study, we compare the measures that we found. Often, we look at:
-
- How big is the difference between groups or individuals with and without a particular risk factor? (Magnitude of effect; ratio, difference)
- Could the difference we found be just due to chance variation? (Significance of effect; p values)
- How certain are we of the size of the effect? (Precision of, or uncertainty in, estimate; confidence intervals)
We specifically discuss A in this book. More details on B and C can be found in many books on biostatistics.
We already looked at whether one factor was associated with (or related to) another factor or whether an outcome was associated with an exposure. But in the grand scheme of things, what does that really mean for the population we are focused on?
Measures of effect (how big is the effect of an exposure or risk factor) include the attributable risk (attributable fraction) and the population attributable risk (population attributable fraction). Sometimes epidemiologists and others will refer to these as more measures of association rather than separating them into their own category. Because they are very interrelated, it does not matter whether you refer to them as measures of effect or measures of association but rather when and how to use them. When we’re focused on population health, looking at relative differences like the odds ratio or relative risk is extremely useful to decide where we want to make a difference and what factors we should spend our time and energy on. But when we’re trying to figure out how to approach the problem at the individual level (for your patient for example), absolute measures can be much more useful.
3.7.1 Attributable Risk
Of everyone that has the exposure, how much of the occurrence of the disease is due to the exposure in question? That’s the attributable risk. In other words, what’s the difference in how much disease we could already expect without the exposure (risk in the unexposed) and how much disease we have if the exposure is present (the risk in the exposed)? This could also be called the risk difference. The risk in the unexposed is often referred to as the baseline risk.
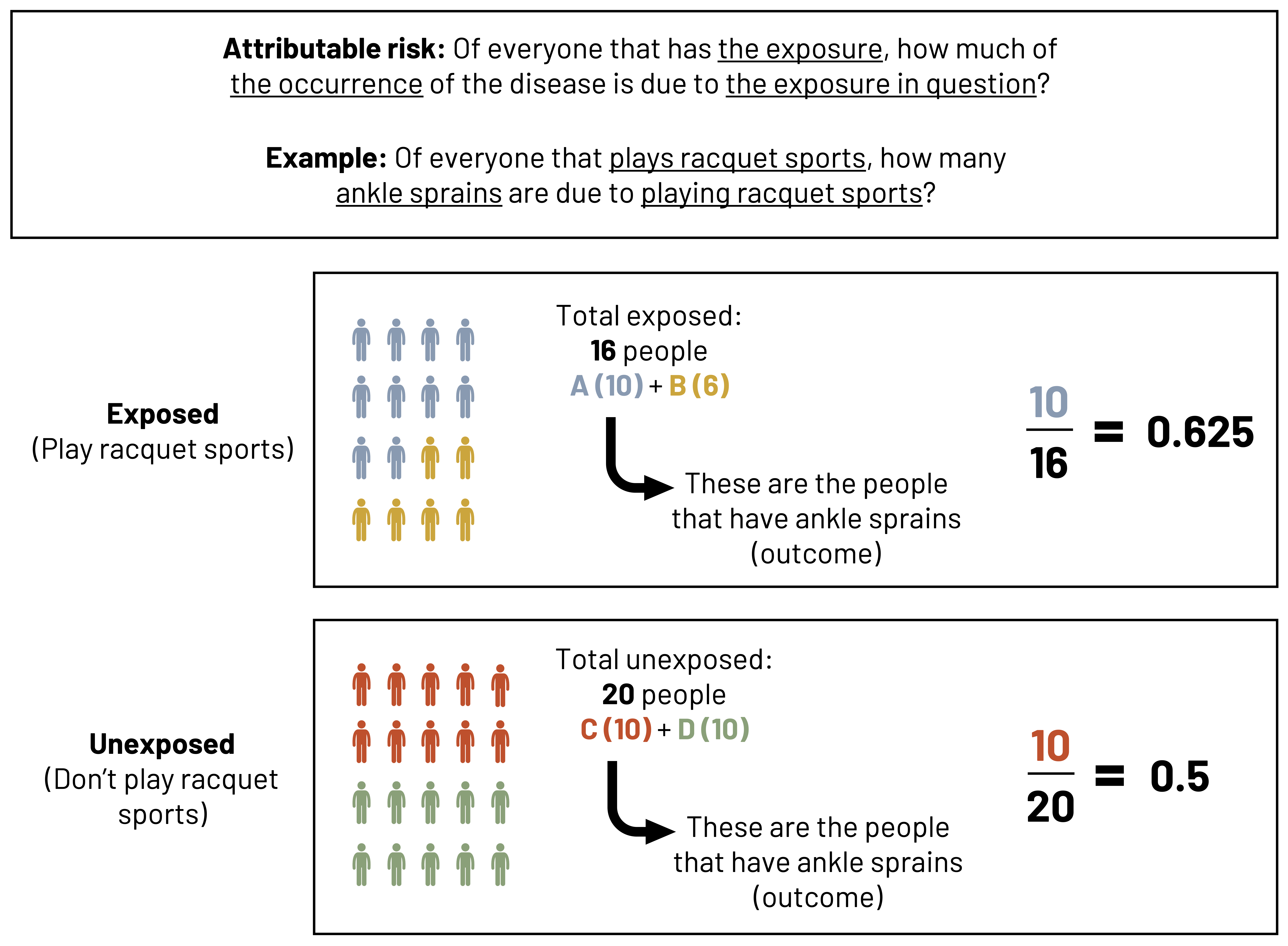
In our example, the risk of disease in the exposed group is ![]() (0.625). The risk of disease in the unexposed group is
(0.625). The risk of disease in the unexposed group is ![]() (0.500). The attributable risk is the difference between these two numbers:
(0.500). The attributable risk is the difference between these two numbers:
AR = 0.625 - 0.500 = 0.125
The number we get—0.125—is called an absolute number that tells us how different the risk is for the exposed than the risk for the unexposed. For improved understanding, we tend to make it relative by turning it into a percentage.
![]()
![]()
The AR percent tells us what percent of the risk of disease in the exposed group is attributable to the exposure itself. In this case, 20 percent of the risk of an ankle sprain in those that play racquet sports is due to those people playing racquet sports.
When we use attributable risk to see how well a clinical intervention (e.g., a vaccination) performs, we know that the relative risk correlates to how well the intervention will perform. If the relative risk is < 1 (lower risk of the outcome due to the intervention), then the AR will be negative. This is what happens if the intervention works! If the relative risk is > 1 (higher risk of the outcome due to the intervention), then the AR will be positive. This is what happens when the intervention is not that great.
Further reading
Check out this article on the use of the risk difference and the relative risk when comparing the effectiveness of treatment options.[12]
3.7.2 Measures Especially Important in Clinical Medicine
If we can figure out the attributable risk, we can also identify the relative risk reduction, the absolute risk reduction, the number needed to treat, and the number needed to harm.
| Measure | Equation | Which way to round |
|---|---|---|
| Relative risk reduction (RRR) | - | |
| Absolute risk reduction (ARR) | Neither. Take the absolute value. | |
| Number needed to treat (NNT) | Up | |
| Number needed to harm (NNH) | Down |
Figure 3.20: Summary of important clinical medicine measures.
The relative risk reduction: If there is a reduction in the risk of the outcome when a particular intervention is used, how much of that is due to the intervention compared to the control?
![]()
The absolute risk reduction (also known as the risk difference): While the ARR and the AR can both be referred to as the risk difference, there is a distinct difference between the two. AR refers to the difference in risk for the outcome among the exposed due to the exposure itself. The ARR is broader and refers to the difference in risk for the outcome in the group that did not have the intervention and the risk for the outcome in the group that did have the intervention.
![]()
Note
Remember that the vertical bars mean that we take the absolute value of anything between them. So mathematically, | -3 | is equal to 3. We should remember that the difference was negative, so we can take that into account later.
The number needed to treat: How many patients have to be treated in order to make a difference for one patient?
![]()
Always round the result of the NNT formula up.
The number needed to harm: How many patients have to be exposed to a risk factor in order to harm one patient?
![]()
Always round the result of the NNH formula down.
These four measures (NNH, NNT, ARR, and RRR) are very important in clinical medicine.[13] Figure 3.22 provides an example of how to calculate these statistics.
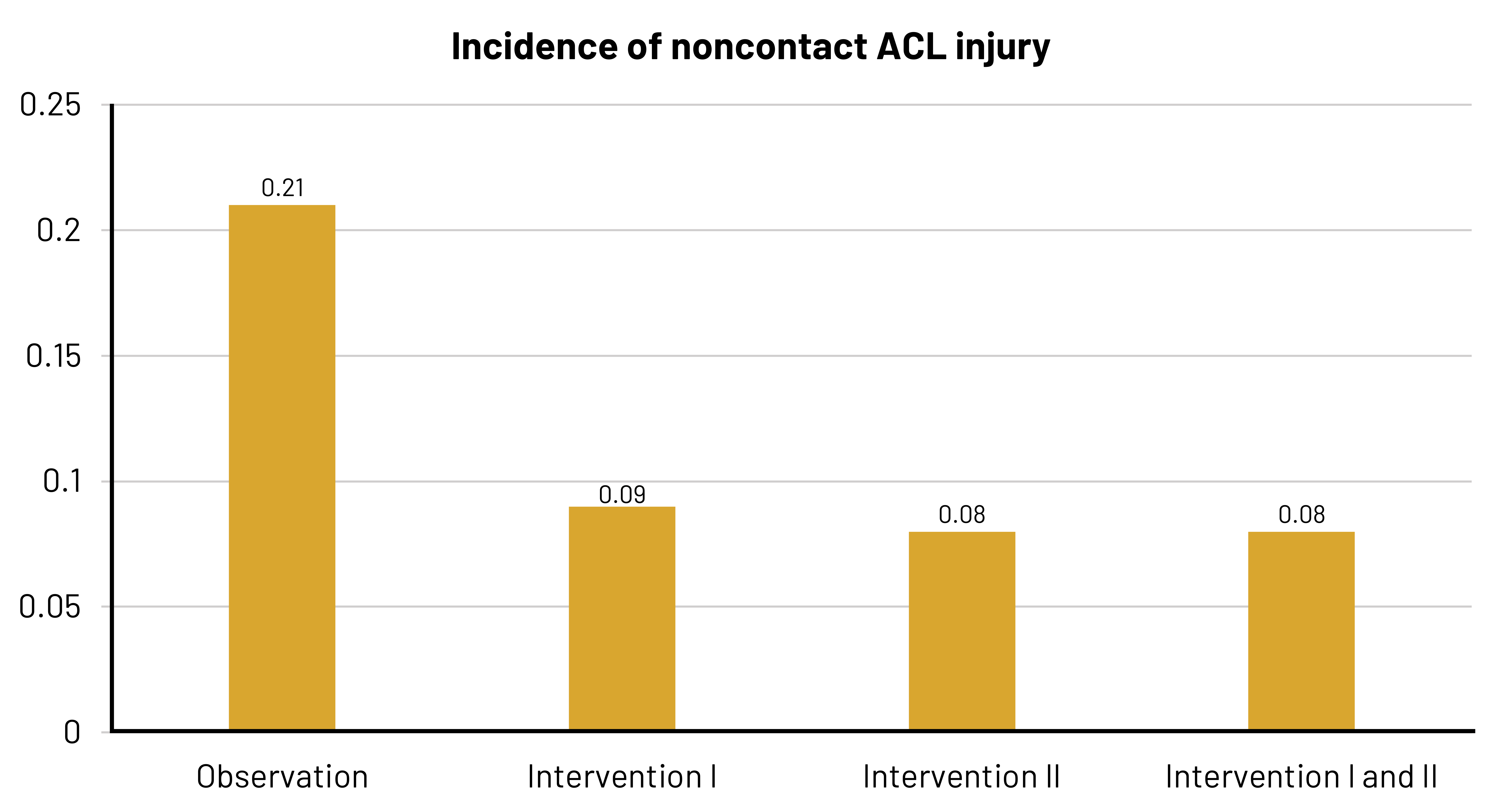
Female athletes have a greater risk for ACL injury than male athletes for a variety of reasons. Some 70 percent of ACL injuries in female athletes are due to reasons other than coming in contact with an object or a person. Basketball players are at risk for ACL injury due to the movements they make during play. A study was conducted by Omi et al.[14] to identify the effectiveness of an intervention that aimed to alter risk factors like landing mechanics, muscular strength, postural control, and hip joint control.
The graphic shown (figure 3 from the manuscript[15]) shows the following rates:
- Incidence rate of noncontact ACL injury for 309 athletes who did not receive an intervention (the initial observation period) [Total of 13 injuries]
- Incidence rate for 268 athletes who received Intervention I (players used a ball to simulate basketball rebounding motions and worked to have appropriate knee alignment during landing) [Total of five injuries]
- Incidence rate for 268 athletes who received Intervention II (an upgrade to Intervention I that included [a] application of a flexible band at the thigh level in all jump-landing maneuvers except for contact jump to reduce hip adduction, hip internal rotation, and knee valgus; [b] implementation of hip external rotation strengthening in addition to hip abduction strengthening; and [c] enhancement in quality of balance exercises such as cross-leg hop forward and side hop) [Total of three injuries]
- Combined incidence rate for Interventions I and II
If you need more numbers to follow along, download the manuscript17 from PubMed. Remember that rounding differently and using the rates per 1000 athlete-exposures (aka, person-time) as opposed to incidence per total in the group results in differences in numbers during calculations.
For the purpose of our example, we’ll refer only to the Observation, Intervention I, and Intervention II parts of the graphic.
- Risk of noncontact ACL injury during Observation = 0.21
- Risk of noncontact ACL injury during Intervention I = 0.09
- Risk of noncontact ACL injury during Intervention II = 0.08
How much of the risk of noncontact ACL injury during Intervention I is due to participating in Intervention I?
If we are comparing Intervention I to the Observation (which can be considered baseline since no intervention has taken place):
Relative risk = ![]() = 0.43
= 0.43
Athletes who participate in Intervention I have 0.43 times the risk of a noncontact ACL injury compared to athletes at baseline. Intervention I seems to reduce the risk of noncontact ACL injury.
Attributable risk (risk difference) = 0.09 – 0.21 = -0.13
Our risk difference is negative. The risk of a noncontact ACL injury is reduced by 13 percent in those who participate in Intervention I.
Relative Risk Reduction = 1 – 0.43 = 0.57
The intervention reduces the risk of noncontact ACL injuries by 57 percent.
Absolute Risk Reduction = ![]() –
– ![]() = 0.04 – 0.02 = 0.025
= 0.04 – 0.02 = 0.025
The intervention reduces the risk of noncontact ACL injury 2.5 percent compared to baseline.
Number Needed to Treat = ![]() = = 40
= = 40
To prevent a noncontact ACL injury in just 1 athlete, 40 athletes must participate in the intervention.
Number Needed to Harm = N/A [There is a positive NNT, so there is no NNH for Intervention I]
If we are comparing Intervention II to the Observation:
Relative risk = ![]() = 0.38
= 0.38
Athletes who participate in Intervention II have 0.38 times the risk of a noncontact ACL injury compared to athletes at baseline. Intervention II seems to reduce the risk of noncontact ACL injury.
Attributable risk (risk difference) = 0.08 – 0.21 = -0.14
Our risk difference is negative. The risk of a noncontact ACL injury is reduced by 14 percent in those who participate in Intervention II.
Relative Risk Reduction = 1 – 0.38 = 0.62
The intervention reduces the risk of noncontact ACL injuries by 62 percent.
Absolute Risk Reduction = ![]() –
– ![]() = 0.03
= 0.03
The intervention reduces the risk of noncontact ACL injury 3 percent compared to baseline.
Number Needed to Treat = 1/0.03 = 34
To prevent a noncontact ACL injury in just 1 athlete, 34 athletes must participate in the intervention.
Number Needed to Harm = N/A [There is a positive NNT, so there is no NNH for Intervention II]
Both the relative risk of noncontact ACL injury after Intervention I and after Intervention II are less than half the risk of noncontact ACL injury when no intervention was used. Intervention II had a slight improvement over Intervention I for how much it reduced the risk of noncontact ACL injury when comparing the absolute risk reductions vs baseline (3 percent vs 2.5 percent).
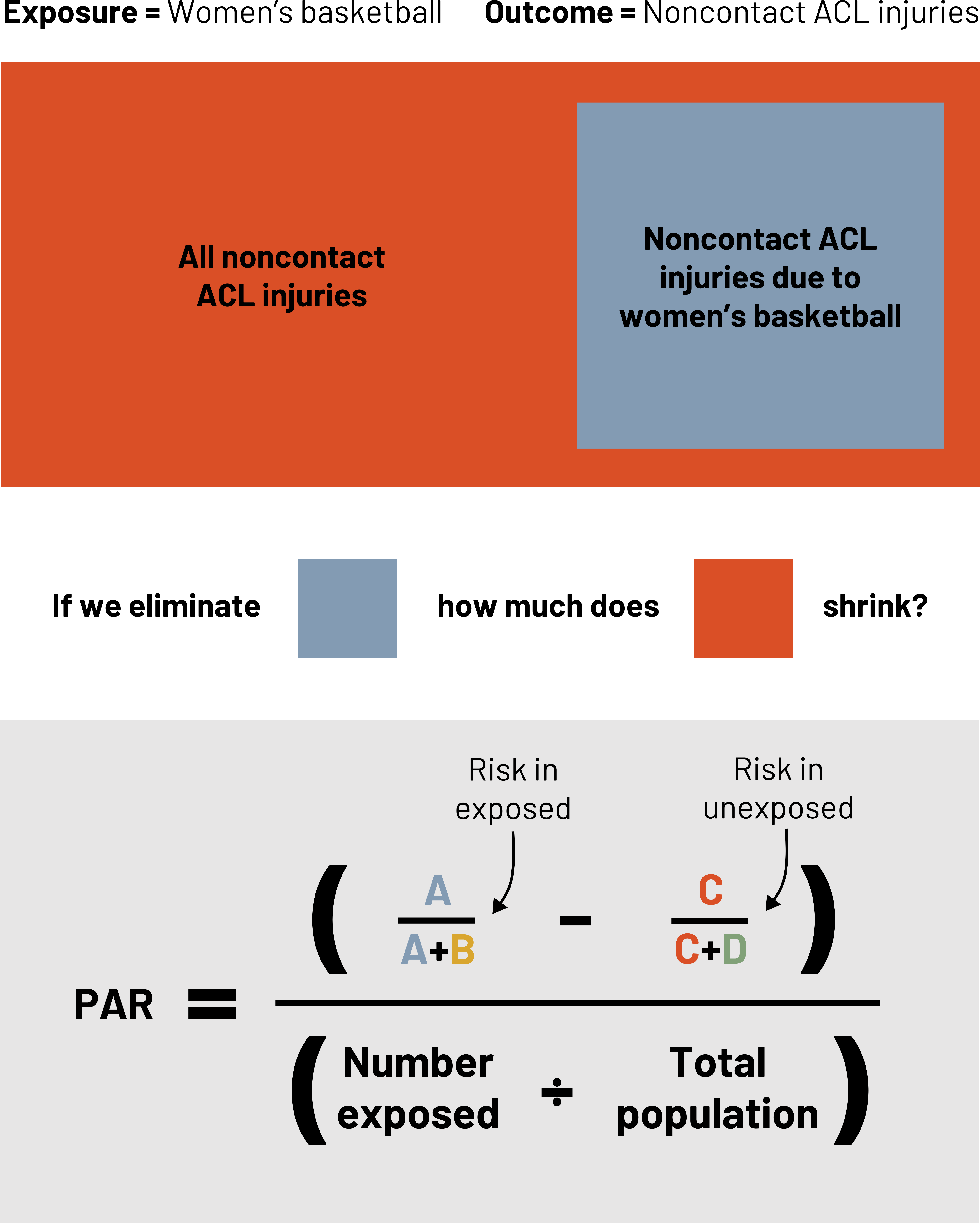
Attributable risk and its derivatives are important when we are considering a specific population, but often when we develop medications or create other interventions we are considering how much impact they will have on the overall burden of a health problem. Extending our example (figure 3.22), how many noncontact ACL injuries could we have eliminated from the entire population if we eliminated them from women’s basketball? The answer to this question is the population attributable risk. The population attributable risk is the absolute level of risk of the outcome in the whole population due to the exposure. The difference between this and the attributable risk is that this applies to the risk reduction even in those that do not have the exposure. One way to calculate this is:
Example: Population attributable risk
Say there are 4500 NCAA women’s basketball players. Based on our example data for Intervention I:
![]()
![]()
Just like the AR, it can be easier to understand this as a percentage.
![]()
![]()
![]()
By implementing Intervention II among all NCAA women’s basketball players, we would reduce the total burden of noncontact ACL injuries in this population by less than 1 percent. This intervention may work well on an individual level but not as a population level intervention for noncontact ACL injuries.
Further reading
Want to dive deeper into how the ARR and the RRR should (and shouldn't) be used in real life?
Here’s a great explanation related to how not to confuse the public with the COVID-19 vaccination.[16]
Here's a helpful video on how to calculate the NNT.[17]
Interested in why you need the RR to calculate the AR?[18]
Here's an article on how to use risk difference, risk ratio, and odds ratio in clinical medicine.[19]
3.8 Reporting Results of Epidemiologic and Clinical Studies
There are various standards for the reporting of study results and methods. Figure 3.24 provides an example list of different standards. You can find additional standards for various disciplines and different types of studies at the EQUATOR network website.[20]
| Standard name | Acronym | Website |
|---|---|---|
| Consolidated standards of reporting trials | CONSORT | www.consort-statement.org |
| Strengthening the reporting of observational studies in epidemiology | STROBE | www.strobe-statement.org |
| Standards for reporting studies of diagnostic accuracy | STARD | http://dx.doi.org/10.1136/bmjopen-2016-012799 |
| Quality assessment of diagnostic accuracy studies | QUADAS | www.bris.ac.uk/quadas |
| Preferred reporting items for systematic reviews and meta-analyses | PRISMA | www.prisma-statement.org |
| Consolidated criteria for reporting qualitative research | COREQ | https://doi.org/10.1093/intqhc/mzm042 |
| Statistical analyses and methods in the published literature | SAMPL | https://doi.org/10.1016/j.ijnurstu.2014.09.006 |
| Consensus-based clinical case reporting guideline development | CARE | www.care-statement.org |
| Standards for quality improvement reporting excellence | SQUIRE | www.squire-statement.org |
| Consolidated health economic evaluation reporting standards | CHEERS | https://doi.org/10.1136/bmj.f1049 |
| Enhancing transparency in reporting the synthesis of qualitative research | ENTREQ | https://doi.org/10.1186/1471-2288-12-181 |
Figure 3.24: Standards for study design and reporting.
In addition to reporting study results, it is also normal and helpful to report on how studies were designed and implemented. This reporting of methods helps others better understand all the work that goes into obtaining results as well as potential roadblocks to watch out for when designing a similar study to expand what is known about a topic. The CARE Consortium published a journal article in 2017 about how they built a national study of concussion in service academy students and collegiate athletes with the Department of Defense.[21]
Figure Descriptions
Figure 3.1: Flow chart. Following pathway to left: Controlled assignment of subjects to study conditions arrow to randomized (clinical trials) or non-randomized/quasi-experimental (community trials). Clinical trials and community trials are types of experimental studies. Following pathway to right: Uncontrolled/not randomized assignment of subjects to study conditions, arrow to sampling with regard to exposure, characteristic, or cause (prospective studies). Sampling with regard to disease or effect, arrow to time of exposure/characteristic. Exposure or characteristic at time of study (cross-sectional studies). History of exposure or characteristic prior to time of study (retrospective studies). Prospective studies, retrospective studies, and cross-sectional studies are types of observational studies. Return to figure 3.1.
Figure 3.5: Headers on top of table are outcome (+) and outcome (-). Headers to left of the table are exposed (+) and exposed (-). If outcome (+) and exposed (+), A. If outcome (-) and exposed (+), B. If outcome (+) and exposed (-), C. If outcome (-) and exposed (-), D. Reading left to right in the table: A, B, C, D. Outside of the table are calculations for finding total exposed and total outcome. Below the table left to right: total exposed, A+C, B+D, A+B+C+D. Right of the table top to bottom: total outcome, A+B, C+D, A+B+C+D. Total population represented by A+B+C+D in bottom right corner. Return to figure 3.5.
Figure 3.6: Cross-sectional study (natural allocation): in the present, risk factor (+) and risk factor (-) point to compare disease prevalence. Case-control study (natural allocation): in the present, controls without disease and diseased cases both point to past box stating compare risk factor frequency. Retrospective study (natural allocation): in the past, risk factor (+) and risk factor (-) point to present box stating compare disease incidence; another box in present time states review previous records with a dotted arrow pointing back to the past risk factors. Prospective cohort study (natural allocation): in the present, risk factor (+) and risk factor (-) point to future box stating compare disease incidence. Randomized control trial (random allocation): in the present, risk factor (+) and risk factor (-) point to future box stating compare disease incidence. Return to figure 3.6.
Figure 3.7: X-axis displays number of matches played (ranging from 0 to 350). Y-axis displays number of concussions (ranging from 0 to 12). Roughly 50 data points on the graph with a regression line indicating the average. As number of matches played increases, the number of concussions increases. Return to figure 3.7.
Figure 3.8: Cohort study: study population is disease-free and at-risk. Half of the study population is labeled cohort 1 (exposed group), the other half is labeled cohort 2 (unexposed group). Of the cohort 1 group, there are some with disease and some with no disease. Of the cohort 2 group, there are some with disease and some with no disease. Diseased status in two cohorts is identified. Case control study: there are separate groups based on outcome status. First group: cases (outcome present). Second group: controls (outcome absent). Each of these groups have subgroups where there is either a present exposure or an absent exposure. Return to figure 3.8.
Figure 3.9: Headers on top of table are outcome (+) and outcome (-). Headers to left of the table are exposed (+) and exposed (-). If outcome (+) and exposed (+), A. If outcome (-) and exposed (+), B. If outcome (+) and exposed (-), C. If outcome (-) and exposed (-), D. Reading left to right in the table: A, B, C, D. Outside of the table are calculations for finding total exposed and total outcome. Below the table left to right: total exposed, A+C, B+D, A+B+C+D. Right of the table top to bottom: total outcome, A+B, C+D, A+B+C+D. Total population represented by A+B+C+D in bottom right corner. Return to figure 3.9.
Figure 3.10: Three separate 2x2 tables. First: Outcome (-) and outcome (+) are above the table and exposure (-) and exposure (+) are left of the table. Second: exposure (+) and exposure (-) are above the table and outcome (+) and outcome (-) are left of the table. Third: exposure (-) and exposure (+) are above the table and outcome (-) and outcome (+) are left of the table. Return to figure 3.10.
Figure 3.12: OR < 1 (e.g., 0.9): exposure less likely in those with outcome compared to those without the outcome. OR = 1: no difference. OR > 1 (e.g., 1.1): exposure more likely in those with outcome compared to those without the outcome. Return to figure 3.12.
Figure 3.13: RR < 1 (e.g., 0.9): disease less likely in the exposed group compared to those that are unexposed. RR = 1: no difference. RR > 1 (e.g., 1.1): disease more likely in the exposed group compared to those that are unexposed. Return to figure 3.13.
Figure 3.14: 1: Establish the existence of an outbreak. 2: Verify the diagnosis. 3: Construct a working case definition. 4: Find cases systematically and record information. 5: Perform descriptive epidemiology. 6: Develop hypotheses. 7: Evaluate hypotheses epidemiologically. 8: As necessary, reconsider, refine, and re-evaluate hypotheses. 9: Compare and reconcile with laboratory and/or environmental studies. 10: Implement control and prevention measures. 11: Initiate or maintain surveillance findings. Steps 8-11 often happen simultaneously. Return to figure 3.14.
Figure 3.15: 1: familial disease/known genetic defect. 2: clinical and laboratory criteria (5/8 criteria should be fulfilled). Criteria: fever, splenomegaly, cytopenia greater than or equal to 2 cell lines (hemoglobin less than 90 g/l or less than 120 g/l if below 4 weeks of age, platelets less than 100 x 10^9/l, neutrophils less than 1 x 10^9/l), hypertriglyceridemia and/or hypofibrinogenemia (fasting triglycerides greater than or equal to 3 mmol/l, fibrinogen less than 1.5 g/l), ferritin greater than or equal to 500 mu g/l, soluble IL-2 receptor 25 greater than or equal to 2400 U/ml, decreased or absent natural killer cell activity, hemophagocytosis in bone marrow, cerebrospinal fluid, or lymph nodes. Supportive evidence is cerebral symptoms with moderate pleocytosis and/or elevated protein, elevated transaminases, bilirubin, lactate dehydrogenase. Return to figure 3.15.
Figure 3.17: 2x2 table. Above table labels: sick (outcome) and not sick (outcome). Left table labels: ate salad (exposure) and didn't eat salad (exposure). A: 48 (sick and ate salad). B: 20 (not sick and ate salad). C: 2 (sick and didn't eat salad). D: 100 (not sick and didn't eat salad). Return to figure 3.17.
Figure 3.18: Above the table is outcome (+) and outcome (-). Left of the table is exposed (+) and exposed (-). If outcome (+) and exposed (+), A. If outcome (-) and exposed (+), B. If outcome (+) and exposed (-), C. If outcome (-) and exposed (-), D. Reading left to right in the table: A, B, C, D. Outside of the table are calculations for finding total exposed and total outcome. Below the table left to right: total exposed, A+C, B+D, A+B+C+D. Right of the table top to bottom: total outcome, A+B, C+D, A+B+C+D. Additional rightmost column: risk. A/(A+B) and C/(C+D). Return to figure 3.18.
Figure 3.19: Attributable risk: Of everyone that has the exposure, how much of the occurrence of the disease is due to the exposure in question? Example: Of everyone that plays racquet sports, how many ankle sprains are due to playing racquet sports? Example follows. Total exposed (play racquet sports): 16 people (A=10 and B=6). A represents people that have ankle sprains (outcome). A (10) divided by total exposed (16) equals 0.625. Total unexposed (don't play racquet sports): 20 people (C=10 and D=10). C represents people that have ankle sprains (outcome). C (10) divided by total unexposed (20) equals 0.5. Return to figure 3.19.
Figure 3.21: Three boxed columns with steps for calculations of relative risk reduction, number needed to treat, and number needed to harm based on relative risk. If risk in exposed is smaller than baseline, AR is negative. If risk in exposed is larger than baseline, AR is positive. Left column: When relative risk is equal to one, the baseline risk and risk in exposed are equal. Calculating RR: 4 (risk in exposed) divided by 4 (baseline risk) equals an RR of 1. Calculating AR: 4 (risk in exposed) minus by 4 (baseline risk) equals an AR of 0. Calculating ARR: absolute value of 4 (baseline risk) minus 4 (risk in exposed) equals an ARR of 0. Middle column: When relative risk is greater than one, the baseline risk is smaller than the risk in exposed. Calculating RR: 5 (risk in exposed) divided by 3 (baseline risk) equals an RR of 1.667. Calculating AR: 5 (risk in exposed) minus 3 (baseline risk) equals an AR of 2. Calculating ARR: absolute value of 3 (baseline risk) minus 5 (risk in exposed) equals an ARR of 2. Right column: When relative risk is less than one, the baseline risk is larger than the exposed. Calculating RR: 2 (risk in exposed) divided by 7 (baseline risk) equals an RR of 0.286. Calculating AR: 2 (risk in exposed) minus 7 (baseline risk) equals an AR of -5. Calculating ARR: absolute value of 7 (baseline risk) minus 2 (risk in exposed) equals an ARR of 5. Return to figure 3.21.
Figure 3.22: Bar chart showing incidence of noncontact ACL injury. Incidence on x-axis and rates on y-axis. Observation: 0.21. Intervention one: 0.09. Intervention two: 0.08. Intervention one and two: 0.08. Return to figure 3.22.
Figure 3.23: Exposure = women's basketball. Outcome = Noncontact ACL injuries. Noncontact ACL injuries due to women's basketball is a small subset of all noncontact ACL injuries. If we eliminate the small subset, how much does the all noncontact ACL injuries category shrink? Population attributable risk (PAR) equals (risk in exposed minus risk in unexposed) divided by (number exposed divided by total population). Risk in exposed = A divided by (A+B). Risk in unexposed = C divided by (C+D). Return to figure 3.23.
Figure References
Figure 3.1: Overview of study designs. Kindred Grey. 2022. Adapted under fair use from Lilienfeld AM. Advances in quantitative methods in epidemiology. Public Health Rep. 1980;95(5):462–469.
Figure 3.2: Bhopal RS. The concept of risk and fundamental measures of disease frequency: Incidence and prevalence. In: Bhopal, RS. Concepts of epidemiology: Integrating the ideas, theories, principles and methods of epidemiology. Oxford University Press; 2008:201–234.
Figure 3.3: Epidemiological study designs. Adapted under fair use from USMLE First Aid, Step 1.
Figure 3.4: Community trials and clinical trials. Adapted under fair use from USMLE First Aid, Step 1.
Figure 3.5: Example 2x2 table. Kindred Grey. 2022. CC BY 4.0.
Figure 3.6: Temporality. Kindred Grey. 2022. CC BY 4.0.
Figure 3.7: Ecological relationship between concussion incidence and matches played. Kindred Grey. 2022. CC BY 4.0. Data from Gibbs N, Watsford M. Concussion incidence and recurrence in professional Australian football match-play: A 14-year analysis. J Sports Med (Hindawi Publ Corp). 2017;2017:2831751. DOI:10.1155/2017/2831751
Figure 3.8: Case control versus cohort studies. Kindred Grey. 2022. Includes person by Gan Khoon Lay from Noun Project (Noun Project License). Adapted under fair use from Song JW, Chung KC. Observational studies: Cohort and case-control studies. Plast Reconstr Surg. 2010;126(6):2234–2242. DOI:10.1097/PRS.0b013e3181f44abc
Figure 3.9: Example 2x2 table. Kindred Grey. 2022. CC BY 4.0.
Figure 3.10: Example of alternative 2x2 tables. Kindred Grey. 2022. CC BY 4.0.
Figure 3.11: The variety of measures that can be calculated from different study designs. Thiese MS. Observational and interventional study design types: An overview. Biochem Med (Zagreb). 2014;24(2):199–210. DOI:10.11613/BM.2014.022 (CC BY-NC-ND 3.0)
Figure 3.12: Interpreting odds ratios. Kindred Grey. 2022. CC BY 4.0.
Figure 3.13: Interpreting relative risks. Kindred Grey. 2022. CC BY 4.0.
Figure 3.14: Steps to solving an outbreak. Kindred Grey. 2022. CC BY 4.0. Adapted from CDC. Public Domain.
Figure 3.15: Example case definition. Kindred Grey. 2022. Adapted under fair use from Janka GE. Familial and acquired hemophagocytic lymphohistiocytosis. Annu Rev Med. 2012;63:233–246. DOI:10.1146/annurev-med-041610-134208 and Henter J-I, Horne A, Aricó M, et al. HLH-2004: Diagnostic and therapeutic guidelines for hemophagocytic lymphohistiocytosis. Pediatr Blood Cancer. 2007;48(2):124–131.
Figure 3.16: Example line listing. Data from table 6.5 of Lesson 6: Investigating an outbreak, from CDC. Public domain.
Figure 3.17: Example attack rate. Kindred Grey. 2022. CC BY 4.0.
Figure 3.18: Using a 2x2 table to calculate attributable risk. Kindred Grey. 2022. CC BY 4.0.
Figure 3.19: Calculating attributable risk. Kindred Grey. 2022. CC BY 4.0.
Figure 3.21: Graphical representation of figure 3.20. Kindred Grey. 2022. CC BY 4.0.
Figure 3.22: EXAMPLE NNH, NNT, ARR, RRR. Kindred Grey. 2022. CC BY 4.0. Data from Omi Y, Sugimoto D, Kuriyama S, et al. Effect of hip-focused injury prevention training for anterior cruciate ligament injury reduction in female basketball players: A 12-year prospective intervention study. Am J Sports Med. 2018;46(4):852–861. DOI:10.1177/0363546517749474
Figure 3.23: Calculating the population attributable risk using women’s basketball injuries. Kindred Grey. 2022. CC BY 4.0.
Figure 3.24: Standards for study design and reporting. Adapted under fair use from Thiese MS. Observational and interventional study design types: An overview. Biochem Med (Zagreb). 2014;24(2):199–210. DOI:10.11613/BM.2014.022 (CC BY-NC-ND 3.0)
- Which Came First—The Chicken or the Egg? https://www.youtube.com/watch?v=1a8pI65emDE. AsapSCIENCE via YouTube; 2013. ↵
- Gibbs N, Watsford M. Concussion incidence and recurrence in professional Australian football match-play: A 14-year analysis. J Sports Med (Hindawi Publ Corp). 2017;2017:2831751. ↵
- Rosling H. The best stats you've ever seen. https://www.youtube.com/watch?v=hVimVzgtD6w. TED via YouTube; 2006. ↵
- Martinez MW, Tucker AM, Bloom OJ, et al. Prevalence of inflammatory heart disease among professional athletes with prior COVID-19 infection who received systematic return-to-play cardiac screening. JAMA Cardiol. 2021;6(7):745–752. ↵
- Martinez MW, Tucker AM, Bloom OJ, et al. Prevalence of inflammatory heart disease among professional athletes with prior COVID-19 infection who received systematic return-to-play cardiac screening. JAMA Cardiol. 2021;6(7):745–752. ↵
- Centers for Disease Control and Prevention. Investigating an outbreak. In: Principles of epidemiology. 3rd ed: U.S. Department of Health and Human Services; 2006:6-1–6-78. ↵
- Centers for Disease Control and Prevention. Surveillance case definitions for current and historical conditions. https://ndc.services.cdc.gov/. Updated 2023. Accessed September 15, 2023. ↵
- Virginia Department of Health. Rules and regulations of the Board of Health, Commonwealth of Virginia. https://www.vdh.virginia.gov/surveillance-and-investigation/. Published 2021. Accessed 2021. ↵
- Centers for Disease Control and Prevention. Investigating outbreaks: Using data to link foodborne disease outbreaks to a contaminated source. https://www.cdc.gov/foodsafety/outbreaks/basics/data-types-collected.html?CDC_AA_refVal=https%3A%2F%2Fwww.cdc.gov%2Ffoodsafety%2Foutbreaks%2Finvestigating-outbreaks%2Findex.html. Published 2016. Accessed 2021. ↵
- Centers for Disease Control and Prevention. Morbidity and mortality weekly report. https://www.cdc.gov/mmwr/index.html. Published 2022. Accessed 2022. ↵
- Centers for Disease Control and Prevention. CDC WONDER. http://wonder.cdc.gov. Reviewed 2023. Accessed 15 September 2023. ↵
- Newcombe RG, Bender R. Implementing GRADE: Calculating the risk difference from the baseline risk and the relative risk. Evid Based Med. 2014;19(1):6–8. ↵
- Irwig L, Irwig J, Trevena L, Sweet M. Relative risk, relative and absolute risk reduction, number needed to treat and confidence intervals. In: Smart Health Choices: Making Sense of Health Advice.Hammersmith Press; 2008. ↵
- Omi Y, Sugimoto D, Kuriyama S, et al. Effect of hip-focused injury prevention training for anterior cruciate ligament injury reduction in female basketball players: A 12-year prospective intervention study. Am J Sports Med. 2018;46(4):852–861. ↵
- Omi Y, Sugimoto D, Kuriyama S, et al. Effect of hip-focused injury prevention training for anterior cruciate ligament injury reduction in female basketball players: A 12-year prospective intervention study. Am J Sports Med. 2018;46(4):852–861. ↵
- Reuters Fact Check. Fact Check: Why relative risk reduction, not absolute risk reduction, is most often used in calculating vaccine efficacy. 2023. https://www.reuters.com/article/factcheck-thelancet-riskreduction/fact-check-why-relative-risk-reduction-not-absolute-risk-reduction-is-most-often-used-in-calculating-vaccine-efficacy-idUSL2N2NK1XA. Accessed 15 September 2023. ↵
- The NNT Group. theNNT, explained. https://www.thennt.com/thennt-explained/. Accessed 15 September 2023. ↵
- Noordzij M, van Diepen M, Caskey FC, Jager KJ. Relative risk versus absolute risk: One cannot be interpreted without the other. Nephrol Dial Transplant. 2017;32(suppl 2):ii13–ii18. ↵
- Kim HY. Statistical notes for clinical researchers: Risk difference, risk ratio, and odds ratio. Restor Dent Endod. 2017;42(1):72–76. ↵
- EQUATOR network. Enhancing the QUAlity and Transparency Of health Research. https://www.equator-network.org/. Published 2023. Accessed 15 September 2023. ↵
- Broglio SP, McCrea M, McAllister T, et al. A national study on the effects of concussion in collegiate athletes and US Military Service Academy members: The NCAA-DoD Concussion Assessment, Research and Education (CARE) consortium structure and methods. N Zeal J Sports Med. 2017;47(7):1437–1451. ↵

